Generating a Quantum Galton board circuit using qmod #1225
Description
Introduction
Hello, we present our project on implementing a quantum algorithm for simulating a Galton Board (QGB) with exponential speedup. Our approach leverages a quantum circuit design that computes
Paper summary
A quantum circuit for simulating a Galton Board (GB) is introduced, demonstrating exponential speedup by computing 2n trajectories with
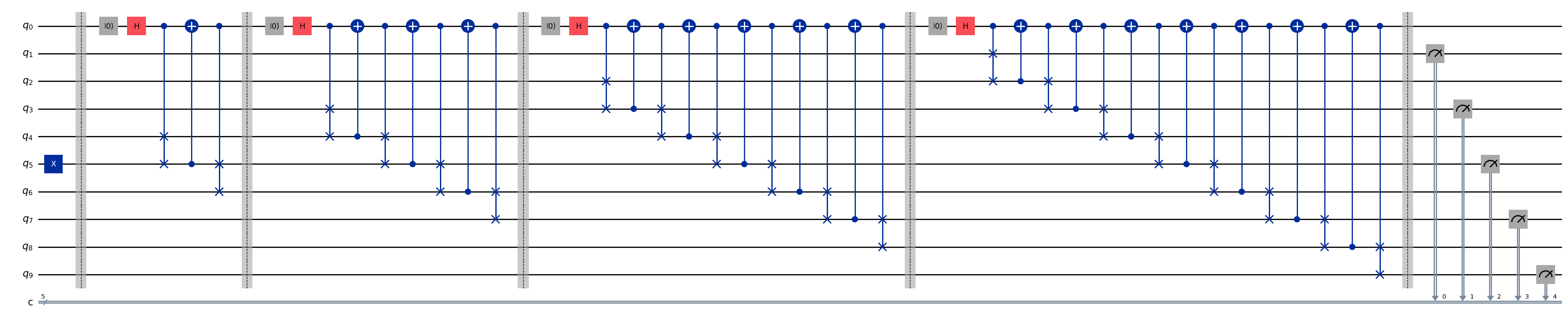
In the basic approach, qubits are initialized to |0⟩, with the middle qubit inverted via an X gate to represent the "ball". A control qubit is placed in superposition using a Hadamard gate. Controlled-SWAP operations are applied to simulate left or right deflections, followed by an inverted CNOT to stabilize the control qubit, and another SWAP to achieve the desired state, yielding a 50% probability split.
For scaling to an n-level Quantum Galton Board (QGB), the peg module is replicated successively, with mid-circuit resets on the control qubit and additional CNOTs to rebalance probabilities. An n-level QGB requires 2n qubits (n working, n ancilla) and up to
Biased QGBs are constructed by replacing Hadamard gates with Rx(θ) rotations, allowing control over deflection probabilities (e.g., 75%:25% via θ = 2π/3). Fine-grained per-peg bias is achieved through iterative application, incorporating extra resets and corrective CNOTs at row ends, resulting in approximately
Possible use case
Probability Distribution simulation: It enables simulation of various statistical distributions (e.g., Hadamar, Gaussian) by adjusting bias angles and peg configurations, useful in statistical modeling and Monte Carlo methods.
Implementation plan (qmod function)
def quantum_galton_board(layers, classical, global_bias, bias_angles=[]):
Parameters:
- layers: Number of Galton board layers
- classical: Boolean to indicate whether to add resets between layers
- global_bias: Angle to apply a global bias rotation to the circuit
- bias_angles: List of dictionaries specifying per-peg bias for each containing layer, peg position, and rotation angle
Example bias settings:
- Default bias angle = π/2
- Peg count = 50
- Specific biases:
- (layer 3, peg 6) → π/3
- (layer 4, peg 8) → 2π/3
Example output circuit:
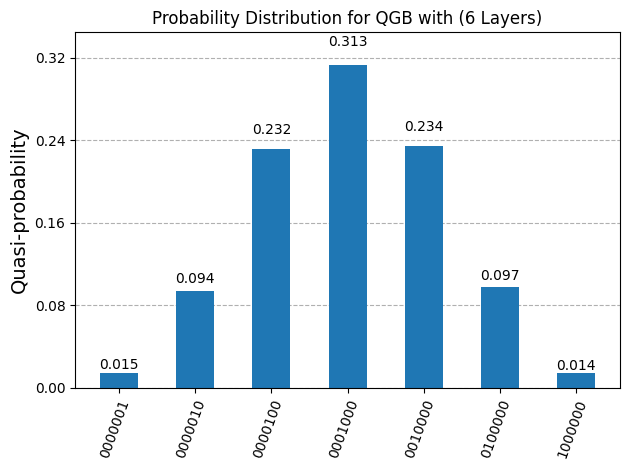
Simulation result:
