Numerically inconsistent

[ferrolho]

I would like to understand why I sometimes run into a numerical inconsistency.

For example, take a 3D shape defined by the following vertices:

vertices = [ -8.02  -2.955 -2.412
             -7.942 -2.622 -2.362
             -7.956 -1.271 -2.403
             -7.878 -0.937 -2.353
             -7.763  1.284 -2.392
             -7.685  1.617 -2.342
             -7.699  2.968 -2.383
             -7.621  3.301 -2.333
             -6.495  3.278 -1.779
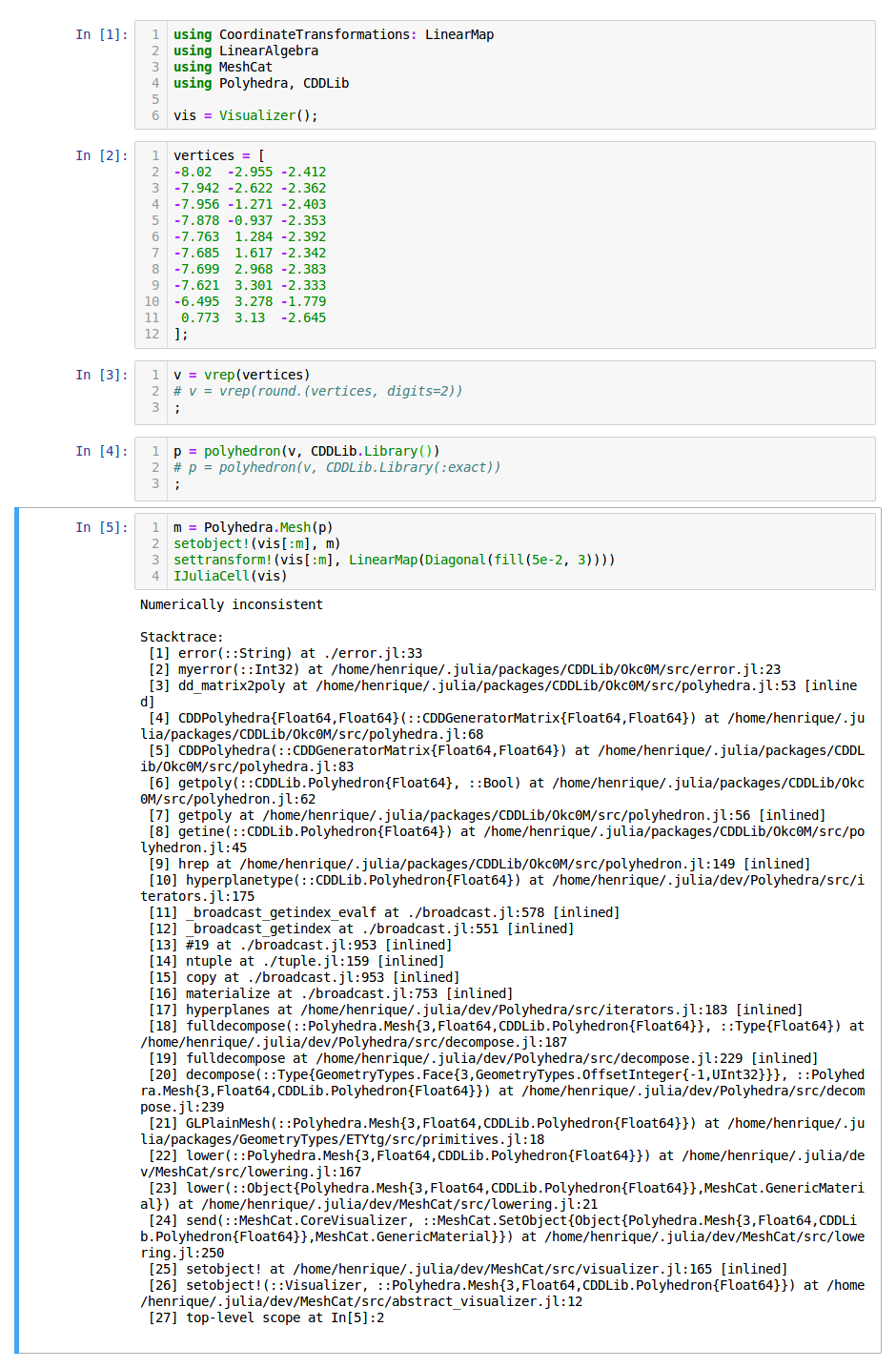
              0.773  3.13  -2.645 ]

Now, if I try to create a mesh from those vertices with

p = polyhedron(vrep(vertices), CDDLib.Library())
m = Polyhedra.Mesh(p)

I will end up with the following error:

Numerically inconsistent

Stacktrace:
 [1] error(::String) at ./error.jl:33
 [2] myerror(::Int32) at /home/henrique/.julia/packages/CDDLib/Okc0M/src/error.jl:23
 [3] dd_matrix2poly at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedra.jl:53 [inlined]
 [4] CDDPolyhedra{Float64,Float64}(::CDDGeneratorMatrix{Float64,Float64}) at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedra.jl:68
 [5] CDDPolyhedra(::CDDGeneratorMatrix{Float64,Float64}) at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedra.jl:83
 [6] getpoly(::CDDLib.Polyhedron{Float64}, ::Bool) at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedron.jl:62
 [7] getpoly at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedron.jl:56 [inlined]
 [8] getine(::CDDLib.Polyhedron{Float64}) at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedron.jl:45
 [9] hrep at /home/henrique/.julia/packages/CDDLib/Okc0M/src/polyhedron.jl:149 [inlined]
 [10] hyperplanetype(::CDDLib.Polyhedron{Float64}) at /home/henrique/.julia/dev/Polyhedra/src/iterators.jl:175
 [11] _broadcast_getindex_evalf at ./broadcast.jl:578 [inlined]
 [12] _broadcast_getindex at ./broadcast.jl:551 [inlined]
 [13] #19 at ./broadcast.jl:953 [inlined]
 [14] ntuple at ./tuple.jl:159 [inlined]
 [15] copy at ./broadcast.jl:953 [inlined]
 [16] materialize at ./broadcast.jl:753 [inlined]
 [17] hyperplanes at /home/henrique/.julia/dev/Polyhedra/src/iterators.jl:183 [inlined]
 [18] fulldecompose(::Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}}, ::Type{Float64}) at /home/henrique/.julia/dev/Polyhedra/src/decompose.jl:187
 [19] fulldecompose at /home/henrique/.julia/dev/Polyhedra/src/decompose.jl:229 [inlined]
 [20] decompose(::Type{GeometryTypes.Face{3,GeometryTypes.OffsetInteger{-1,UInt32}}}, ::Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}}) at /home/henrique/.julia/dev/Polyhedra/src/decompose.jl:239
 [21] GLPlainMesh(::Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}}) at /home/henrique/.julia/packages/GeometryTypes/ETYtg/src/primitives.jl:18
 [22] lower(::Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}}) at /home/henrique/.julia/dev/MeshCat/src/lowering.jl:167
 [23] lower(::Object{Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}},MeshCat.GenericMaterial}) at /home/henrique/.julia/dev/MeshCat/src/lowering.jl:21
 [24] send(::MeshCat.CoreVisualizer, ::MeshCat.SetObject{Object{Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}},MeshCat.GenericMaterial}}) at /home/henrique/.julia/dev/MeshCat/src/lowering.jl:250
 [25] setobject! at /home/henrique/.julia/dev/MeshCat/src/visualizer.jl:165 [inlined]
 [26] setobject!(::Visualizer, ::Polyhedra.Mesh{3,Float64,CDDLib.Polyhedron{Float64}}) at /home/henrique/.julia/dev/MeshCat/src/abstract_visualizer.jl:12
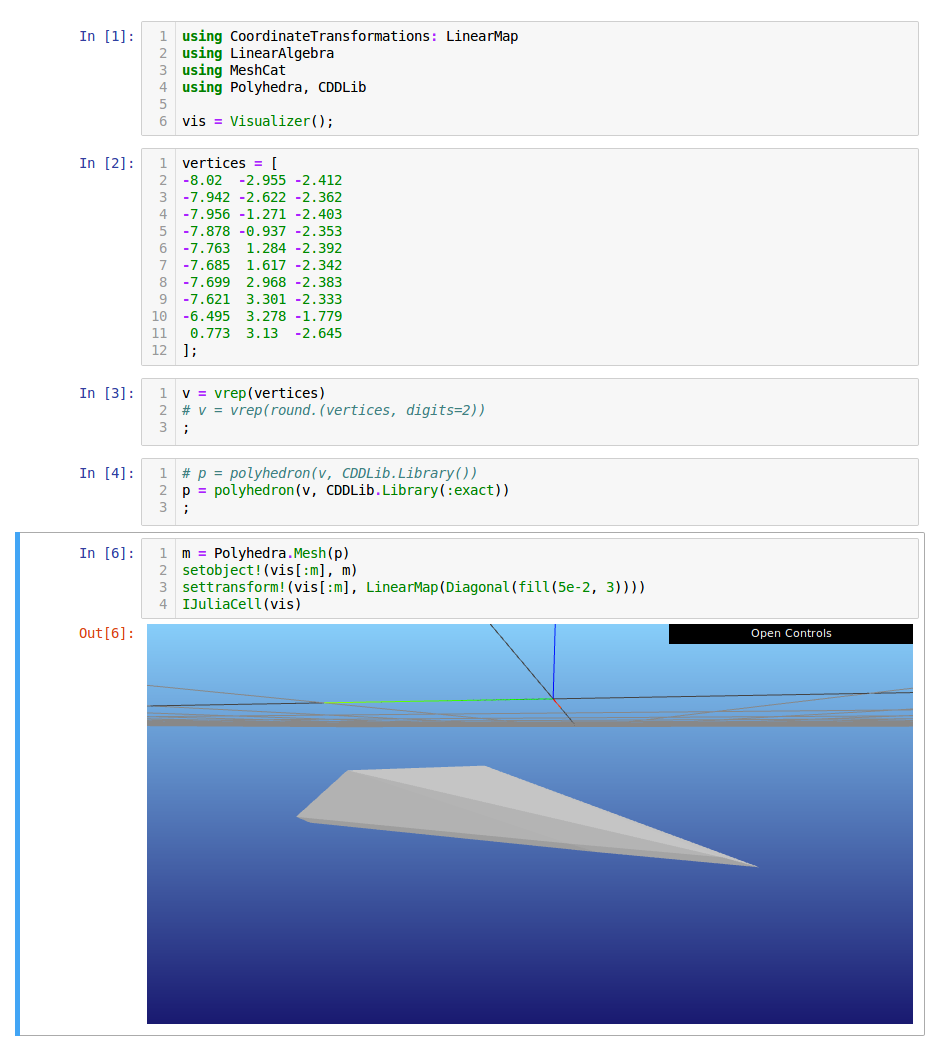
 [27] top-level scope at In[5]:2

Using exact arithmetic seems to get rid of this issue but at the cost of extreme computational times:

p = polyhedron(vrep(vertices), CDDLib.Library(:exact))
m = Polyhedra.Mesh(p)

---

Screenshots of a notebook showing both situations:

With exact arithmetic:

Without exact arithmetic:

[blegat]

It seems to be called from
https://github.com/cddlib/cddlib/blob/475890c3a760300f5b088c0c308d2b3b95b2acbb/lib-src/cddlib.c#L265
and
https://github.com/cddlib/cddlib/blob/475890c3a760300f5b088c0c308d2b3b95b2acbb/lib-src/cddlib.c#L303
It would be interesting to know what exactly causes that.

[ferrolho]

In https://github.com/cddlib/cddlib#numerical-problems they suggest playing with

#define dd_almostzero  1.0E-6

but I guess this would be quite difficult to change at the wrapper level compared to just recompiling cddlib.

[blegat]

You can compile it from source with a different constant and then copy the library in ~/.julia/packages/CDDLib/.../deps/usr/lib

[ferrolho]

@blegat, is the following statement still true? You have upstreamed your changes, haven't you?

CDDLib.jl/README.md

Lines 10 to 13 in 4fbfa40

	I needed to fork cddlib to write the wrapper because it is interface is text file based.
	My changes are not upstream yet, the version used by CDDLib.jl can be found [here](https://github.com/blegat/cddlib).

Also, if you are using any specific flags/options for the source compilation of cddlib, could you please enumerate and share those?

Thank you very much!

[blegat]

@blegat, is the following statement still true? You have upstreamed your changes, haven't you?

Indeed, this should be removed.
EDIT updated in 3d86b4c

Also, if you are using any specific flags/options for the source compilation of cddlib, could you please enumerate and share those?

The full script is:
https://github.com/JuliaPolyhedra/cddlibBuilder/blob/64ac358afe0b48aecb4f958c7c347b2ffbbe6cff/build_tarballs.jl#L18-L25

[ferrolho]

I am still trying to get to the bottom of this issue. I cannot figure out what is happening...

Below I compare the Julia output with the C output.

Here is the set of vertices I'll compare:

# Julia
vertices = [ -316.5    -109      -94.97
              245       228       79   
             -160       132.3    109   
             -377.3      63.6    -99.1
             -376.5      81.2    -93.4  ]

And for the C version, I created this test.ext:

V-representation
begin
5 3 real 
-316.5  -109    -94.97
 245     228     79   
-160     132.3  109   
-377.3    63.6  -99.1
-376.5    81.2  -93.4    
end

---

Julia notebook

Call to testcdd1.c

---

The Julia notebook throws the error here, when calling DDMatrix2Poly:

CDDLib.jl/src/polyhedra.jl

Lines 50 to 55 in c5c3633

	function dd_matrix2poly(matrix::Ptr{Cdd_MatrixData{Cdouble}})
	err = Ref{Cdd_ErrorType}(0)
	poly = @ddf_ccall DDMatrix2Poly Ptr{Cdd_PolyhedraData{Cdouble}} (Ptr{Cdd_MatrixData{Cdouble}}, Ref{Cdd_ErrorType}) matrix err
	myerror(err[])
	poly
	end

Which is what I find very weird and cannot understand, since testcdd1.c is calling that same function and does not fail: github.com/cddlib/cddlib/src/testcdd1.c#L67.

Any idea of what is going on?

---

Edit

OK, my bad for not even questioning the output of testcdd1.c. The output is obviously wrong as it takes more than 3 halfspaces to describe the V-rep passed as the input to the problem.

[blegat]

The test.ext should be

V-representation
begin
5 4 real 
1 -316.5  -109    -94.97
1 245     228     79   
1 -160     132.3  109   
1 -377.3    63.6  -99.1
1 -376.5    81.2  -93.4    
end

You need to transform it to a cone so you take the conic hull of the cartesian product of {1} with the polytope.

[ferrolho]

Ups... thanks! Indeed the output is now consistent with Julia's output:

➜  src git:(master) ✗ ./testcdd1    

>> Input file: /home/henrique/Downloads/cddlib/examples-ext/test1.ext
input file /home/henrique/Downloads/cddlib/examples-ext/test1.ext is open
size = 5 x 4
Number Type = real
*Error: Numerical inconsistency is found.  Use the GMP exact arithmetic.

[matbesancon]

Not sure if we should close this issue or not yet. Otherwise, I ran into another "numerical inconsistent" issue:
The polyhedron is defined as:

 HalfSpace([-1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0], 0.0)
 HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0], 0.0)
 HalfSpace([-0.0, -26.0, -0.0, -0.0, -50.0, -35.0, -0.0, -25.0, -23.0, -26.0, -0.0, -0.0, -46.0, -23.0, -18.0], 0.0)
 HalfSpace([-4.0, -42.0, -0.0, -29.0, -27.0, -5.0, -29.0, -25.0, -26.0, -24.0, -0.0, -26.0, -33.0, -0.0, -22.0], -37.0)
 HalfSpace([-13.0, -0.0, -45.0, -10.0, -7.0, -0.0, -27.0, -19.0, -25.0, -11.0, -0.0, -8.0, -17.0, -6.0, 3.0], -47.0)
 HalfSpace([-23.0, -0.0, -0.0, -0.0, -16.0, -44.0, -18.0, -3.0, -2.0, -0.0, -35.0, -45.0, -17.0, -5.0, -49.0], 0.0)
 HalfSpace([-43.0, -0.0, -47.0, -34.0, -37.0, -0.0, -37.0, -47.0, -33.0, -35.0, -0.0, -46.0, -2.0, -27.0, 34.0], -47.0)
 HalfSpace([-28.0, -11.0, -27.0, -25.0, -49.0, -0.0, -13.0, -0.0, -43.0, -11.0, -34.0, -23.0, -0.0, -33.0, 7.0], 0.0)
 HalfSpace([-33.0, -0.0, -0.0, -38.0, -39.0, -0.0, -6.0, -47.0, -0.0, -0.0, -20.0, -0.0, -0.0, -19.0, -29.0], 0.0)
 HalfSpace([-0.0, -0.0, -22.0, -0.0, -26.0, -0.0, -0.0, -37.0, -48.0, -21.0, -0.0, -38.0, -36.0, -40.0, 1.0], -9.0)
 HalfSpace([-41.0, -5.0, -30.0, -14.0, -10.0, -0.0, -0.0, -31.0, -9.0, -11.0, -0.0, -49.0, -0.0, -36.0, -36.0], -19.0)
 HalfSpace([-46.0, -4.0, -0.0, -31.0, -40.0, -36.0, -1.0, -22.0, -0.0, -21.0, -14.0, -0.0, -37.0, -34.0, 19.0], -1.0)
 HalfSpace([-15.0, -0.0, -42.0, -3.0, -19.0, -38.0, -24.0, -17.0, -35.0, -41.0, -0.0, -0.0, -5.0, -8.0, -44.0], 0.0)
 HalfSpace([-47.0, -0.0, -36.0, -0.0, -31.0, -0.0, -0.0, -6.0, -14.0, -8.0, -0.0, -20.0, -44.0, -0.0, -4.0], -35.0)
 HalfSpace([-5.0, -0.0, -9.0, -23.0, -21.0, -19.0, -8.0, -8.0, -5.0, -2.0, -0.0, -22.0, -22.0, -43.0, 1.0], -5.0)
 HalfSpace([-25.0, -0.0, -0.0, -11.0, -42.0, -0.0, -28.0, -46.0, -48.0, -37.0, -25.0, -38.0, -46.0, -19.0, -16.0], 0.0)
 HalfSpace([-36.0, -0.0, -21.0, -0.0, -2.0, -0.0, -0.0, -41.0, -1.0, -49.0, -19.0, -0.0, -32.0, -23.0, -30.0], 0.0)

Error:

julia> Polyhedra.vrep(poly)
ERROR: Numerically inconsistent
Stacktrace:
 [1] error(::String) at ./error.jl:33
 [2] myerror(::Int32) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/error.jl:23
 [3] dd_matrix2poly at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedra.jl:53 [inlined]
 [4] CDDLib.CDDPolyhedra{Float64,Float64}(::CDDLib.CDDInequalityMatrix{Float64,Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedra.jl:68
 [5] CDDLib.CDDPolyhedra(::CDDLib.CDDInequalityMatrix{Float64,Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedra.jl:83
 [6] getpoly(::CDDLib.Polyhedron{Float64}, ::Bool) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:60
 [7] getpoly at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:56 [inlined]
 [8] getext(::CDDLib.Polyhedron{Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:51
 [9] vrep(::CDDLib.Polyhedron{Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:156
 [10] top-level scope at REPL[106]:1

The same polyhedron defined with CDDLib.Library(:exact) works

[matbesancon]

For a more readable format, the polyhedron was created from the following JuMP model:

 cons[1] : 26 α[2] + 50 α[5] + 35 α[6] + 25 α[8] + 23 α[9] + 26 α[10] + 46 α[13] + 23 α[14] + 18 β ≥ 0.0
 cons[2] : 4 α[1] + 42 α[2] + 29 α[4] + 27 α[5] + 5 α[6] + 29 α[7] + 25 α[8] + 26 α[9] + 24 α[10] + 26 α[12] + 33 α[13] + 22 β ≥ 37.0
 cons[3] : 13 α[1] + 45 α[3] + 10 α[4] + 7 α[5] + 27 α[7] + 19 α[8] + 25 α[9] + 11 α[10] + 8 α[12] + 17 α[13] + 6 α[14] - 3 β ≥ 47.0
 cons[4] : 23 α[1] + 16 α[5] + 44 α[6] + 18 α[7] + 3 α[8] + 2 α[9] + 35 α[11] + 45 α[12] + 17 α[13] + 5 α[14] + 49 β ≥ 0.0
 cons[5] : 43 α[1] + 47 α[3] + 34 α[4] + 37 α[5] + 37 α[7] + 47 α[8] + 33 α[9] + 35 α[10] + 46 α[12] + 2 α[13] + 27 α[14] - 34 β ≥ 47.0
 cons[6] : 28 α[1] + 11 α[2] + 27 α[3] + 25 α[4] + 49 α[5] + 13 α[7] + 43 α[9] + 11 α[10] + 34 α[11] + 23 α[12] + 33 α[14] - 7 β ≥ 0.0
 cons[7] : 33 α[1] + 38 α[4] + 39 α[5] + 6 α[7] + 47 α[8] + 20 α[11] + 19 α[14] + 29 β ≥ 0.0
 cons[8] : 22 α[3] + 26 α[5] + 37 α[8] + 48 α[9] + 21 α[10] + 38 α[12] + 36 α[13] + 40 α[14] - β ≥ 9.0
 cons[9] : 41 α[1] + 5 α[2] + 30 α[3] + 14 α[4] + 10 α[5] + 31 α[8] + 9 α[9] + 11 α[10] + 49 α[12] + 36 α[14] + 36 β ≥ 19.0
 cons[10] : 46 α[1] + 4 α[2] + 31 α[4] + 40 α[5] + 36 α[6] + α[7] + 22 α[8] + 21 α[10] + 14 α[11] + 37 α[13] + 34 α[14] - 19 β ≥ 1.0
 cons[11] : 15 α[1] + 42 α[3] + 3 α[4] + 19 α[5] + 38 α[6] + 24 α[7] + 17 α[8] + 35 α[9] + 41 α[10] + 5 α[13] + 8 α[14] + 44 β ≥ 0.0
 cons[12] : 47 α[1] + 36 α[3] + 31 α[5] + 6 α[8] + 14 α[9] + 8 α[10] + 20 α[12] + 44 α[13] + 4 β ≥ 35.0
 cons[13] : 5 α[1] + 9 α[3] + 23 α[4] + 21 α[5] + 19 α[6] + 8 α[7] + 8 α[8] + 5 α[9] + 2 α[10] + 22 α[12] + 22 α[13] + 43 α[14] - β ≥ 5.0
 cons[14] : 25 α[1] + 11 α[4] + 42 α[5] + 28 α[7] + 46 α[8] + 48 α[9] + 37 α[10] + 25 α[11] + 38 α[12] + 46 α[13] + 19 α[14] + 16 β ≥ 0.0
 cons[15] : 36 α[1] + 21 α[3] + 2 α[5] + 41 α[8] + α[9] + 49 α[10] + 19 α[11] + 32 α[13] + 23 α[14] + 30 β ≥ 0.0
 α[1] ≥ 0.0
 α[2] ≥ 0.0
 α[3] ≥ 0.0
 α[4] ≥ 0.0
 α[5] ≥ 0.0
 α[6] ≥ 0.0
 α[7] ≥ 0.0
 α[8] ≥ 0.0
 α[9] ≥ 0.0
 α[10] ≥ 0.0
 α[11] ≥ 0.0
 α[12] ≥ 0.0
 α[13] ≥ 0.0
 α[14] ≥ 0.0
 β ≥ 0.0

[sebastiendesignolle]

I also run into numerical inconsistency and want to play with the value of dd_almostzero. I've cloned cddlib and modified cdd.h accordingly, but, after placing the entire cddlib folder in ~/.julia/packages/CDDLib/.../deps/usr/lib as explained above, the new library is not loaded. What shall I do to indicate CDDLib.jl where to find it?

[matbesancon]

@sebastiendesignolle I think this was with an old build system. With the new one, you should override the artifact location for cddlib_jll:
https://pkgdocs.julialang.org/v1/artifacts/#Overriding-artifact-locations

[matbesancon]

The UUID to override is here:
https://github.com/JuliaBinaryWrappers/cddlib_jll.jl/blob/main/Artifacts.toml
So this one: d404927e6c241215ee2871ba75c33e56548a63f0 I think

[matbesancon]

in a file .julia/artifacts/Overrides.toml