diff --git a/recognition/MySolution/s47539934-GCN/Accuracy.png b/recognition/MySolution/s47539934-GCN/Accuracy.png
new file mode 100644
index 0000000000..d2c94b2add
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/Accuracy.png differ
diff --git a/recognition/MySolution/s47539934-GCN/Data.py b/recognition/MySolution/s47539934-GCN/Data.py
new file mode 100644
index 0000000000..302d946232
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/Data.py
@@ -0,0 +1,51 @@
+'''
+Author name: Arsh Upadhyaya, s47539934
+To preprocess dataset facebook.npz
+'''
+
+import numpy as np
+from sklearn import preprocessing
+import torch
+import scipy.sparse
+import torch.nn.functional as F
+import matplotlib.pyplot as plt
+import scipy.sparse as sp
+import torch.optim as optim
+
+
+def load_data(file_path):
+ '''
+ parameters:
+ takes file path
+ returns:
+ Adjacency matrix: normalized coo matrix
+ features and labels(targets) as tensors
+ '''
+
+ data = np.load("/content/drive/MyDrive/facebook.npz")
+ edges = data['edges']
+ features = data['features']
+ labels = data['target']
+
+ features = sp.csr_matrix(features)
+
+ adj= sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),shape=(labels.shape[0], labels.shape[0]))
+
+ #normalize
+ colsum = np.array(adj.sum(0))
+ D = np.power(colsum, -1)[0]
+ D[np.isinf(D)] = 0
+ D_inv = sp.diags(D)
+ adj_trans = D_inv.dot(adj)
+
+ #transform data type
+ indices = torch.LongTensor(np.vstack((adj_trans.tocoo().row, adj_trans.tocoo().col)))
+ values = torch.FloatTensor(adj_trans.data)
+ shape = adj_trans.shape
+
+ adj_trans = torch.sparse_coo_tensor(indices, values, shape)
+ features = torch.FloatTensor(np.array(features.todense()))
+ labels = torch.LongTensor(labels)
+
+ return adj_trans, features, labels
+
diff --git a/recognition/MySolution/s47539934-GCN/GCN_final.ipynb b/recognition/MySolution/s47539934-GCN/GCN_final.ipynb
new file mode 100644
index 0000000000..1bfab0bd5e
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/GCN_final.ipynb
@@ -0,0 +1,648 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "provenance": [],
+ "authorship_tag": "ABX9TyOdKktAKTsIX4iuqCL4y12Z",
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ },
+ "language_info": {
+ "name": "python"
+ },
+ "accelerator": "GPU"
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 35
+ },
+ "id": "4Tpyn_NtoRSE",
+ "outputId": "927e952a-8a55-4448-b8f2-fbd1a0fb6b4d"
+ },
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "'\\nAuthor name: Arsh Upadhyaya\\nRoll no. s4753993\\nCode for 2 layer GCN\\n'"
+ ],
+ "application/vnd.google.colaboratory.intrinsic+json": {
+ "type": "string"
+ }
+ },
+ "metadata": {},
+ "execution_count": 1
+ }
+ ],
+ "source": [
+ "'''\n",
+ "Author name: Arsh Upadhyaya\n",
+ "Roll no. s4753993\n",
+ "Code for 2 layer GCN\n",
+ "'''"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "from google.colab import drive"
+ ],
+ "metadata": {
+ "id": "jsqqEDjjqjZi"
+ },
+ "execution_count": 2,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "drive.mount('/content/drive')"
+ ],
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "p_dNPCQKrVqa",
+ "outputId": "b49f52ea-d538-45b0-9ebf-de7ab4d024fe"
+ },
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Mounted at /content/drive\n"
+ ]
+ }
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "import math\n",
+ "import torch.nn.init as init\n",
+ "import numpy as np\n",
+ "import scipy.sparse as sp\n",
+ "import torch\n",
+ "import torch.nn as nn\n",
+ "import torch.nn.functional as F\n",
+ "from torch.nn.parameter import Parameter\n",
+ "from torch.nn.modules.module import Module\n",
+ "import torch.optim as optim\n",
+ "from random import sample\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "metadata": {
+ "id": "V2CFruE7r4yV"
+ },
+ "execution_count": 4,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def load_data(file_path):\n",
+ " \n",
+ " data = np.load(\"/content/drive/MyDrive/facebook.npz\")#path of file through google drive\n",
+ " edges = data['edges']\n",
+ " features = data['features']\n",
+ " labels = data['target']\n",
+ "\n",
+ " features = sp.csr_matrix(features)\n",
+ "\n",
+ " adj= sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),shape=(labels.shape[0], labels.shape[0]))\n",
+ "\n",
+ " #normalize\n",
+ " colsum = np.array(adj.sum(0))\n",
+ " D = np.power(colsum, -1)[0]\n",
+ " D[np.isinf(D)] = 0\n",
+ " D_inv = sp.diags(D)\n",
+ " adj_trans = D_inv.dot(adj)\n",
+ "\n",
+ " #transform data type\n",
+ " indices = torch.LongTensor(np.vstack((adj_trans.tocoo().row, adj_trans.tocoo().col)))\n",
+ " values = torch.FloatTensor(adj_trans.data)\n",
+ " shape = adj_trans.shape\n",
+ "\n",
+ " adj_trans = torch.sparse_coo_tensor(indices, values, shape)\n",
+ " features = torch.FloatTensor(np.array(features.todense()))\n",
+ " labels = torch.LongTensor(labels)\n",
+ "\n",
+ " return adj_trans, features, labels"
+ ],
+ "metadata": {
+ "id": "KDdp_bTnru0h"
+ },
+ "execution_count": 5,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "\n",
+ "\n",
+ "\n",
+ "class GraphConvolution(Module):\n",
+ " '''\n",
+ " Starting of graph convolutional layer.\n",
+ " Parameters:\n",
+ " input_features: dimensions of input layer\n",
+ " output_features: dimenstions of output layer\n",
+ " use_bias: optional but good practice\n",
+ " '''\n",
+ "\n",
+ " def __init__(self, in_features, out_features, use_bias=True):\n",
+ " super(GraphConvolution, self).__init__()\n",
+ " self.in_features = in_features\n",
+ " self.out_features = out_features\n",
+ " self.use_bias=use_bias\n",
+ " self.weight = Parameter(torch.FloatTensor(in_features, out_features))\n",
+ " if self.use_bias:\n",
+ " self.bias = Parameter(torch.FloatTensor(out_features))\n",
+ " else:\n",
+ " self.register_parameter('bias', None)\n",
+ " self.reset_parameters()\n",
+ " #initialize parameters \n",
+ " def reset_parameters(self):\n",
+ " self.weight = nn.init.kaiming_uniform_(self.weight)\n",
+ " if self.use_bias:\n",
+ " init.zeros_(self.bias)\n",
+ "\n",
+ "# parameters:\n",
+ "# in_feature: an n-dimenstional vector\n",
+ "# adj_matrix: an adjacency matrix in tensor format\n",
+ "\n",
+ " def forward(self, input, adj):\n",
+ "\n",
+ " support = torch.mm(input, self.weight) \n",
+ " output = torch.sparse.mm(adj, support)\n",
+ "\n",
+ " return output\n",
+ "\n",
+ "\n",
+ "class GCN(nn.Module):\n",
+ "\n",
+ "# A model that contains 2 layers of GCN , by creating 2 instances from GraphConvolution function\n",
+ "# parameters:\n",
+ "# in_feature:n dimensional vector, which is input\n",
+ "# out_class: n dimensional vector, final output\n",
+ "# in this case model goes 128->32->4\n",
+ "# since in_feature=128(known from dataset)\n",
+ "# out_class=4(since finally 4 classes)\n",
+ "\n",
+ " def __init__(self, in_feature, out_class, dropout):\n",
+ " super(GCN, self).__init__()\n",
+ "\n",
+ " self.gcn_conv_1 = GraphConvolution(in_feature, 32)#32 is like the hidden layer for the overall model\n",
+ " self.gcn_conv_2 = GraphConvolution(32, out_class)\n",
+ " self.dropout = dropout\n",
+ "\n",
+ " def forward(self, x, adj):\n",
+ " x = F.relu(self.gcn_conv_1(x, adj))\n",
+ " x = F.dropout(x, self.dropout, training=self.training)\n",
+ " x = self.gcn_conv_2(x, adj)\n",
+ "\n",
+ " return F.log_softmax(x, dim=1)"
+ ],
+ "metadata": {
+ "id": "dZwEJTIVt9-C"
+ },
+ "execution_count": 6,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def accuracy(output, labels):\n",
+ " '''\n",
+ " calculate accuracy\n",
+ " parameters: \n",
+ " output:result of running an instance of the model\n",
+ " labels: the true value\n",
+ " function compares ratio of two values, giving result<1, \n",
+ " as predicted probability always less than true value\n",
+ " '''\n",
+ " predict = output.argmax(1)\n",
+ " acc_ = torch.div(predict.eq(labels).sum(), labels.shape[0])\n",
+ " return acc_"
+ ],
+ "metadata": {
+ "id": "qsMqOqxTwjd9"
+ },
+ "execution_count": 7,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def loss(output,labels):\n",
+ "\n",
+ " prab = output.gather(1, labels.view(-1,1))\n",
+ " loss = -torch.mean(prab)\n",
+ " return loss"
+ ],
+ "metadata": {
+ "id": "WUessmBVwpQb"
+ },
+ "execution_count": 8,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def train_model(n_epochs):\n",
+ " '''\n",
+ " parameter: number of epochs\n",
+ " trains model over the range of the epoch and at each train, \n",
+ " calculates accuracy and losses\n",
+ " '''\n",
+ " train_losses=[]\n",
+ " validation_losses=[]\n",
+ " train_accuracies=[]\n",
+ " validation_accuracies=[]\n",
+ " for epoch in range(n_epochs):\n",
+ " model.train()\n",
+ " optimizer.zero_grad()\n",
+ " output=model(features,adj)\n",
+ " train_loss=loss(output[train_set],labels[train_set])\n",
+ " train_losses.append(train_loss.item())\n",
+ "\n",
+ " train_accuracy=accuracy(output[train_set],labels[train_set])\n",
+ " train_accuracies.append(train_accuracy.item())\n",
+ " train_loss.backward()\n",
+ " optimizer.step()\n",
+ " output=model(features,adj)\n",
+ " validation_loss=loss(output[val_set],labels[val_set])\n",
+ " validation_losses.append(validation_loss.item())\n",
+ " validation_accuracy=accuracy(output[val_set],labels[val_set])\n",
+ " validation_accuracies.append(validation_accuracy.item())\n",
+ " print('Epoch: {:04d}'.format(epoch + 1),\n",
+ " 'Train loss: {:.4f}'.format(train_loss.item()),\n",
+ " 'Train accuracy: {:.4f}'.format(train_accuracy.item()),\n",
+ " 'Validation loss: {:.4f}'.format(validation_loss.item()),\n",
+ " 'Validation accuracy: {:.4f}'.format(validation_accuracy.item()))\n",
+ " \n",
+ " np.save('train_losses', train_losses)\n",
+ " np.save('train_accuracies', train_accuracies)\n",
+ " np.save('validation_losses', validation_losses)\n",
+ " np.save('validation_accuracies', validation_accuracies)\n"
+ ],
+ "metadata": {
+ "id": "1tJrfwlHw2bC"
+ },
+ "execution_count": 9,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def test_model():\n",
+ " output=model(features,adj)\n",
+ " test_loss=loss(output[test_set],labels[test_set])\n",
+ " test_accuracy=accuracy(output[test_set],labels[test_set])\n",
+ " print('Test set results:',\n",
+ " 'Test loss: {:.4f}'.format(test_loss.item()),\n",
+ " 'Test accuracy: {:.4f}'.format(test_accuracy.item()))"
+ ],
+ "metadata": {
+ "id": "dnk6qMppxA1h"
+ },
+ "execution_count": 10,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ " adj, features, labels = load_data('facebook.npz')#returns normalized adjacency matrix, tensor features and labels\n",
+ " features.shape[0]\n",
+ " num_nodes=features.shape[0]\n",
+ " #split data in semi supervised quatity, i.e train:set:test=20:20:60(since n_train"
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD4CAYAAAD8Zh1EAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3deXxU1fnH8c8hBMK+xsi+iQoBwhIRRRbFBVFBURQqVnBrUSou1aJYRW1/1dYqYt2oWtGiFFEULUJtWUQFJWwKwQUSlrCEJBAgsibz/P54ZshC9kwymZnn/XrNKzN37tx5cjP5zplzzz3jRARjjDHBr0agCzDGGOMfFujGGBMiLNCNMSZEWKAbY0yIsEA3xpgQUTNQT9y8eXNp3759oJ7eGGOC0urVq9NFJLqw+wIW6O3btychISFQT2+MMUHJObetqPusy8UYY0KEBboxxoQIC3RjjAkRFujGGBMiLNCNMSZEWKAbY0yIsEA3xpgQYYFujDF+tHQpzJsHgZiZ3ALdGBNQ33wDixZBdnagK1EHD8KYMfDSS+DxFL7O0aMwYQL89a/5g3vpUrjsMhg5Evr3h++/P/WxBw5AVlallB64M0WNMaHJ44EapWgqHjwIEyfC22/r7ZgYuPJKGD0aLr64+MeKwHffQceOUL8+pKZCgwZQt27u/Zs2wRdfQGQkDBwInTrp7QkToGlTaNYM9u6FnBw4/XS45hoN4YkTYeFCmD0b/vQn2L8fGjaEc86B11+H2rU1sP/7X32u1at1O6mpkJysz3P33fD730N8vP6MjYVPPoHPPoOkJN3OLbeUfx8Xs2MkIJc+ffqIMSZwliwRufVWkW+/zb983TqRc88VWbMmd9lf/iIyaZKIx1P8NrdtE2nbVmTKlMLvT0wUGTdOZM4ckfh4kZo1dd0PPhC57jqRhg1FQOSyy0T++1+RH34QeeklkdRUkcOHRcaPF7nqKpHevXW9rl1Fnn9epE4dkZgYkSefFJk+XeS88/T+vJfLLxdp0ECkfXu9v2tXkQsvFLn0UpE2bfKv++qrIm+8ITJypP7e48aJREWJxMaKdOokUqOGyD/+IXL33br+2WeLXHONyA03iGzdqr/rjh0iAwfmbrNOHV3nj38U+e678v7VRIAEKSJXLdCNqSL795cciBWVnCxy1lkabEU915EjIo89pqEE+nPqVF3f48kNoU6dRDIzRT7/XMQ5Xfb66yLPPCMyapQG54YNGuKvviry4Yci55yTG2CvvSbyy19qMPpqa9ky9/6oKJFPPslf27FjIs8+K9KkSf6AjY/XUAWRuDi9PXWqSOPGuuyCC0QGD85dv317DfoffxTZuFHkiSdEGjUS6dhRJCXl1H2SkyOSkKC/x/vvF77fPvtMa27XTmTZstzlBw4Uva89Hn2+xYt1PX+wQDcmwDZuFKldW2TChPz//FlZIkOHisyYIXL0qMiNN4pMnqzLRUQWLtQQmjlT5MQJbbHOmyfy3HMif/5z/pDIyREZNCg3qIcO1XDcuTN3nWXLNJBAn2vbNpGxY/X2ww+LvPyyXr/1Vm09n3WWSOvWIh06aGj6AvO0005tAfsu77wj0qWLXve9Edx4oz6mcWNt+c+bJ7JqVdH768gRkdmzRV54Qd8QfNv53e/yr/fjjyIvvihy/Lju1717RXbvFsnOPnWbWVm5+7W8duwQOXSoYtuoKAt0Y8rhxImi79uyRVufiYkaPgsXinz0kcjq1RouCxZoEK1dq0Fz/fW5gXflldrCfOYZkTvv1GURESKXXJK7Ttu2IosWaYs2MlKX1ax5anhee21uy/r3v89tRT/1lEiLFnq7Xj2R3/5W5E9/EqlVS+TMM7U7wycnR+Tmm3O32aWL/u5z5mirNyZGZOlSkaQk7Yp55RV9vqQkbYX/9a/6hvX557nb3bRJ69m+XWTMGN3uJZfo/iiP114Tuekm3bfhzgLdhJWcHA3Dr78u/P5jx0SWL8/fchXRlt2QISJvviny/fcaZPffX/g2fvGL3LD0Bafv4gtg32XQIP350EManHXqiHTvnnv/HXdoSxi0P/mLL7TLwBf0X3+trdAHHtDavvlGJD1dQxtEfvUrkREj9PpNN+X/BPDjjxr6vhZu//4iGRmF77Ply7XbZPv28uz1ovm6HYx/FBfoTu+vevHx8WLzoRt/++wzuOceSEzU20OG6BCxmjWhd29IS9PRCenpen/DhjoK4rrrICFBRyw4pyMuUlM1chcsgKFD4S9/gbfegqlT4YYb4KabYM8eXefuu3WkRGIirFoFF14IXbroyIbHHoOICNi6FZo0yR0F8uyz8OWXMGuWbufTT+HXv9b70tN1tMV558GkSYX/rh6P1j1vno68eOwxmDxZ6y/oyBHYuRM6dNBaTPByzq0WkfhC7ytNoDvnhgLPAxHAayLyVIH72wFvANHAPmCsiKQUt00L9PCUmqrh07hx0evMmKHjkkeM0OCsXVuX5+To4+vWhVdfhQ8+gEOH4NJL4bbb4JlnYOZMOPNMePRRHUL2xhvQti0cOwbr12voxsfDqFGQkqIhm5EBc+ZoQP7rXzr++MsvNcgnTdJhZu3a6TC4OnU0HGvV0u23bFny77xjh76pdOnil12Yj4jWU6dO4UFuQk9xgV5i1wga4luAjkAtYD3QtcA67wE3e69fBLxd0natyyV8zJmj3QaHDom0aqUH+dLT9b6dO7UrYs8evb1smXYz1KmjXQSDB2v/7NSpenAub1fG+eeLDBuW251Qq5YeNDt8uOw1bt2qXRki2n/sq2fzZpHbbxe56CI9wLh9u0ifPqcenDNVbNs2fQE8/nj5hw4tWKB9W599ln/51q16RPmDDwp/3KpVInfdVfZhK2+9JfLoo9q/VQFUpA8dOA9YlOf2Q8BDBdbZCLTxXnfAwZK2a4EefObNE/nDH0T27SvbY0CHjPkOvEVGar/ya69pwPuCe9067Y/u3FmHy82cmb8/+tJLdajcH/+o/cw+q1bpAb9t2/z9G4eRo0c12IoLG49Hd/yRI0Wvc/iwjkUsqSP+6NGi33kzMvQAwcaNp953/LgegW7TRt/5QQ8gXHWVjk0sOIzFd8S44PXXX899fK9eunzxYh1W4zsoUqeOtkbGjtXB6AsX6gvaN1h+6FAdsvPMMyLTpulYzpYt9UDI+++LPPKIvig9Hh0nmvegSQXGr1Y00K9Du1l8t28C/lZgnXeASd7rIwEBmhWyrTuABCChbdu25f6FTOXzeERWrNADiMePizz4YO7rsXFjbaEuWqQjHpKTNYDHjdOgHjVKD8YtXaoncvTqJdK0qT72F7/QA3u+oXWtW+eOznBOD0TmPdFl6VJthCUlBWpPlNOJE7rzSuvIEd1pIvrzwQc1PIv7xy/NR5HU1PzDdf75Tx1iU3AA+IQJ+kd4/vnCt+PxiNx3n65zzjka/tOm6bLf/17PlJkyJTfs6tfXcZVffKHhnVdWlp6hU6OGHg2++GKRK67QI9K//KW+CHxHhH/1Kw3211/XdRo10vtiYjRMH3hApG5dHboDIs2ba7jfe6/Ib36j6w0cqMOSzj1X3wiuvlpODrt54YXc674XeLt2+vv5Bs03bKhjTn33n3GGDvQvOOSoWbP82wF9viuu0Ovjx+s/DuibQDlVRaC3BD4A1qJ97SlA4+K2ay306mXfPs0RXwPt7bfl5BC2Xr30+q9/ra3ha6/NDWTQ0D7rLB1WN3Cg/s/5Wtbt2mlj7X//0/t8Dbf0dB1T/fPPevuBB7ShtXt3QH790klOFnn66ZLHzu3eracyRkfraY5bt+bu2Jdf1hbfzz/rqZq33679SW3byslhLnlPWxw8WMf6TZyoQXXLLfoY3x/lyiuLPu3wn//UP0psrMjcudrFEBmZG069euUffN6okZ458/33Wu/Ysfo7xMbmDsO5+moN67ynP/pauqDv5h9+mD/YunXTcYw+t9yi796TJumpmP366f467zwN0X79tLV81135P6KdcYb+7vPm5X8z873pLV+uA967dtWQr1lTW9GRkfqCrV1bX4Q1augb0YkTeuncWbf/m9/kH8S+dq22JtLTtXtlyRJ9I/R9RH31VX1D2L1bJC0t93Wxdq3W/803+gYTGalvfr5PCNOn61lm5VTpXS4F1q8PpJS0XQv0qvWf/+jp1G+/fWrDcc2a3BZ006b6/9K2rf4Pt2+vjZyC3YnbtumY47VrRQYM0FD/z3/0vp07tbX+5JO5gR0wHo+2FB9/PLel6vGI/PRTbhD88IOGmK8rYft2Pbtn8GA9X/yhh3T9s8/WnfToo7nbf+UVDYI33tCd8vHHutPq1tVg8oVRq1YaRr7b/fppwERF6e24uNyxhw0bajj97W+6Hd8g9O7dNfBOP13D7+679eNS3bq687/5Rt8Z8wbweefpKZ++5+3USQ8QPP+8ninkC+MzztADBk2b6rvw+PG6fORIvYwYoW9mvgHo8+aJ7Nqlt3fs0MBauTL/fv/pJ31Tad5c3wRWrNAQ9L1xlUZKirZmly4tezeFL5gXLNA3r8WL9XbBEwzWrhV5993KOY03JUVfW35U0UCvCSQBHfIcFI0tsE5zoIb3+h+BJ0rargV61cnI0FD2nZhy1VW67Lzz9Oy9Bg20UfjKKyI9e+b+76987Ts5fiS72C5TEf0/qFBwb9umAfrwwyIHDxa+ztKl2jravDl32bFj2n0wduypH+t9fIO1fa3dp57SdyDQgPryy9yjqtHRGkBt2+rO6ttXg8AXer6PIBERGl5ffaWPzdtCBT3q+/XXumO+/FJ37Pnn5+5838f8Xr30D5GZqS3inByRv/9dz07y2bBBzwrydccUtHt3/kHtNWtq63jUKA33o0d1Py1erHUU7Nvev1/D2bdfv/km91TS8eP9E3I7dugbScOG2jq+/PLiz9oyxapQoOvjGQb86B3tMsW77AlguPf6dcBP3nVeA2qXtE0LdP95/HH9Hyl4SvLDD2u3Xmys/p/7jt+AHveJjNRPqNdck9tHnZmpLfmnBn+qK150UW4/yIkT2rI7/XRt0eSVk6NhsHatfkTNzCw8DFJTtRX78svaLzpmjAZiRISGY7t2GpQ+Ho+2kPMG5vXX65vAK6/kLuvaVQPy1lu1X2jKFF0G+hyvv57bVdCihb4R1Kmjfa9t2ugIBN/56o0a5Q/VTZu08//ttzUA27TRM4rattXrmZna7fHsszpjU2FdMh6PHvX13ff110W/eZVVRoYegHvzzbIdsS7Kvn36xlLSO3lZbNminy4uuKAafGwLbhUO9Mq4WKCX3YIF+ok1bw74GomgQ/h83SkzZsjJ41fNm+soEBHNlVvGHJY+rJJ//MO7kcREbUkuWaJh6PFoX2mjRhp6rVppC9l3ymP9+tqa9YXHvHmnni4J2k/pc+iQHjzzjUf0XRo21NMxt23TGjp21Heav/1N30B83RS3366t4kce0TBt1Uov/fqJzJqlfbAXX6xjF0FbgkOGaFeAb6f4PkpkZ2tL1Rfw8+fr/QcP6ptHcZOMiGiLc8gQfey//13+P2i4OXy48ElWTJlYoAeh3bu1Ydm6tZ7OnZiY291av74eOL/3Xu36bNMmt+UdHZ3bbTJ8SJacWLJcW27vvntyMHjOoMG6wqJFuR//817uv19bzA8+mDuWEDQs33xTl9WooV0dX32lfbg9e2p3xZw5GqLDhmkwb9miszX5tnHDDTryISVFPxYUHGaWkaEHsnwjGUA/auRt7a9fn3vfokX5H79li74ZJCeXvJM//FDHQJZHTo7/z5E3phQs0IPEwYMi772nWTFunOanL9saNNDjXx9/rMNYzz5bgz3mNM/J8yIWLtTjV4POPSI/xl0rHl9rNe8lKkqb9M2ba3dDgwbarbJwobbQr702d11fv+3WrRreX36ZW+zkybnrtWhx6vCUlBR9Lt+kJH375u9KKY7Ho10XnTrpm0NhkpK0C6Sy56M1ppqxQK+mCmbRpEn6F7n1Vm0gT5qky3XoqkdWj/qTnjzhGwK3cKF2WYwdq+8EDz2kHeW+8cJ3360HEn/4QQ+uvfOOyOjRGoS+M35q1cp/wC0rS8frDh9ecvFffqnjl4vqovANXr/zTjsIZoyfFBfoNjlXgBw97GHl6VeTdsU4Rr07koMHoXVrbfJmZUFcrU2svPAhojatRTp35lCbWBq+OV0ffO21+n1YU6fq5CS7d+tkJaAzTWVn6yxPL71UdAEiOotVjx5w662n3peTozNaVUR2NqxbB3362EQjxvhJhSfnqgzhHugL/7SWoQ/3ZgX9yPrPCr7/Xmfs+3rONj7+2zYmrxlFvVrZ+uWKixfr9Htjx0L37jqlngjExen0gkePwvbt+mWG99yjs0ktWQL16gX61zTG+FlxgW5fEh0gO15bCMB5rKTz5clsdR34e6up9L3+cfoCtGgBSz6Hs86CzEyd83XECG2B33qrBnqTJrlzobZpoz9nzw7I72OMCTwL9Kr2zTdsiYqlc9IiDjZsTcODKTx/3my2N+vFbR89rvO6Xn01DB6cOzdr48Y68bVPs2YBKd0YU71ZoFeGI0fgmWfw3Dyeo01bUveDf/J99ACOfracns/dzKEmg+nPlxy96bew9nOGbfgzHD6s/dkzZ+rk1sYYU0YW6JXhz3+GqVP59k8L+OToJTwiT9KOKCLIYQsd6bl/KQCR110G53XTb1H41a+0b9zC3BhTThbo/vLjjzBsGFx/PZ7npvEDZ9PzyEp6spKl0aOIjnG0OL6N/4v9lEePPky7tR/C+efrV9/ceGOgqzfGhAAb5eIvkybBdB1WeLxGbfo2+J4VN71IncQ18PHH+r1pPiJw/Hjud6sZY0wpFTfKpUZVFxMycnLY8fBLbGp4Lkn//Eq/PXjMGL79v0+4xvM+N/2+PXVe+Av873/5wxx0TLaFuTHGz6zLpTxE8Fw5nDYLF3CMWtT45WCQE0zZ/iuenjOIFq1h7p2BLtIYE26shV4eM2dSY+ECHuRppt+8hiypxybO5tVNA7n/fli+3I5tGmOqnrXQS8HjgdRUPdeH9HSOTPwtq+nPvvG/5c9v1GBmp/Xs3Qubn3Q0bhzoao0x4coCvRReew3uvBO++goaTnuJs3/O4F+DX+HlV/UDzs2/bxvgCo0xxrpcSmXWLJ2rasIdOdT/12t81eBSnlnYjcjIQFdmjDG5rIVegt27oeHnn7Cw6Sw+XX8urdlB9mPP2SAVY0y1Y4FelD17YOZMDr6/gY/5J+yDy5jN4YYxtL97eKCrM8aYU1igF2bPHhg4EH76iVYRDZnVZCI3JtwLU6ZQ9+KLsb4WY0x1ZIFe0JYtcNVVyK5dPHzBcp764gKmPw50BN59N9DVGWNMkSzQ81qxAq64gmPHYUztf/PRVxcwfTr85jeBLswYY0pmge5z6BCMGcPPtZvQff9nxHTvyFfT4NxzA12YMcaUTqmGLTrnhjrnfnDObXbOTS7k/rbOuSXOubXOuW+dc8P8X2ol+93vkO3bue7w2zTq2ZGlSy3MjTHBpcRAd85FAC8ClwNdgTHOua4FVnsEmCMivYDRQDHfTlwNJSXByy+zOPZulh4/n9mzbe4sY0zwKU0LvS+wWUSSROQ4MBsYUWAdARp6rzcCdvmvxCrw5puIc/xm6/1cf71+jacxxgSb0gR6K2BHntsp3mV5TQXGOudSgAVA8BxG9Hhg5kx2d7uETVltGD8+0AUZY0z5+OvU/zHAmyLSGhgGvO2cO2Xbzrk7nHMJzrmEtLQ0Pz11BS1cCNu384ZnPB066PBzY4wJRqUJ9J1Amzy3W3uX5XUrMAdARFYAUUDzghsSkRkiEi8i8dHR0eWr2F+OHdOvjLviCrKbncYfN17N+PFQw2a3McYEqdLE1yqgs3Oug3OuFnrQc36BdbYDQwCcc13QQK8mTfAirF4Nn34KEydy93kJ1KwfxZ32pRTGmCBWYqCLSDYwEVgEbEJHs2x0zj3hnPNNanI/cLtzbj3wLjBOAvVlpaW1ejUAm0ZM5pV/t2HSJGjWLMA1GWNMBZTqxCIRWYAe7My77NE81xOB/v4trZKtXg0xMUyf25J69eC++wJdkDHGVEz49hivWQO9e7NkqWPwYGjaNNAFGWNMxYRnoB85AomJZJ3dhx9+sJEtxpjQEJ6Bvn495OSwPqIPAIMGBbgeY4zxg/AM9DVrAFiY1od69aBXrwDXY4wxfhBesy3u2we33w6ffQbR0cxf05rzz7fvqzDGhIbwaaF7PHDzzfDxxzB6NLun/YvvNjjrPzfGhIzwaaFPnw6ffAIvvIDcNZHxl0O9eprxxhgTCsIn0F9/HS64AO66i3fegUWL4IUXoE2bkh9qjDHBIDy6XNLTYcMGuPxycI5p06BHD5gwIdCFGWOM/4RHoC9frj8HDSI5GRISYOxYiIgIbFnGGONP4RHoS5dCnTpwzjnMnauLrrsuoBUZY4zfhUegL1sG550HtWrx3nsQHw8dOgS6KGOM8a/QD/T9++Hbb2HQIHbsgFWrrHVujAlNoR/oq1aBCPTvz7JluujyywNbkjHGVIbQD/RNm/Rnt2588QU0agSxsYEtyRhjKkN4BHqTJnDaaSxfDuefb6NbjDGhKTwCvUsXMvY5EhP13CJjjAlFYRPoX32lNwcMCGw5xhhTWUI70NPTIS0NunZl+XKoVQvOOSfQRRljTOUI7UD3HRDt0oWVK6F3b4iKCmxJxhhTWcIi0D1ndWHdOg10Y4wJVaEf6HXrkpTdlkOH7JuJjDGhLbQD/fvv4ayzWLtef82ePQNcjzHGVKLQDvSUFGjblrVrdex5t26BLsgYYypPqQLdOTfUOfeDc26zc25yIfc/55xb57386JzL9H+p5ZCaCjExrFsHXbvaAVFjTGgr8RuLnHMRwIvAJUAKsMo5N19EEn3riMi9edb/DRD43ursbB22GBPD2vlw6aWBLsgYYypXaVrofYHNIpIkIseB2cCIYtYfA7zrj+IqJD0dRDhQ93T27LEDosaY0FeaQG8F7MhzO8W77BTOuXZAB2BxEfff4ZxLcM4lpKWllbXWsklNBWBpYgxgp/wbY0Kfvw+KjgbmikhOYXeKyAwRiReR+OjoaD8/dQHeQH/1wxiGDtUvtTDGmFBWYh86sBNok+d2a++ywowG7qpoUX7hDfSfDsUw5/8CXIsxxlSB0rTQVwGdnXMdnHO10NCeX3Al59zZQBNghX9LLCdvoJ95QYz1nxtjwkKJgS4i2cBEYBGwCZgjIhudc08454bnWXU0MFtEpHJKLaM9ezhKFKd1ahDoSowxpkqUpssFEVkALCiw7NECt6f6r6yKkz2p7CGGFi1doEsxxpgqEbJnip7YmUoqMZx+eqArMcaYqhGygZ6zSwO9RYtAV2KMMVUjZAO9Rpq10I0x4SU0Az0nh8jMNGuhG2PCSmgGekYGNcRjLXRjTFgJzUD3jkE/UDuG+vUDXIsxxlSR0Az0LVsAyI625rkxJnyEZqBPm0Z6rRbsbdc30JUYY0yVKdWJRUFl2TJYtoxXT5tGs1b2jRbGmPARei30v/wFYmKYfuQOOyBqjAkroRfoCQlkD72SvYfq2JBFY0xYCa1A//lnSE3lYPOOANZCN8aEldAK9K1bAUir3wHAWujGmLASWoGelATAtpraQm9V6BflGWNMaAqtQE9OBmDjz9pC79gxkMUYY0zVCq1AT0qCevXYkBpNixZQt26gCzLGmKoTWoGenAwdOpCU7Kx1bowJO6EV6ElJ0LEjW7ZYd4sxJvyETqCLQHIy2e06kpICnToFuiBjjKlaoRPoaWnw889kNOiAiLXQjTHhJ3QC3TvCZUekJrkFujEm3IROoHtPKvrpRHvAAt0YE35CJ9D37gUgMSOGOnXstH9jTPgpVaA754Y6535wzm12zk0uYp3rnXOJzrmNzrl3/FtmKezdC86xcXdTOnYE56q8AmOMCagS50N3zkUALwKXACnAKufcfBFJzLNOZ+AhoL+I7HfOnVZZBRcpLQ2aNydpWwQdOlT5sxtjTMCVpoXeF9gsIkkichyYDYwosM7twIsish9ARPb6t8xSSEuD6Gj27LFJuYwx4ak0gd4K2JHndop3WV5nAmc65750zq10zg0tbEPOuTuccwnOuYS0tLTyVVyUtDQkOpq0NDit6j8fGGNMwPnroGhNoDMwGBgD/N0517jgSiIyQ0TiRSQ+OjraT0/tlZbG8YbReDwQE+PfTRtjTDAoTaDvBNrkud3auyyvFGC+iJwQkWTgRzTgq05aGj/X1TcJa6EbY8JRaQJ9FdDZOdfBOVcLGA3ML7DOh2jrHOdcc7QLJsmPdRYvOxsyMjhQSwPdWujGmHBUYqCLSDYwEVgEbALmiMhG59wTzrnh3tUWARnOuURgCfCAiGRUVtGnyNCnyqipTXNroRtjwlGJwxYBRGQBsKDAskfzXBfgPu+l6nkPsO71WAvdGBO+QuNMUW+g7zoRTc2a0KRJgOsxxpgACKlA334kmuhoqBEav5UxxpRJaESfN9CTs6Ktu8UYE7ZCKtC3ZDazA6LGmLAVGoG+dy80a8auvTWthW6MCVuhEeje0/737rUhi8aY8BUygZ7TNJojR2zIojEmfIVMoB9tYGPQjTHhLWQCPSvK5nExxoS34A/0nBzIyCAz0gLdGBPegj/Q9+0Dj4c075ck2ZdbGGPCVfAHuncM+u7saGrUsBa6MSZ8hUygbz8SzemnQ0REgOsxxpgACZlATzoUbd0txpiwFjKB/uP+aFq2DHAtxhgTQCET6Il7m1ugG2PCWvAH+t69SJMm7E6PtC4XY0xYC/5AT0sju4mOQbcWujEmnIVEoB+tb4FujDEhEeiHoizQjTEmJAJ9f00NdOtDN8aEs+AOdI8H0tNJc6cREQHR0YEuyBhjAie4A33/fsjJYdcJO0vUGGOCO9DznPZv3S3GmHBXqkB3zg11zv3gnNvsnJtcyP3jnHNpzrl13stt/i+1EHlO+7cDosaYcFezpBWccxHAi8AlQAqwyjk3X0QSC6z6LxGZWAk1Fi1PoHewWRaNMWGuNC30vsBmEUkSkePAbGBE5ZZVSnv3ApCcFU2TJgGuxRhjAqw0gd4K2JHndo6bw+kAABJVSURBVIp3WUHXOue+dc7Ndc61KWxDzrk7nHMJzrmENG/rukJ270Zq1GDbsRgaN6745owxJpj566Dox0B7EekBfAbMLGwlEZkhIvEiEh/tjzGGO3fiiY4hh5oW6MaYsFeaQN8J5G1xt/YuO0lEMkTkmPfma0Af/5RXgl27ON5cj4Zal4sxJtyVJtBXAZ2dcx2cc7WA0cD8vCs45/IOGhwObPJficXYtYsjTTTQrYVujAl3JY5yEZFs59xEYBEQAbwhIhudc08ACSIyH7jbOTccyAb2AeMqseZcu3aRFd8PsEA3xpgSAx1ARBYACwosezTP9YeAh/xbWgmOHYO0NDLrWZeLMcZAMJ8pumcPABm1dcCNtdCNMeEueAN91y4AUiOsD90YYyAEAn23a0lUFERFBbgeY4wJsOAN9J06cnJHTktrnRtjDMEc6Lt2QWQkKUeaWaAbYwzBHugtW7L/QA0b4WKMMYRAoGdm2gFRY4yBYA70nTu1hb7fAt0YYyCYA333bmjRgsxMO6nIGGMgWAP9xAk4cABpHm1dLsYY4xWcgZ6eDsCxhtHk5FigG2MMBHmgZ0U1B6zLxRhjIMgD/WAtDXRroRtjTJAH+r4I/dYjC3RjjAnyQM9w1kI3xhif4Ax07xdM781pBlgfujHGQLAGeno6NGrEvkORgLXQjTEGgjnQo3UMOkCjRoEtxxhjqoPgDfTmzcnMhAYNoGapvkjPGGNCW3AGeloaNG9u87gYY0wewRnoebpcLNCNMUYFX2eFSG6XS5KNcDHB7cSJE6SkpHD06NFAl2KqmaioKFq3bk1kZGSpHxN8gX74MBw9erLLpX37QBdkTPmlpKTQoEED2rdvj3Mu0OWYakJEyMjIICUlhQ4dOpT6caXqcnHODXXO/eCc2+ycm1zMetc658Q5F1/qCsrKe1KR76CodbmYYHb06FGaNWtmYW7ycc7RrFmzMn9yKzHQnXMRwIvA5UBXYIxzrmsh6zUAJgFfl6mCsvKeVOTrQ7cuFxPsLMxNYcrzuihNC70vsFlEkkTkODAbGFHIek8CTwOV2xnobaHnNGnOwYPWQjfGGJ/SBHorYEee2yneZSc553oDbUTk38VtyDl3h3MuwTmXkOZraZeVN9AP1bZ5XIwxJq8KD1t0ztUAngXuL2ldEZkhIvEiEh8dHV2+J/QGemakPt66XIypmMzMTF566aUyP27YsGFk+k7XNtVCaUa57ATa5Lnd2rvMpwHQDVjq7fM5HZjvnBsuIgn+KvSkPn3gwQfJyNbz/a2FbkLFPffAunX+3WbPnjBtWvHr+AL9zjvvzLc8OzubmsWchr1gwQJ/lFhpSqo/FJWmhb4K6Oyc6+CcqwWMBub77hSRAyLSXETai0h7YCVQOWEOMGAAPP00mQf0gIEFujEVM3nyZLZs2ULPnj0555xzGDBgAMOHD6drVx37cPXVV9OnTx9iY2OZMWPGyce1b9+e9PR0tm7dSpcuXbj99tuJjY3l0ksv5ciRI0U+39///nfOOecc4uLiuPbaazl8+DAAqampXHPNNcTFxREXF8dXX30FwFtvvUWPHj2Ii4vjpptuAmDcuHHMnTv35Dbr168PwNKlS0td/8KFC+nduzdxcXEMGTIEj8dD586d8XUHezwezjjjDMrdPRwIIlLiBRgG/AhsAaZ4lz2BBnfBdZcC8SVts0+fPlIRc+eKgMj69RXajDEBlZiYGOgSJDk5WWJjY0VEZMmSJVK3bl1JSko6eX9GRoaIiBw+fFhiY2MlPT1dRETatWsnaWlpkpycLBEREbJ27VoRERk1apS8/fbbRT6f7/EiIlOmTJHp06eLiMj1118vzz33nIiIZGdnS2ZmpmzYsEE6d+4saWlp+Wq5+eab5b333ju5nXr16pWp/r1790rr1q1PrudbZ+rUqSdrWLRokYwcObK0u7FSFPb6ABKkiFwt1ecREVkALCiw7NEi1h1crneWMtq/X39aC90Y/+rbt2++k1mmT5/OvHnzANixYwc//fQTzZo1y/eYDh060LNnTwD69OnD1q1bi9z+hg0beOSRR8jMzCQrK4vLLrsMgMWLF/PWW28BEBERQaNGjXjrrbcYNWoUzZvrIIimTZv6pf60tDQGDhx4cj3fdm+55RZGjBjBPffcwxtvvMH48eNLfL7qJGg7mHzHYizQjfGvevXqnby+dOlS/vvf/7JixQrq1q3L4MGDCz3ZpXbt2ievR0REFNvlMm7cOD788EPi4uJ48803Wbp0aZlrrFmzJh6PB9CukePHj1eofp82bdoQExPD4sWL+eabb5g1a1aZawuk4JycCw30GjV0+lxjTPk1aNCAQ4cOFXrfgQMHaNKkCXXr1uX7779n5cqVFX6+Q4cO0aJFC06cOJEvMIcMGcLLL78MQE5ODgcOHOCiiy7ivffeIyMjA4B9+/YB2n+/evVqAObPn8+JEyfKVH+/fv34/PPPSU5OzrddgNtuu42xY8cyatQoIiIiKvz7VqWgDXTf1Ll2kp0xFdOsWTP69+9Pt27deOCBB/LdN3ToULKzs+nSpQuTJ0+mX79+FX6+J598knPPPZf+/ftz9tlnn1z+/PPPs2TJErp3706fPn1ITEwkNjaWKVOmMGjQIOLi4rjvvvsAuP3221m2bBlxcXGsWLEiX6u8NPVHR0czY8YMRo4cSVxcHDfccMPJxwwfPpysrKyg624BcNrHXvXi4+MlIaH8A2FuvBFWroQtW/xYlDFVbNOmTXTp0iXQZZg8EhISuPfee1m+fHmgSyn09eGcWy0ihc6XFdR96HZSkTHGn5566ilefvnloOs79wn6LhdjTPV011130bNnz3yXf/zjH4Euq1iTJ09m27ZtXHDBBYEupVyCuoXesmWgqzDGFOXFF18MdAlhJ2hb6NblYowx+QVloB8/DqmpEBMT6EqMMab6CMpA37YNPB7o3DnQlRhjTPURlIG+ebP+POOMwNZhjDHViQW6MaZMfDMb7tq1i+uuu67QdQYPHkxJ55lMmzbt5EyLYPOr+0NQjnLZvBnq14fTTgt0Jcb4UaAmRC+nli1b5pvCtqymTZvG2LFjqVu3LlD951cvSnWadz1oW+hnnGGn/RvjD5MnT843xHDq1Kn84Q9/YMiQIfTu3Zvu3bvz0UcfnfK4rVu30q1bNwCOHDnC6NGj6dKlC9dcc02+ybkmTJhAfHw8sbGxPPbYY4DOgLhr1y4uvPBCLrzwQiB3fnWAZ599lm7dutGtWzemed+QbN71UihqXt3KvlRkPvQzzxS57rpyP9yYaqM6zIe+Zs0aGThw4MnbXbp0ke3bt8uBAwdERCQtLU06deokHo9HRHLnHs87j/pf//pXGT9+vIiIrF+/XiIiImTVqlUikjvXeHZ2tgwaNEjWe7/EwDefuo/vdkJCgnTr1k2ysrLk0KFD0rVrV1mzZk1Yzrte1vnQg66Fnp0NycnWf26Mv/Tq1Yu9e/eya9cu1q9fT5MmTTj99NN5+OGH6dGjBxdffDE7d+4kNTW1yG18/vnnjB07FoAePXrQo0ePk/fNmTOH3r1706tXLzZu3EhiYmKx9XzxxRdcc8011KtXj/r16zNy5MiT86qUdd71AQMG0L17d2bNmsXGjRsBnXd9woQJQO6864sXL/bLvOtxcXH069fv5LzrK1euLHLedd/c7/6cd716dPyUwY4dcOKEBbox/jRq1Cjmzp3Lnj17uOGGG5g1axZpaWmsXr2ayMhI2rdvX+w84kVJTk7mmWeeYdWqVTRp0oRx48aVazs+Nu968YKuhW4jXIzxvxtuuIHZs2czd+5cRo0axYEDBzjttNOIjIxkyZIlbNu2rdjHDxw4kHfeeQfQlvG3334LwMGDB6lXrx6NGjUiNTWVTz/99ORjipqHfcCAAXz44YccPnyYn3/+mXnz5jFgwIAy/07hOO+6BboxhtjYWA4dOkSrVq1o0aIFN954IwkJCXTv3p233nor37zlhZkwYQJZWVl06dKFRx99lD59+gAQFxdHr169OPvss/nFL35B//79Tz7mjjvuYOjQoScPivr07t2bcePG0bdvX84991xuu+02evXqVebfKRznXQ+6+dA/+gjefBPef1+/sciYYGbzoYev0sy7HvLzoY8YoRdjjAlWlTXvurVxjTFBzeZdzxV0LXRjQo2I4OwsuXIL1XnXy9Mdbi10YwIoKiqKjIyMcv3zmtAlImRkZBAVFVWmx5Wqhe6cGwo8D0QAr4nIUwXu/zVwF5ADZAF3iEjxZw8YY2jdujUpKSn+Oe3bhJSoqChat25dpseUGOjOuQjgReASIAVY5ZybXyCw3xGRV7zrDweeBYaWqRJjwlBkZGS+sw2NqYjSdLn0BTaLSJKIHAdmA/nGmYjIwTw36wH2+dEYY6pYabpcWgE78txOAc4tuJJz7i7gPqAWcFFhG3LO3QHcAdC2bduy1mqMMaYYfjsoKiIvikgn4HfAI0WsM0NE4kUkPjo62l9PbYwxhtK10HcCbfLcbu1dVpTZwMslbXT16tXpzrniJ4goWnMgvZyPrWzVtTarq2ysrrKrrrWFWl3tirqjNIG+CujsnOuABvlo4Bd5V3DOdRaRn7w3rwB+ogQiUu4munMuoahTXwOtutZmdZWN1VV21bW2cKqrxEAXkWzn3ERgETps8Q0R2eicewKdaH0+MNE5dzFwAtgP3OzPIo0xxpSsVOPQRWQBsKDAskfzXJ/k57qMMcaUUbCeKTqj5FUCprrWZnWVjdVVdtW1trCpK2DT5xpjjPGvYG2hG2OMKcAC3RhjQkTQBbpzbqhz7gfn3Gbn3OQA1tHGObfEOZfonNvonJvkXT7VObfTObfOexkWgNq2Oue+8z5/gndZU+fcZ865n7w/m1RxTWfl2SfrnHMHnXP3BGp/OefecM7tdc5tyLOs0H3k1HTva+5b51zvKq7rL865773PPc8519i7vL1z7kieffdKFddV5N/OOfeQd3/94Jy7rLLqKqa2f+Wpa6tzbp13eZXss2LyoXJfYyISNBd02OQWoCM6xcB6oGuAamkB9PZebwD8CHQFpgK/DfB+2go0L7Dsz8Bk7/XJwNMB/jvuQU+QCMj+AgYCvYENJe0jYBjwKeCAfsDXVVzXpUBN7/Wn89TVPu96Adhfhf7tvP8H64HaQAfv/2xEVdZW4P6/Ao9W5T4rJh8q9TUWbC30EicKqyoisltE1nivHwI2ofPeVFcjgJne6zOBqwNYyxBgi4iU90zhChORz4F9BRYXtY9GAG+JWgk0ds61qKq6ROQ/IpLtvbkSPVu7ShWxv4oyApgtIsdEJBnYjP7vVnltzjkHXA+8W1nPX0RNReVDpb7Ggi3QC5soLOAh6pxrD/QCvvYumuj92PRGVXdteAnwH+fcaqcTogHEiMhu7/U9QEwA6vIZTf5/sEDvL5+i9lF1et3dgrbkfDo459Y655Y55wYEoJ7C/nbVaX8NAFIl90x2qOJ9ViAfKvU1FmyBXu045+oD7wP3iE4j/DLQCegJ7EY/7lW1C0SkN3A5cJdzbmDeO0U/4wVkvKpzrhYwHHjPu6g67K9TBHIfFcU5NwXIBnzfLLwbaCsivdCZTt9xzjWswpKq5d+ugDHkbzxU6T4rJB9OqozXWLAFelknCqtUzrlI9I81S0Q+ABCRVBHJEREP8Hcq8aNmUURkp/fnXmCet4ZU30c478+9VV2X1+XAGhFJ9dYY8P2VR1H7KOCvO+fcOOBK4EZvEODt0sjwXl+N9lWfWVU1FfO3C/j+AnDO1QRGAv/yLavKfVZYPlDJr7FgC/STE4V5W3qjgfmBKMTbN/c6sElEns2zPG+/1zXAhoKPreS66jnnGviuowfUNqD7yTfHzs3AR1VZVx75WkyB3l8FFLWP5gO/9I5E6AccyPOxudI5/QrIB4HhInI4z/Jop98ohnOuI9AZSKrCuor6280HRjvnajud1K8z8E1V1ZXHxcD3IpLiW1BV+6yofKCyX2OVfbTX3xf0aPCP6DvrlADWcQH6celbYJ33Mgx4G/jOu3w+0KKK6+qIjjBYD2z07SOgGfA/dCbM/wJNA7DP6gEZQKM8ywKyv9A3ld3ohHIpwK1F7SN05MGL3tfcd0B8Fde1Ge1f9b3OXvGue633b7wOWANcVcV1Ffm3A6Z499cPwOVV/bf0Ln8T+HWBdatknxWTD5X6GrNT/40xJkQEW5eLMcaYIligG2NMiLBAN8aYEGGBbowxIcIC3RhjQoQFujHGhAgLdGOMCRH/DxRzKJ0hFbdkAAAAAElFTkSuQmCC\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWoAAAD4CAYAAADFAawfAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3deXxU5b3H8c+ThSwsIYQACQEJgmwugAHxItbWthcRxSporRtqS7W0StX24qub66ut9XqtV4WrFeu1KlIt6rVSWxXFFWWNrAIaBBIJJECALGR57h+/GRIwgQSTmZPk+3695pXJLOf85szM9zznOc8547z3iIhIcMVEuwARETkyBbWISMApqEVEAk5BLSIScApqEZGAi2uJiXbv3t3369evJSYtItImLV26dKf3Pr2++1okqPv168eSJUtaYtIiIm2Sc25zQ/ep60NEJOAU1CIiAaegFhEJuBbpoxaRyKmsrGTr1q2Ul5dHuxRphMTERLKysoiPj2/0cxTUIq3c1q1b6dy5M/369cM5F+1y5Ai89xQVFbF161ays7Mb/Tx1fYi0cuXl5aSlpSmkWwHnHGlpaU3e+lFQi7QBCunW41jeq0AF9Z13wquvRrsKEZFgCVRQ33OPglpE5HCBCurkZCgri3YVItIUu3fv5uGHH27y8yZMmMDu3bub/LypU6fy3HPPNfl5rVmggjopCUpLo12FiDRFQ0FdVVV1xOe98sordO3ataXKalMCNTwvOVlBLfJVzJgBK1Y07zSHD4f772/4/pkzZ7Jp0yaGDx9OfHw8iYmJpKamsm7dOj755BMuuOACtmzZQnl5OTfeeCPTpk0Das8JtG/fPs455xzOOOMM3nvvPXr37s2LL75IUlLSUWt7/fXXueWWW6iqqmLUqFHMmjWLhIQEZs6cyUsvvURcXBzf/va3uffee/nrX//K7bffTmxsLCkpKSxatKi5FlGLU1CLyFfyu9/9jlWrVrFixQrefPNNzj33XFatWnVwnPCcOXPo1q0bZWVljBo1iosuuoi0tLRDprFhwwaeeeYZHn30US6++GKef/55Lr/88iPOt7y8nKlTp/L6669zwgkncOWVVzJr1iyuuOIK5s+fz7p163DOHexeueOOO3j11Vfp3bv3MXW5RFPgglp91CLH7kgt30gZPXr0IQdzPPDAA8yfPx+ALVu2sGHDhi8FdXZ2NsOHDwfg1FNPJS8v76jzWb9+PdnZ2ZxwwgkAXHXVVTz00EP8+Mc/JjExkWuvvZaJEycyceJEAMaOHcvUqVO5+OKLufDCC5vjpUaM+qhFpFl17Njx4PU333yT1157jffff5+VK1cyYsSIeg/2SEhIOHg9Njb2qP3bRxIXF8eHH37I5MmTefnllxk/fjwAs2fP5q677mLLli2ceuqpFBUVHfM8Ii1wLeqCgmhXISJN0blzZ/bu3VvvfXv27CE1NZXk5GTWrVvHBx980GzzHTRoEHl5eWzcuJEBAwbw5JNP8rWvfY19+/ZRWlrKhAkTGDt2LP379wdg06ZNnHbaaZx22mksWLCALVu2fKllH1SBC2q1qEVal7S0NMaOHcuJJ55IUlISPXv2PHjf+PHjmT17NkOGDGHQoEGMGTOm2eabmJjI448/zpQpUw7uTLzuuusoLi5m0qRJlJeX473nvvvuA+BnP/sZGzZswHvP2WefzSmnnNJstbQ0571v9onm5OT4Y/mFlx/8AF55BbZta/aSRNqstWvXMmTIkGiXIU1Q33vmnFvqvc+p7/HqoxYRCTh1fYhIIE2fPp133333kNtuvPFGrr766ihVFD2BC+oDB6C6GmJjo12NiETTQw89FO0SAiNQXR/JyfZXY6lFRGoFKqjDR4yq+0NEpFajg9o5F+ucW+6ce7mligm3qBXUIiK1mtKivhFY21KFgLo+RETq06igds5lAecCf2rJYtSiFmn7OnXqBEB+fj6TJ0+u9zFnnXUWRzsW4/7776e0Tlgc6/mtGxKk8143tkV9P/BzoKYFa1EftUg7kpmZ+ZWC8PCgbsvntz7q8Dzn3ESg0Hu/1Dl31hEeNw2YBtC3b99jKkYtapGvKAonpJ45cyZ9+vRh+vTpANx2223ExcWxcOFCdu3aRWVlJXfddReTJk065Hl5eXlMnDiRVatWUVZWxtVXX83KlSsZPHgwZXX6P6+//no++ugjysrKmDx5MrfffjsPPPAA+fn5fP3rX6d79+4sXLjw4Pmtu3fvzn333cecOXMA+P73v8+MGTPIy8trtee9bkyLeixwvnMuD5gLfMM595fDH+S9f8R7n+O9z0lPTz+mYtRHLdL6XHLJJcybN+/g//PmzeOqq65i/vz5LFu2jIULF3LzzTdzpNNVzJo1i+TkZNauXcvtt9/O0qVLD9539913s2TJEnJzc3nrrbfIzc3lhhtuIDMzk4ULF7Jw4cJDprV06VIef/xxFi9ezAcffMCjjz7K8uXLATvv9fTp01m9ejVdu3bl+eefP+rrC5/3+tlnn+Xjjz+mqqqKWbNmUVRUxPz581m9ejW5ubn88pe/BGrPe71y5UpeeumlJi3Lhhy1Re29vxW4FSDUor7Fe3/kM3ofI7WoRb6iKJyQesSIERQWFpKfn8+OHTtITU2lV69e/PSnP2XRokXExMSwbds2tm/fTq9eveqdxqJFi7jhhhsAOPnkkzn55JMP3jdv3jweeeQRqqqqKCgoYM2aNYfcf7h33nmH73znOwdPt3rhhRfy9ttvc/7557fa815rHLWIfGVTpkzhueee49lnn+WSSy7hqaeeYseOHSxdupQVK1bQs2fPes9DfTSfffYZ9957L6+//jq5ubmce+65xzSdsNZ63usmBbX3/k3v/cSvPNcGqOtDpHW65JJLmDt3Ls899xxTpkxhz5499OjRg/j4eBYuXMjmzZuP+PwzzzyTp59+GoBVq1aRm5sLQElJCR07diQlJYXt27ezYMGCg89p6DzY48aN44UXXqC0tJT9+/czf/58xo0bd8yvre55r4FDznu9Z88eJkyYwH/913+xcuVKoPa813fccQfp6els2bLlmOcdFrhzfYBa1CKtzbBhw9i7dy+9e/cmIyODyy67jPPOO4+TTjqJnJwcBg8efMTnX3/99Vx99dUMGTKEIUOGcOqppwJwyimnMGLECAYPHkyfPn0YO3bswedMmzaN8ePHH+yrDhs5ciRTp05l9OjRgO1MHDFiRKO6OeoThPNeB+p81N5DTAz8+tdw++3NXpZIm6TzUbc+rfp81M7pnNQiIocLVNcH6JfIRSSyWsN5rwMZ1GpRizSN9x7nXLTLaJUifd7rY+luDlTXByioRZoqMTGRoqKiYwoAiSzvPUVFRSQmJjbpeYFrUauPWqRpsrKy2Lp1Kzt27Ih2KdIIiYmJZGVlNek5gQtq9VGLNE18fDzZ2dnRLkNakLo+REQCTkEtIhJwgQvqpCR1fYiI1BW4oFaLWkTkUApqEZGAU1CLiARc4II63EetsfsiIiZwQR0+1elXODe4iEibEtig3r8/unWIiARF4IK6Uyf7q6AWETHBCur0dMb83y8A2LcvyrWIiAREsIK6upqkGkvoen4KTUSkXQpWUCcnk1htY/PUohYRMYEL6g4KahGRQwQvqKsU1CIidQUuqOMPKKhFROoKXFDHKahFRA4RuKCOqVBQi4jUFbigdvv307GjhueJiIQFLqgpLaVTJ7WoRUTCFNQiIgEXyKDu3FlBLSISFrygLiujc8caBbWISEjwghrollyuoBYRCQlmUCeWKqhFREICGdSpCaUaniciEhLYoFaLWkTEBDKoU+IV1CIiYYEM6i5xpVRWwoEDUa5HRCQAAhvUoLHUIiIQ0KDuHKugFhEJO2pQO+cSnXMfOudWOudWO+dub7FqQkHdKUZBLSISFteIx1QA3/De73POxQPvOOcWeO8/aPZqQkGd7CyoNURPRKQRQe2990C4bRsfuvgWqSYc1F4tahGRsEb1UTvnYp1zK4BC4F/e+8X1PGaac26Jc27Jjh07jq2aUFAnKahFRA5qVFB776u998OBLGC0c+7Eeh7ziPc+x3ufk56efmzVJCSAcyTWKKhFRMKaNOrDe78bWAiMb5FqnIPkZBKqFdQiImGNGfWR7pzrGrqeBHwLWNdiFSUn06FKQS0iEtaYUR8ZwBPOuVgs2Od5719usYqSk4mrVFCLiIQ1ZtRHLjAiArWY5GRiykpJTtbwPBERCNqRiXDI7yYqqEVEAhzUnTsrqEVEIMBBnZICJSXRLkZEJPoCG9RduiioRUQg4EG9Z0+0ixERib5AB7Va1CIiAQ5q9VGLiJjABnW4Re1b5jx9IiKtRjCDurKSrh0rqaqCsrJoFyQiEl3BDGogLckOI1f3h4i0d8EL6i5dAOgWZwmtoBaR9i54Qd2tm/2hGFBQi4gEL6hTUwHo6ncBGkstIhK8oA61qLtUqUUtIgJBDOpQi7pTpbWoFdQi0t4FNqiTK9T1ISICQQzqTp0gLo7EUnV9iIhAEIPaOUhNJbZkF4mJCmoRkeAFNdgOxeJinZhJRISgBnVqKuzaRUqK+qhFRIIZ1GpRi4gcFMygDrWoFdQiIkEN6m7dDnZ9KKhFpL0LZlCnpsLu3aR0rlEftYi0e8ENau/pkbBHLWoRafeCGdSh8330jC/Wr7yISLsXzKAOHUaeHreL6mooLY1yPSIiURTMoA6fk9rpxEwiIsEM6lCLOvzjAcXF0SxGRCS6ghnUoRZ191hrUW/fHs1iRESiK5hBHf6VlxprSiuoRaQ9C2ZQJyRAUhKdq9WiFhEJZlADpKWRuG8n8fEKahFp34Ib1BkZuIICevRQUItI+xbcoM7MhIICevZUUItI+xbcoM7IgPx8BbWItHvBDerMTNi5k8zuBxTUItKuBTeoMzIAOL7TFxQW6nwfItJ+HTWonXN9nHMLnXNrnHOrnXM3RqIwMjMB6Befz4EDsHt3ROYqIhI4jWlRVwE3e++HAmOA6c65oS1bFgeDOtMVAOqnFpH266hB7b0v8N4vC13fC6wFerd0YeGuj57V+YCCWkTaryb1UTvn+gEjgMX13DfNObfEObdkx44dX72y9HSIjaVbuYJaRNq3Rge1c64T8Dwww3v/pROPeu8f8d7neO9z0tPTm6GyGOjVi8771PUhIu1bo4LaORePhfRT3vu/tWxJdWRmklicT0wMFBZGbK4iIoHSmFEfDngMWOu9v6/lS6ojIwP3RQHp6WpRi0j71ZgW9VjgCuAbzrkVocuEFq7LZGZCfj69ekFBQUTmKCISOHFHe4D3/h3ARaCWL8vIgJ07OS7nAFvzO0SlBBGRaAvukYlwcCz14K5fsG1blGsREYmSVhHUAzvmU1gIlZVRrkdEJAqCHdShg16O61CA9/DFF1GuR0QkCoId1KEWdYa3g17U/SEi7VGwgzp0dGL3KhvykZ8f5XpERKIg2EEdOjoxZZ9a1CLSfgU7qAEyMkgszic+Xi1qEWmfgh/UmZm4LwrIzFSLWkTap1YR1OTnK6hFpN0KflCHj07MOKCuDxFpl4If1KEheoNSdHSiiLRPwQ/q8I/cJuWzdy/s3RvlekREIiz4QR1qUfeNt7HUalWLSHsT/KAOH0Yebx3Ua9dGsxgRkcgLflCHjk7sHVNATAysWBHtgkREIiv4QR0bCz17El+4jcGDYfnyaBckIhJZwQ9qgOxs2LSJ4cPVohaR9qd1BPWwYbB6NSOGe7ZsgaKiaBckIhI5rSOohw6F4mJG97OfIlerWkTak9YR1MOGAXBK3GpAQS0i7UvrCOqhQwFI2bqarCztUBSR9qV1BHVGBnTtCmvWMHQofPJJtAsSEYmc1hHUzh3codivH3z2WbQLEhGJnNYR1GDdH6tXk93Ps3Mn7NsX7YJERCKj9QT1sGFQXMzgrvZT5Hl50S1HRCRSWk9Qn3kmAKe9fS+g7g8RaT9aT1CPGAE//CG9nr2fHD5Si1pE2o3WE9QAv/899OjBHTG3q0UtIu1G6wrqlBTc2WczPCZXQS0i7UbrCmqAIUPIqNrC9k0a9iEi7UOrDGqADp+ui3IhIiKR0WqDus/+tezeHeVaREQioPUF9YAB1MTGMYS1zJsHNTXRLkhEpGW1vqCOj8f3H8Dozmv54Q9h2rRoFyQi0rJaX1ADsScO4ezMtUyeDC+8AN5HuyIRkZbTKoOaIUNwGzfyjTMOUFQE27ZFuyARkZbTaoOa6mrGdN8I6IcERKRta51BfdJJAAwuX4FzCmoRaduOGtTOuTnOuULn3KpIFNQow4ZBUhJJqz5iwAAFtYi0bY1pUf8ZGN/CdTRNXByMHAkffsjw4QpqEWnbjhrU3vtFQHEEammaUaNg+XJGnFTFpk1QUhLtgkREWkaz9VE756Y555Y455bs2LGjuSbbsFGjoKyMM1Ltl8mXLWv5WYqIREOzBbX3/hHvfY73Pic9Pb25JtuwUaMAOLXmQzp2hD/9qeVnKSISDa1z1AfAgAHQtSvJqz5i2jSYOxc2b452USIiza/1BrVzMHYsvPgiN00txjm4775oFyUi0vwaMzzvGeB9YJBzbqtz7tqWL6uR7roLiovJuu8mLr8cZs+G9eujXZSISPNqzKiPS733Gd77eO99lvf+sUgU1ijDh8N//Ac88QT/3eNOOiVVc911OveHiLQtrbfrI+xXv4JLL6XTPb9mRdZE3n6ziptugurqaBcmItI8Wn9QJyTAU0/Bgw/SZ/U/eHXETO6/Hy65RC1rEWkbWn9Qg+1YnD4dpk/n7OX/ydNXLOD552HBgmgXJiLy1TnfAs3OnJwcv2TJkmaf7lEdOADDhlGT3JFB+5aR1DGG5cshNjbypYiINIVzbqn3Pqe++9pGizqsQwf4zW+IyV3J/058li8+LmTWw+r/EJHWrW0FNcCll8KQIZz+wPcopCf9b5zI+y8WRrsqEZFjFhftAppdbKztXHzpJcr3VXL2f97L9gtPo+jztaT1Tox2dSIiTdb2ghpgxAgYMYJE4LPssWRPn8DjFz/J1e/+INqViYg0Wdvr+jhM9vXj2dZrJGPf+wOv/ehv+Jm3wv790S5LRKTR2nxQ4xzpf/gPTmAD35x1Ee73v6P01HGwZcuhj6usjE59IiJH0faDGuhw6UX4H0zjg0v/yJUpL1K1fiMlg0dT9cLLMGcOnHEGpKTAO+9Eu1QRkS9pW+OoG6GkBB744Wq+N/c8+vOZ3di/vx1zXlYGH30EfftGt0gRaXfazzjqRujSBX75zDCWPPwRl7h53PCNVcy+eQM/7LuAA3vLqblqau2x5wUFcOWVsH17VGsWkfatbY76aISLr0+j4MAUZswA3oDu3YcQX3Y3D775E7bM/jt9rp8IP/uZDfXr2RP+8Idolywi7VS7a1HXdcMN8OCDMG+eNZrPfvaHbIw9gdLpt/DWNU9YSHfpQs3s/6Fww57aJx44YL9SsHFj9IoXkXajXQd1+FxOU6ZATAx85+J4Uv98PwPYyNcen8rOxN787ZqXidm3l1eHzuCtyx/F79gJN99sl5Ej4dZb4cYbYd066zJ58kn4/PNovzQRaUPa3c7ExqjO387LM9/hnhdP4L2Sk3inyzmMLfkHAJUdOhJ/YD9cey2sXQvvvQdxcZCRARdeCH/8ox1w88Yb9qMGY8daP7eIyBEcaWeigvoI9u61QSBnnFZJ/K5Crr+okHOX3UnOKLiyw7Msy42jU2wZ08at5dYF44gpL7NgfvddSE+HHTtsQtddB0OHQl4e7NljP3Zw3HF2X3W1XTp0sP+9t98TGzTImvwi0i4oqJvJhg1w0klQUQGZmXD++bB7N7z0EpxV8SozTnqdHTPuZvzffkDq3/9Cwe/+l/T1bxP/p9k2gcREC9+kJOtzOXAAHn/cAj0rC845x7pQFi2yML/jDgv2jh3teZ99BmlpkJoa3QUhIs1OQd2M5syBZcvgzjtr83L7duvleOYZy94YqunFF+TTm5QU+NFle/jNzAoSMrpZq/qyy+DDDy18zz3X+rrXrLFfOkhOtrXBG2/Yfa+8AvHxdgkf+n7ccTaN00+3bpfly20oYXIy3HILdO8O5eXw5z9Ddjb8+79Ha3GJSCMpqCOkshI++QRycy0309Lgn/+Ep5+G8eNttN/mzXDyyXDK0Eriqsqhc+eDz/flFVT7GOJcNXztazahadOsJV5WBqecYk3411+HV1+FmpramXftCvv22dpj3DhbEWzdavfNmGFHXm7cCMXFFuann27TWLLECh8zBr75TWvB//d/w4ABMHnyl1vvFRWwcCH8/e+28jj9dPjOd2yF0VzKymq3PkTaCQV1lD32GPzgB4f+huMJJ8A991hohzP0yist4C+5BH55cxl9e5Q33M1RVASbNtUGeNeusGqVjTn84gtrSf/kJzb28PHHLfT69oWqKti2zY78KSmx08LGxtqmQFKSPa6szIrt0AEmToRvfcu6X15+2Vr9e/da672mxlrup5xixScm2m9Y5ufbPH7yExg8GBYvtnqLimxEzOef2wojLs6mf+mlFvolJfDAA/Db38IFF8Bf/vLlsK6uhl27bKuhKTZvtrXoWWfZvBpSXm6vQyTCFNQBsHix5Ut2tjV277zT+rzrysqyHHn+eRsuOGmSNYq9t2NuzjoLunWz/ZRf/3oTfmKsoMCemJAApaU284ICuPxy2/kZE2MFzp1rQfWrX1mQPvmk3RY+MrNnT+uYnzQJzj7bgvaFF+Cmmw49yZVzNi/vbTRMXt6h9WRk2ObGnj32vK5d4fjjbUVTUWFdQcuWwY9/DD162Ciaf/s3Wwm9+KJtOZx/vnX/dOgAn34KH3wAH39sa8TUVPjNb2D0aKt12TKYNcum3bs3XH89XHWVvZ5337W15JQptlz++Ecb0TN0qIX7jBn2nDVrrMupuNi2JsJvTGamrfz69bOVS90Vy7/+BW+/DTk59qa+954994QT7H0I/6jnmWfam1paal1dAwfa+/D227ZllZNj842JsZVpQkL9Wxs1NTaN7dvtQ7Z4sV1/8EH7sMyZUzu/nBxbMb73ni2/Cy6w13K4XbtsOZx00pc/cKWl8MQTNt8zz4Rhw2wl/NFHcN55tkL84ANbWael1f/ZrKmxxsSYMbYMj6amBgoLrbFQU2OXvXutzk6d7PV++qk1HHr0OPr0wD4X8fG2fOu+tpIS+4ynpBx55V5Xaak1Yo6BgjqAKirse7xzp+VVdTVMnWp5mpdnGbVsmfVAxMdbltQdnt2/v+2PvPxy+1wUFcHSpfC3v1kO3HSTTTc1tfZzU1RkOXHhhfaZbhTv7Yu6a5e1nGPqGXpfXW1flooKu6SmWqt8xgz7Ul17rYVP167Qp48FTXjaCxZY+G7aBCeeCN/7HowaZV+0v/yldh4dO1qr/5prbCE9/LC9wLCsLAvUxYvt/5EjbaGVlFiofe97Fh6PPWYL/nCJiRaO48bB++9b+MbE2Jc0I8OC2rnazaLYWPu/qqp2GlOmWO2ffgorVlhIhSUk2Dx69LCtiD/9yZYZ1O6rWL3adhgfLj7+y2d3TEy05Zydbdd37bLhouXltY9JSrLnnXmm3f7ee7XzO+88ePNNWz7h5Xv55bYyGjXKVoBPPWUr67IyW+YjR9o8V6+2ZbNjx6GnV0hJsel5byvJxETbMe6cfXYGDbLnJiTAz38Op55qjYJnnrHHzpxpW2GpqdZneMcdtkJMTbUvRG4uPProoa+xISedZMc4PPSQdRcmJtqKqHdvu2Rm2udp8WKbf7dutpy2bbMtr8I6vwoVE2Of31GjrGGzZ4+99qoqWyZjxth79Mtf2udkyZJj+qFWBXUb4L01PsvKYOVK60au72R/qan2nY2NtfxMS7OcLCmxvvKSEmu8/va3MHy4fc/r614OZ26XLi3/2upVU2PDFDMzrdX24ovw+99bSxAs5PLy7MvWr5+9UO/hr3+1L9n119vO1y1b7EXWbeWsW2dBsHOnrRx694Z777Uv3M9/blsbVVW2AL7/fWvBf//7Nt3ERLjoIltTgk0jPh7+53/sixpe6P37W5fO1Km2s3fQIKv3G9+wx3z3u7bSSU6G//s/C+5u3aw/bPduC4czzoB//MNWYr172+srK6u9FBXZSqGqyvZ1DB1qK5XUVAvBYcNsZXfNNTa9uXNts+zuu63eiRNt6Gh6Otx1l+2zCAc3WNBfeqkF2KJFFpTFxbbMwivsn/7UutQWLbIPZEZGbbcb2LyKi23lt369ta7z8ux62K9/bQH33HM2z9hYW+b9+lm9K1faMoyJgSuusJVASor975ytZLp1s+d06WJBesEF9v4NHGj9i/v313bJFRXVzrtjR3uNRUUWsNnZ1tLJzraGRXW1ve+rV9vrCw+5DXcTlpbWTiu8AvrFL2obI02goG6jli+3wSE1NfY5HTDAVvgffmif+eOOszx65RX7/H7rW5Yxt95qjWSwhlP37vZd79PHGqYVFdYjUFEBP/qRNYZ27LBMyMiw/Bg3rvFbg+1GOLRTUhp+zKpVFqrhcfRh3rfcztOHH4ZevWxT6mhKSuzNLy210UKN3vQ6zJYtFrj1dadUV8Nrr9kKsX9/WxGABfKjj9rzhg+3raBwF9pbb9lrGDy4cfN/+23rW7ziii9/UMvLbd4JCfbhDx/DcDQ1NfbF6d7d3sOaGlt55ebae3/BBbUr8GOgoG7n9u+3hls4B8rLbct87Vq7FBfbdyMvz/ZDxsTYVl5VVW0XJFhDbfdu+96kplqD7PjjrXGWkmJdxs8/b1vb48dbAychwRpga9bU9tF36VLbE9Crl61kSkqsIdS5M3z72/X3sIi0ZQpqOWYFBbaVnZZmYbxnj43Omz/ftth37bL9itu3W2PxlFMsxBctqu2qLi21LcVu3WzL82hOO822WLdts/19WVn2NybGGjMDB1rIx8XVdgWmpdljwrZssRVMp052CW+JlpfXNozmzrUVw1lnWQOuosLmOXCgRgZK5CmopUVUVlpAZ2VZ+H3+uW3RO2dbt7Gx1irfvNm6VTp0sDAsK7Ou5bIy6zbctctWAl26WDfhbbfZ8/v2te7BrVvteUfTs6etKHbutB2xdXXrZuGen197W7nUdBUAAAi4SURBVExM7dZCp04W4lVV1p08cKB1g48fb12cmzfb1kJ8vA0Y+fBD2wLp0+fQrszhw21ETufOVk94q9t7u8TEWHfo+vX2vF27bOUwZIg9vqzMbq+stNsrK22rIyur4dftvT2usVvwEkwKamnVvLdulJoaa+F/+qkFfVWVBSRYl82KFdbNGRdnY9G7dbOwLSmxgC4ttS7EhAQL5smTbZpvvWVdmikpts9u3jx7TkzMoYE/cGDtPqkOHWxa27bZPGJj7fnFxbWPj4+3Pv39+216lZW1w9eb6vTTrSs3NtaOd9q8uXZLp7DQ5pGdbYHeo4d15WZk2MrnzTftMcnJtuLp2dO6vMrKbKV0zTW24ti82abRv7+tQF55pXZgSYcOtuKMjbVlNWiQdXtt3mzLtWtXew/S0w9dqRyt6917ey+PYd9bm6OgFjlGmzfbyiE93QLswAHb1zZ8uK0IwMI+3Fpeu9bCvbTURtpt22at6/BQ3F27LEBPPtkCvnNn29+2Zk3tKLLduy0Qs7Ls/48/ttZ8bq7Na8wYC+KkJGudp6dbUK5fb2FZUGAjE8NbCwMGWKju2FG74omPt+eXlFiA1x28cCTh0UQxMbYVsHr1lx9z3HG2Et2zx6bbo4e9/vD5x8KXffvsUl1ty+T44+36sGG2cnjnHXve8cfbiLnSUlvBDhxo9RcX2+tOSLAVUkWFLa/jjrNRc3v21B6TkJZml/C+w8JCm0aPHjavN96wrbnw1tD27ba1dOKJ9j4sX24rtsGDbRrFxfaczp1t+ps3W52jRx/7/lcFtUgbUFFhrfLGBEFFRe2O3169am///HMLvIEDLXQXLrQdxqedZuGWl2ejAWNj7Zii8nJ7zoEDtiVTUmLH4CxcaCusc8+1QNu92+aTl2fdQsnJFqJJSRZ64a2OupeOHS3okpJsgMbnn1vre+lSm8+QIfa8bdtsJRneR/LZZ7X7H/btq31tHTrY8qkbaXVH+x1NQ1s7hw9jT0216R0+tB1qt6qOZWe4glpEWo2qKgv+8FkCKisPHWF34ID97dDBHltVZddjYuy+zZtrz3k2aZKtECoqLECLiux6jx423fDWx4kn2gGwK1bUHgn8+ef2/8aNNgoqvNWyfr2F+gUX1G4d9O1rtxcUwNVXH9vrVlCLiAScfoVcRKQVU1CLiAScglpEJOAU1CIiAdeooHbOjXfOrXfObXTOzWzpokREpNZRg9o5Fws8BJwDDAUudc4NbenCRETENKZFPRrY6L3/1Ht/AJgLTGrZskREJKwxQd0bqPM7S2wN3SYiIhHQbD8d7ZybBkwL/bvPObf+SI8/gu7AzuapqlmprqYLam2qq2lUV9MdS23HNXRHY4J6G9Cnzv9ZodsO4b1/BHikiYV9iXNuSUNH50ST6mq6oNamuppGdTVdc9fWmK6Pj4CBzrls51wH4LvAS81VgIiIHNlRW9Te+yrn3I+BV4FYYI73vp6TG4qISEtoVB+19/4V4JUWriXsK3eftBDV1XRBrU11NY3qarpmra1Fzp4nIiLNR4eQi4gEnIJaRCTgAhPUQTmfiHOuj3NuoXNujXNutXPuxtDttznntjnnVoQuE6JUX55z7uNQDUtCt3Vzzv3LObch9Dc1wjUNqrNcVjjnSpxzM6KxzJxzc5xzhc65VXVuq3f5OPNA6DOX65wbGYXa/uCcWxea/3znXNfQ7f2cc2V1lt3sCNfV4HvnnLs1tMzWO+f+PcJ1PVunpjzn3IrQ7ZFcXg1lRMt9zrz3Ub9go0k2Af2BDsBKYGiUaskARoaudwY+wc5xchtwSwCWVR7Q/bDb7gFmhq7PBH4f5ffyC2zwfsSXGXAmMBJYdbTlA0wAFgAOGAMsjkJt3wbiQtd/X6e2fnUfF4W66n3vQt+FlUACkB363sZGqq7D7v9P4NdRWF4NZUSLfc6C0qIOzPlEvPcF3vtloet7gbUE/5D5ScAToetPABdEsZazgU3e+83RmLn3fhFQfNjNDS2fScD/evMB0NU5lxHJ2rz3//TeV4X+/QA7oCyiGlhmDZkEzPXeV3jvPwM2Yt/fiNblnHPAxcAzLTHvIzlCRrTY5ywoQR3I84k45/oBI4DFoZt+HNp0mRPp7oU6PPBP59xSZ4ftA/T03heErn8B9IxOaYAdEFX3yxOEZdbQ8gna5+4arOUVlu2cW+6ce8s5Ny4K9dT33gVlmY0DtnvvN9S5LeLL67CMaLHPWVCCOnCcc52A54EZ3vsSYBZwPDAcKMA2u6LhDO/9SOy0s9Odc2fWvdPbtlZUxlw6O3L1fOCvoZuCsswOiubyORLn3C+AKuCp0E0FQF/v/QjgJuBp51yXCJYUuPfuMJdyaIMg4surnow4qLk/Z0EJ6kadTyRSnHPx2BvwlPf+bwDe++3e+2rvfQ3wKC20uXc03vttob+FwPxQHdvDm1Khv4XRqA1beSzz3m8P1RiIZUbDyycQnzvn3FRgInBZ6AtOqGuhKHR9KdYXfEKkajrCexf1ZeaciwMuBJ4N3xbp5VVfRtCCn7OgBHVgzicS6vt6DFjrvb+vzu11+5S+A6w6/LkRqK2jc65z+Dq2I2oVtqyuCj3sKuDFSNcWckgrJwjLLKSh5fMScGVor/wYYE+dTdeIcM6NB34OnO+9L61ze7qzH+3AOdcfGAh8GsG6GnrvXgK+65xLcM5lh+r6MFJ1hXwTWOe93xq+IZLLq6GMoCU/Z5HYS9rIPakTsL2nm4BfRLGOM7BNllxgRegyAXgS+Dh0+0tARhRq64/tcV8JrA4vJyANeB3YALwGdItCbR2BIiClzm0RX2bYiqIAqMT6Aq9taPlge+EfCn3mPgZyolDbRqz/MvxZmx167EWh93gFsAw4L8J1NfjeAb8ILbP1wDmRrCt0+5+B6w57bCSXV0MZ0WKfMx1CLiIScEHp+hARkQYoqEVEAk5BLSIScApqEZGAU1CLiAScglpEJOAU1CIiAff/eU+GcpDrDyEAAAAASUVORK5CYII=\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ },
+ {
+ "output_type": "stream",
+ "name": "stderr",
+ "text": [
+ "/usr/local/lib/python3.7/dist-packages/sklearn/manifold/_t_sne.py:783: FutureWarning: The default initialization in TSNE will change from 'random' to 'pca' in 1.2.\n",
+ " FutureWarning,\n",
+ "/usr/local/lib/python3.7/dist-packages/sklearn/manifold/_t_sne.py:793: FutureWarning: The default learning rate in TSNE will change from 200.0 to 'auto' in 1.2.\n",
+ " FutureWarning,\n"
+ ]
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEICAYAAAC6fYRZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOydd3gcxfnHP7N7VadebLnLDVdsMDZgqsEmFBsSEkpCC5BQDCmQ0AL8ktBS6IFQAoReHTqmNxuwce+9yLZc1Pudru3u/P7Yk3TS3UknWXIR+3kePz7tzsy+e+W7M++8846QUmJhYWFh0TNR9rcBFhYWFhbdhyXyFhYWFj0YS+QtLCwsejCWyFtYWFj0YCyRt7CwsOjBWCJvYWFh0YOxRN7C4gBCCDFHCPHr/W2HRc/BEnmLgwohxHYhxLT9bce+QAhxqRDiu/1th8XBjSXyFhYdRAhh2982WFgkiyXyFgcNQoiXgIHAB0IIrxDiJiGESwjxshCiUghRI4RYLIToHSk/RwhxlxBinhCiXgjxmRAiN6q9o4UQ8yP1VgohprRx7e1CiJuFEKsAnxDC1lb9SC+8MHLdbUKICyPH/yqEeDmqXIEQQrZ+cAghRgFPApMj91rTJW+ixQ8OS+QtDhqklBcDRcCZUspUKeW9wC+BDGAAkANcDfijql0AXAb0AhzADQBCiH7Ah8DdQHbk+FtCiLw2TPgFMB3IBHonqi+E8ACPAKdLKdOAY4AVHbzX9ZF7+T5yr5kdqW9h0Ygl8hYHO2FMcR8mpdSllEullHVR55+TUm6SUvqBWcBhkeMXAR9JKT+SUhpSys+BJcAZbVzrESnlzkhb7dU3gLFCCLeUslhKubbrbtnCInkskbc42HkJ+BR4XQixRwhxrxDCHnW+JOp1A5AaeT0IODfiaqmJuEOOA/q0ca2dUa8T1pdS+oDzMXvixUKID4UQI/fqLi0sOokl8hYHGy3Spkopw1LKO6SUozHdIjOAS5JoZyfwkpQyM+qfR0r5jySv3WZ9KeWnUspTMB8aG4CnI/V8QEpUO/nJ3quFRWewRN7iYKMUGNL4hxDiJCHEoUIIFajDdN8YSbTzMnCmEOJUIYQamcCdIoTon6QdCesLIXoLIX4c8c0HAW+UTSuAE4QQA4UQGcCf2rnX/kIIR5I2WVjEYIm8xcHG34HbIy6SGzB7wm9iCvx6YC6mC6dNpJQ7gR8DtwLlmD3zG0nyN9FOfQX4A7AHqAJOBGZG6n0OvAGsApYCs9u4zFfAWqBECFGRjF0WFq0R1qYhFhYWFj0XqydvYWFh0YOxRN7CwsKiB2OJvIWFhUUPxhJ5CwsLix7MAZVoKTc3VxYUFOxvMywsLCwOKpYuXVohpYybkuOAEvmCggKWLFmyv82wsLCwOKgQQuxIdM5y11hYWFj0YCyRt7CwsOjBWCJvYWFh0YOxRN7CwsKiB2OJvMUPivKaeuas3MquCmujJYsfBgdUdI2FRXcxb802fvvYuy2ODeubyws3/xy3w56gloXFwY8l8hY9nov+9iLrdlbGHN+yp4LTbnkKXzCMNCQDe2dx3xXTGdavrR0ALSwOLix3jUWPJaRpHP3bR+IKfCP1/hCGIZHAjtJqfn7PK5TXePedkRYW3Ywl8hY9lt88+g4hTe9QHUNK7p01p3sMsrDYD1gib9FjWbJpV6fqrdle3MWWWFjsPyyRt+iR7M1mOP1yMrrQEguL/Ys18WrRIxFCkOFxUesLdLjuH845sd0yJZV1XPnwm+yqqEUAJx02jPuvOrMTlu4ds+as4OF3viUQ0hACCnplcdYxYzjliEPoaz2sLDjAtv+bOHGitBKUWXQV89du4zf/frf9ghHsqsKtF0zjx8eMabNcSWUdZ9z+34Tne2elcs/lZzBhWL+kr90Z/jd3BX9//euE56884yiuPvOYbrXB4sBACLFUSjkx7jlL5C16Mqu3FfPLe19PeP7m80/i5MOG4QuGKOidnVSb0258kiqvv91y918xg5MnDE/a1o7w2ZKN3PLfj9otd87xh3LrBdO6xQaLA4e2RN7yyVv0aA4d3If+uYndFqdNHEleZmrSAv/sJ4uSEniA21/4JKlyHaWyzsdfXvw0qbJvfruaZZs7NwFt0TOwRN6ix3P7RfF7ssePHUxGqivpdgzD4IkP5iddPhDS8AfDSZdPlq+Wb8HowAD85S+XdbkNFgcPlshbdBu7ymuYvWAd89ZuR9ON/WbHkSMG8vjvfkp+VipCCJx2GxdPO4J/XfuTDrWzs7wWvSPqCthtaofKJ0NI0zsUPbR88+4ut8Hi4MGKrrHoUirrfHy/bgePv/8dJdU+XA4bqqLgdtp56rpzKMhPzi3S1Rw9ahAf/e2KDtWRUnLfrK+ZvXA9KU47vzp1Uoeva1O7vh91/KFD+Pd735HsOq+GUIh/vzePt79bhaYZHDe2gFsvmEaq29nltlkceFgTrxZdxitfLuOBN+fGPScEDMjL5J2/XooQYh9b1nGKK2uZfvuze93O0sevS3i/UkpWbythW0kVu8sqePnLFRw3poB7r/5xu+3+58PvefaTxYSTUHqbqsSMpFKcdj7/51W4nVZytp5At0bXCCFGAG9EHRoC/BnIBK4AyiPHb5VSthkOYIn8wcvGnWX84m+vtFnG5bDx8i0XMKRPzj6yKhZNMzAwcNjaHsROvOahDvm943FI/zxev+2iuOd8gRAz//UW67eXEE+mrzljIr8+8/g221+3o5TZC9bx5fJNlNc2dNi+IfnZZKU6Wbql5QrfGUeN4q+X/AhFsby5Bwttifxeu2uklBuBwyIXUoHdwDvAZcBDUsr79/YaFgc+73+/tt0yUkIg1PUTkbHXkfztlS94a96apmND+mTREAhTUm0mH0tPcXLvlTM4csTAmPo1Xv9eC7yqCP7085MTnn/wrW/YsLM0rsAjJY9/tISCfr2ZNuGQhG2MHtSb0YN6c9P5J3H1w2+yaOPOmDID8jLYWV4bt35hSVXc47MXrmdrSQWv3BL/AWVxcNHVPvmpwFYp5Y6DYUhu0XWUVbefuTEY1hjWt3vS+O6prGVXRS3Pf7KYBRuKYs4XFle3+LuuIcjMh9/i7stO4+G3v6Wi1oeqKpwyYTi/+fGxnbZDCBg3uA+3XjCN4f1yE5b7eNF6ND3BkyTy27np6Q+ZeWYVV5xxdLvXfex3P+WZjxfy2lfLqWsI0j8vg9sumMayTbt4+uOFHb6P9TvKKa/xkpeZ2uG6FgcWXS3yPwdei/r7N0KIS4AlwB+llNWtKwghrgSuBBg4MLZXZXFwMLx/Hl+u2NJuuS17yhk9KL/LrltYXMmNT81md0VthzNOSuC255pj2TXd4OPFG1mwZnOn7fn8H1eSne5pt1xYSy7a6KnZC5g6uoAhBW2/Z6qicNX0yVw1fXKL42MG9uaZTxbSGa/sgvU7OHNy26t/LQ58uszpJoRwAGcB/4scegIYiunKKQYeiFdPSvmUlHKilHJiXp61WcPByplHj263jF1V9toNEk0gpPHrB2exvaSqwwLfRBz1q/Z3LtwzPcVBiiu5iJWjRiXXodGDYS477jbuuvmFTtmUmuLk3l/PQOnEyPpACsqw6DxdObNyOrBMSlkKIKUslVLqUkoDeBo4sguvZXGA0ScnnVMnjmizjNvpYNTAXl12zbkrtxIK63RaiqRsco10BXUNIY75/aNc++jbGEbbD4pbzj8Jj9Me9yHTAkWg1geZ+9BHzPlyRafsmjphOIv+/Tv+cE7bE7mtEYrlcu0JdKXI/4IoV40Qok/UubOBNTE1LHoUd116GteedQzpKY6Yc067jfuvmoHahREb5bXepN0ecemmeaPv1+3gxqdmt1mmf14mH97zKwaneUyhb/wXjW5gK/Wi1gdBN3jxwQ86bZOiKFw0dSI/OiLxRG5rhkZFQdX7g7wzbzVn/+W/TJj5EBNmPsTUGx9nfVFpp22y2Dd0SZy8EMIDFAFDpJS1kWMvYbpqJLAduEpK2eZuDFYIZc9BSsmSTTtZtGEnOekpnDppJFmp7i69xsrCPVz90JsEO+uq6UYEsPSJ65Mqe9ZRN1DVEETPcBEanodUFRAC+55aUr/chBLSCRRk4ps6AtVh41enTmJ0QT6DemczqHdWh22bvWAtT3zwPcVV9XHPKwLGFuTz/E2/AGDl1j3M/NebBMLx3+fX/nQhI7pwhNaaVYV7WLJpB0P75HHCuKEHxTqLfY2VhdLioMUwJGu2l+ALhBg3pA8eV/MoQUrJT+94gR2lMfP5BwSLHv09NlvsyEU3DNZsKyE9xcXgPtkEg2H+efvLfP/6fPSwRjikoQTMfwCVv5wEzkiMRCuB65WZymu3XUhWakqH7QuGNeau2sotz8QuX5lz39Wkp7rxB0OcdMOT7c55fHXvVWSmddyGRGi6weX3vcqaHeUx56aMG8qDM8/qsmv1BCyRtzhg0TSDuoYAmamumMU3hcWVnHvniy187lMPH8Z9VzZvznHd4+/yzept+8ja5FEVweLHros5fvqtT1Fa7Wtx7NVbL2TkgOae8B9++TCrXvseNIOGw/oROHJgm66l3lmpfBwnZUNFrRebTSXTk3gEdeS1/0JLMH+w7Inruenp2XyxrP1oI0UI5j4wE0+rVAm/e/Rtlm3dw9TDhnLHpae32w7A7ooazr/rJRpCWsIyvz/7eH75o7ia9oOkWxdDWVh0FF3XufPlz/ls6SaCEReAoggumXYEvzvbnBw0DMk5d74YU/fL5Vu4742vufH8kwBw7edl+Yf0y2PT7tje5kVTJ8Qcm/KHx6nzB2OOX/C3V3jrLxdzyT9fxxcIQwoovzoaQzdM30k7lFZ72VNZ27QT1Ncrt3DDkx+0eDjOnHE0V7QKr5RSJhR4gFe/XMzXy5MLJzWk5PbnP+GhmWZKho8WruP255vTIX+wcAMfLNzAizeew9ghAxK2s6qwmCsenEW4nYR2j78/zxL5JLFE3mKf8dSHC3ju00VNwh6NYUie/2wJZTX13H3ZGTz+wbyE7bw2ZwWfLNlIdZJ53bsDl13l9z89nvOnHM4Lny3hqQ8X4A+FEQJGDujNZacdFVMnnsA38rM7XmrxtwHQgeRmO8tMkd9VUcMfn4ydoH1i9gJe+3o5X91/TdOx9lww97/5XdLXB1gcteI2WuCjueS+N9vM53Pny5+1K/BAUmUsTCyRt9gn/PXFT3n/+3Xtlvto4Ua+WboFvZ0MvftT4AWQlZbCvW/M4d435gA09ZqlhPVFpUz54+P87ifHcWkkc+XrX3dvTveZj7zVbpkaX5Db/vsh9/xqOgCOLk6D3Jg7//u1bbvPVmzZzeHD+8ccr28IUFRWk9S1PC4rsVqyWBmILLqForJqbvzPB1z491e59/WvkxJ4AAR4NQ1/MLE/dn8jgeKqemTkdaJZrUfe/Y6GoNl7X7m1ZB9Z1zYfL9nUlJGyq6fjJDBh5kO8P7/taOndVXVxj9vbSRoXzT+vmN4R037QWD15iy7nw4Xr+b/nm9MFdDiWWohI3Dhmt/kg5vQ/PU29v/uTsnWEGq+f3AwPx133aLe0/+myttNbjBvcJ+5xl8PGCYcO4ZvVhW1uMnPbL07mmNGD98rGHxJWdI1Fl2IYkqN/+0ibE3oHLj3gqXKAYFcE4QQ5LI4bM5hHfhN/V646X4BrHn2bbcVVgMQf0rCrCiMG5PLItT8ls4vXWvQUrOgai33G6m3FB57Au3VQJXhVEot4os6OJfyd4aWbfs7P//Fa3HPfrd2GtyFIakpsnp90j4uXb7mA9UWl7KmoY3j/PAb2yuxuc3s0lshbdCn2OIt/9hspOuqkWkjTQYKssWHMyyS+aEtzhsogwXmLjnD5A2+0eX7j7nKOiDP52siogb0ZNbB3V5v1g+QA+kVa9ARGDeyNw971m1d3HIl6bA2k6wgVhA3w2cwefVxEgs58TxL8feOatSmChnDbo7ny6vgpFSy6HkvkLboUIQQPXt3GknPdwFZSj1ru7frwjmg78sJgl4job7irLeERIAU9S9T3D1oS+aRvfe4TJsx8iBc/7/gc3JyVm/nlP1/h25Xt719gYU28WnQTK7bs5vIHZrU4Zt9ZTeoXm5oiZ6TTRv2pI9Hzun73IdE/gDLOi7A3f7+lAfrn2RBQSOiyMWt3uT0WifnqvquTmlCtrqll6p9iN1efe++vSUtL6w7TDhramni1evIHCfNKvuSdrf+lrCH5cEQpA8jQYmR4/T7fAKJfbkaLvxVvkLTPNqKEdJSwgaIZqL4Q6bPXQjdkkZTVdlBa3rNQQJlcA/Y2XDaWwO9zrv6XuZArEAhxwvX/bkpl/NBbc1uUiyfwACfe9Ey323gwY028HiDous6ts2bzzdJtSGDKpMHcfc50NtWuI1B1NYenVKG5FJTqB3huy/FcNu4/TXWDgRXUV91EGkVIDGyidcoTG6j9IOsZhG3QPrmfvMxUHDa1aem8Y1M5cbeFkhLH9mpCwxLvh9opfCpylxP6BU1/PCB1052Ebgn5gURJVR0L1+1g5qNvtzj+0hfLePvb1Xz78G8IH4DppA8WLJE/ADAMgxNvfYyGOo3GnuRn8zczd8eDXD75e6ZlB3GlGkRCPzgv5xte3Xg/F4y4gS92vsdHRe/gN/oz3uPiV/kb4vRFNQxtB0blRdh7zUWI7h/A+QPBFrlRFH8YEUfkhSERwe5ZLGSsSENUORAFfoRNYux2Ire6wbBE/kDCHwzHCHwjvmCYbXsqyEpvO41xKBTC4YjdrMbCEvn9hhYqorbiUjLELtbs6oVWfya20gAUBJEngayxE1yaxhNvHMcTUqCmhTn5lPVcP3wZbkXD1zCXc77axuGpFVzffyPpagi3oqGI+FlpFQF+rZItFR8wOu/H3X5//5w1p8Xf4f4ZuDaUImJ2chJofTLoHgSyyIUscnVT+91Ao1vtB7QxRnvJxs69+yU+uPPyNstYAp8YS+T3A4bRgFH5IzKFgRDwypsFeJ5bgRAG4UluGib1xViYATqIXkFEQQApJN+uGMy4vDJOyy7i/F5bOT27iD4Of5MetLdlqUDyzo7PGJV7VrfvrhNo1TsPD8hCy0tFLfeiRIRe2hSCQ3LQs7tus4mDnsaUDhZNGBKm/198fzxYsyjtYYn8fqCy6m6yMQW+uNjBolVOQtelkDsgxNFj6zkmeyHVI508VTKaBhwR4ZY8cuwXjPFU4VRMkfQoWgtRb0+3HYrB/NoUqkJecpzdG41w47kn8Vn0ZhOKoG76aJwby3BuLkeqCsGRvQkNzUncSFfQxZt17xMONnv3M9OPHMmt//2I86aM57Ch/dotv72kiqr6BkYM6NVip7GeiiXy+xApJW/vXMQzm0JUaz8lxxagzmsjeK0NxQZ1ios5/kzm7u5Prt2PLpSmXsrolGpGplQ3CTwkpwXRncL5tfnUaC7cavd/sXMyPRxakM/q7VHZF1WF4Oh8gqPzu/36Fj8cZi/aAMAnSzZy5IgBPPH7n8UdqVbW+fj94+9RuKcSm6oQ1g2uOXMyF5/SszcfsUIo9yHPbPmSf657j0rNgYFCuZZCwGkHm4KBgt+wE5IqQWljdyiVUNQzeJirttPD0u0bnYSkwj93HclxvUaSYovNGdIeUkqkUYuUoaZjujR4ffN8Tnv+IaY+9QAPLPyYoN7spnnh5l9w6y9ObrPdUQPzyG1nUm2v0PQfnvvDkNh3VOFcV4Ja6Wu/fA9i0cadzF4QP631H554n3U7SgmENbyBEMGwxkNvf8sjb8/Zt0buY6ye/D4irGs8vfWrmONmjyNeEqyWf+8KeTA6IfPBAHz6RhaFlwxlUPoh/N/Yn3W4DRn8Dln3Z9BLAAXpPguR/mcuffdF1n7ZvDz9lZXreWf+GuZe90fUSATPOSeM52+vxd53I8eNHcyQPjkcO2YwAjj+D4932L42samdc3+4dZQRPkRuGBlQkJtTkKUdfzi2YB9Mqip1AdLfX4MIaQgDEBDqn4n3lBFJbSXYE3hy9gLOnDwGgIXri7jvf1+zp7KOQII9Y5//fDk/mjS6xT67PYkuE3khxHagHtABTUo5UQiRDbwBFADbgfOklNVddc2DiYWVbS3Bbv/Ht9ybR2nIzQCnF3tkkY8h49ds1JBwCFbNT+XdD/rw9H33Mig1r8N2hwJr+G77HWwLpFIeHktF2MUA5waGOmew9qvTaL2FU8NWldtnv8ffzzy76diwPtlsKa6K2/7THy1qen3MqMR7f3aaTgq8OqUabGZaBOExkBl1GOs8yG17MeoQAuENonqDaPnpnW+nDVIWbEc0hFAkGCl2pKpg21WDa20xgUP7dss1DzSKq+o46YYnuPSUCfzr3flJ1bngb6+w7Inru9my/UOXpTWIiPxEKWVF1LF7gSop5T+EELcAWVLKmxO10ZPTGszevZQ7V7e/RVsjKjoSgRHlUctQg/xpwFKOTS9GCFjfkMULxcO5LH8jBU4vfz6/P6dfUMPoiQ3U16h88HwOX7yVjRzam883PNYhe6WUPLv1a17f9iEhqeA3GvsDAhs6dkVye68lPPvNBDZnekCRyG1u5B4Hat8wd532YyrLaynzBhg3vB8PvjmH4ipvh2zoONHf5c73WpXx9YiBAVovJ5Aa6B/n7l2cvT+MUAXS0dn+VRupj6UEzYCwjhLQMNJdICVKUMO9qAjfycM7a/UPhjOOGsXdl562v83oMPszn/yPgSmR1y8Ac4CEIt+TGZne/qx/4w/YJTRGuavIsvn5qm4gjT/qWt3JLduPwSYMVAwCuo1JOUM4dJi5CfTkCz/m3t8920LrjAwXj826scP2/m/H9/xnyxco2Fs8aAA0VDQD/lwyiUPG16D6bUgUZE49BEBfn8Kt774PVXbTlq+Wg4C8TA/3XXEmizcW8dj7yfWwkic674wEEdlZqhNiL3JDMQLfdAmPDvWd/NnoBmqtHz3H07n6pnWmIQIzbYMqIRQZTQkBdhXsKobb3jSKMewqvhOGdP6SB2OEUif5aOF6/MEwD1x15v42pcvoyolXCXwmhFgqhLgycqy3lLI48roEiEkQLYS4UgixRAixpLy8vAvNObAYlpZPlq29ob7ALcL0c3jZFkznq7pBNItU846imhQENBvjUwbx8KRLm2qfd+3pvFvzPEdfeTL5U0Zy3G9P5YNdTzFqXEGHbH17xwLu3zAbkDECH42Oynp/DjJioxCAC9RDGxBDGhD5QfNg5BbKa3zM/NebbC+N77pp5JjRHXXbNPZuG9+rSNpgR+c2L5H+BKmSFSDYgZ+MlM1++LAOAQ2hG6YQ7xUC0jXUybWIMT7iphBuLcqKFWORLF+v6FnZLbuyJ3+clHK3EKIX8LkQYkP0SSmlFELEfBullE8BT4HprulCew443jvpJk74/K8Jz0sJDWE7W/TMOD1JyWGiipLSbAZ6xvGXaWeSlxEb656a5uHuJ2d22sYPdy/lvg2zI38l23trLicESBuIkAIFAWSJs8X5QEhjyaZdbbY2vH8vHrz6J3y9Yit/evajjt1AtE0hBQwjInCND4L2XTpycwoyq7Yp5w2YeW9kmcNsMykivV/dwLanFrW6geCo3ubq3r3uGUtEdhiRo0G1PbkqezPp+gPpxfdUukzkpZS7I/+XCSHeAY4ESoUQfaSUxUKIPkBZV13vYMSlOnj5mN9y2fzHCEfy0ERPichagfAYzTG+Ue5Xt+Lkj0f/lRHp3Tt59uTmL9Dl3m3fJwTQO4T+VXarMxIJlFa37Zu/9szjsNkUJEnY0Z5gNr2/UWXyQqY4aglEvtyOsToVZazPdPsIkKUOjGUdmCxtfJ5IcGwpw3/MkC7owTe3rRQEkGEBqQfWJuFNSGk+4Iqq0QZmQ/SOYVJC2AC7sl8eIE4Vgj+gfGddIvJCCA+gSCnrI69/BNwJvA/8EvhH5P/3uuJ6BzOHpPdh3ml3s7m2mG/L11MaqCPHmcq03FRKq5+mPriDObUDWFLfh4C0k+1M48x+E7hw8HG49sEiprJAbZvnpQHGZjeyMMUUyeww6lgvIqP5VyMloAJ6Yw+6kbbEOFJO05ly5QM8e+el3PbsJ0laHX8yUiAZM7CMNbtbLb7y2lCOrTHz2iSIlpFFbvSdLtMHH1QgnLy7QxEGttwgoXI3qILA4f2RXbktoktHX50KlY29+AOwpy0EqAra4Bwcm80MpKGRzd5aW0kthsuO0avrVl4fNrQvO0qrGdQ7i5vOP4lvVm3hydkLW5RxqArf//v3AEz54+PUNQRj2umduTdzJgceXRJdI4QYArwT+dMGvCqlvEcIkQPMAgYCOzBDKBM6ZHtydM3BQHmtl+nz/9amZujLU5G7nREBBzAn/9STqhGe5p639Cvon7WXskA2/xfdozOk6cN2ttMHaerFRwLC4xh+/pGr2FSSy/Ki6BGQabNyXA3GyjSoSdLlAeZEZ0bYdNt4FWKntSQj+5Rz0rEbeeLN45NvN2kk2GRkFNLqfqWMxNXG5Jrev0iJ8AaRbkdzj14zTFdap6OMYokOgbzygddZsqW4xflZt1/IsH7NsfCBgMbUm5/AHxU/n+Z28OW9V2GzHVxLiLo9ukZKWQiMj3O8EpjaFdew6F62e8u49MNnkFmJNV4GBHKXq1UIoQADjC0pqOOb3TDSm7jnmp9RxwPnf8Ih+ZVc+NQ5bCppFb+vCHAk4dpoejAoiIgrKBq3I8SRQ3YxsWB3K5EXoIOxyYMY6EcmK/L9A6jj65FhYW4IrgiaPUoSRRicM3EtN50xj0ue+SlthjvuDfEEPpp9oe8dWdglBDK11UIymxLZbrFrcNpUarx+bn/uY+av2xG3zHl3t4yFd7lszPvXb9ldUcP8tds5/tCh5Gf3vB2mDq7HlUW3sK52F1d8/x/CWXrbv1mvzQzbax0nLgWypvmrJCXInfHT+3qcQV789VtkpgQQAooqM+Nfq4O+2nR3gKBmIxC2R6ob+EN2bnvzFI4dHu9HL6DSZvq1k0IiXDrCBsZ2F/jVmIedqsA1UxdRUZ/C5pIcukxtWwhqW+IuQE0yJene0tG2uzm75nt3XM70255p0SuPx9fLN3HS4Ye0ONYvN5NzTzys22zb31hxVT9wQmGN2+UFvjMAACAASURBVL57lTB6k37IROlePHr8hUBCItLNH5c0QFbYzO334jB93EZSHOGmiL78jK5ZIBXSVK4/ZR4j8stRhBGxXxDQ7MzdOLhlYZcOOSFzY++KZF01oim0UpY44r4PUsKVz5/FOY+dR1jv5CSrISGkme6MkIZaXIdjQ1n8XbXaa+dAy9nT+sHQRQ+hw4f15Y1vVrQr8AA3Pf1hl1zzYMLqyf+A+XL5Zu7647M0/BEaFV7f6USu8aCeFjt1ItwGIj9ohkVGi5wCyjA/stKOvijddGEkiFwZ3bccl6N5knbmSYv4y7snN/XAAVOgdMMc0icpBEHNxk+O2EBdwMX2ikyCWnN7mtG4WEiiTKhD9AmZ9qsSuduJsTytfdeBkCh5ZiSLcBoR51DLOpqhRlxPnRevtNlrkE47an0QW6UPLcNF7fmHd1wQE+0e0wPplZnGd6sLkyqrH2DPvX2BJfI/UHaUVnP7k7PxfFuIuLoAma4i61TkyjRzD9QGgUyRsWtqJtRjrDOQO9xmlqJUHeXQenAZ6HMzoyZk47O9IrOFJ2Hq6EL8IRuPfnE0lfVu3AuLcK8rAd3ASHXiO3Yw4UGtQzFjUSJLMNYX57UQ+BZlRvkQ+SGEijmBCtAniGhQkRvaiagQEvIDZjtDAuilTvP+Ywu2a2tbNBwxkJSlO7FFskf6ju7knrwHgsDvo5Wyny7ZiF1NzilRkNc9OYMOZCx3zQ+Ut79bDburkYrA8X4NhA3T1xwRLn1jfNETKqiH+lBOrYDcMPhV5B4nxrqUpCbSXpo/nmqfs4UnYfr4TTz/q/fwfFuIe10JQjMQEtT6IGlfbMJWUtdcOIELQjNU1u3J45D8Cpy2eMN2iSgItFjgBCBsoAz2t2s3hkCEFaQGIieMGOU15yfirTbdC/S+6dTPGINvkrnq18h0JxbK2LWFBxb78EHT3haCjfxq+jFNr32BEKsKi9lTWRe3bFjX6arcXvsTqyf/A6WizoduUwGJ8/Uq9Fwbek4GTT3R3S4Y5435hkgD0AVyXUqTP9vs1Ud8+jERhS17c7q0ceoDl/LMZe8ybmApSPh6/TD+8toxuDevQrQeT2sG7sVF1M8YY7px2ggNvOeDKdx//se8PP8wQpqCJCrME8zQw3gkOt4CgT43CzHYb44GUgxkZhiqunjtQiQNRGB8P1zryxC+EGTEEXq3ZoZx6q3fDxkbktoa3TA/l8be74HQ6weQErXCh5ASLTe1y8NAL5o6gTOOHAnAs58s4umPFmJXFcK6zrghfbnnl8dzzp3/oy7QcoHZTedN4fwph3X7lpndRZdloewKrDj5vafIW87L2+ewub6cUem9ubS/jVx7CBxTUGzNoYqfLN7AXS99jvPZ71EawgggcGgvfJOH0JhTQQzyo4zzQiv3rvQqGDtdoAlEfggcBu4HyvGNGxa7qrMNYb7hnOMpKarg5e/XotYFSH9nFUo4tkcmBVRdepTpo9f0NmOrc1J9TB1VyLIdfdhalhORd/P6ygnVKFmxvXyjyobxbVbCNruMxjj2ZFwLUuJcV0JocA4yJc6DxGaYtxVuFXEjZJsjKuELkfXaUtM5rQgCI3vRMHmwGZWzr0UsqgOglHux76klPNhcW+HYVEaoTzpGvwTRV0nwzf1XUlzjp6zGy6gBvciObE7z1Yot3P7cx63yy7fWwZbvxc3nn8T5Uw7cCJy24uQtkd8H1JTX0lDnJ39wLxRFobLOx/LSHazVdlAWrOHQzEHM6D+BVFv8sMNkMIwQJcU/JxDejk1IltbncWLmHuzCwKVoZmSdczpK1kMAhDWdy+57g21ri3C9s8oUT0Whfvpo9LzU5q98VhBlvLd5oVOcPThEcZi0mTvwHjeMUEF2s9CHddSqBvTeUbHH2SGUQQGwS/oH7ZQudxJUVAjrZL+w2Ezg1QoJNBxTQGBsH9zLduEf17fNFAG2snqcq4tBNwhM6G9mfRQCMsOox9aAYj7HGr/6eqET1qaCTJR6sovEL6Rj31xGeHR+8oKayK8tJMqxNWaqhaBoWgumTKjHWJie2GZDkvLdVtzrmzOM+CYXEDi0D2gGju1VKIEw4b4Ze5ktMwka7y2so9b40bNSmkNANQNbhQ8txW6OZDrJ0sevi+mBX3rf66wqLE5QIz52BRb8O7atA4X9mWr4B80XS9dyx+dvEsgPo1YY5HxQR/ao4Ww8vApy/IhKDZlr53PPah7d+DH3TriIyTlmzm+lo1kDy04gV1QhIp2+Gdm+mA6jDH5ITbnElX0vTtXOTRefwH/eX8Cm7FSc87eRVhPgBCWF3hNHs7CqhpKGGsr71WDMy2pa1q+M8sIQfwvftlJuDm9Tv9pMaGgOwRG9AIFzUxlKjZ+6n5nr5MRwH8ohDU0PihIjiCe3juBXvcCuEhyUhbOwEgEYThuhwdlIm4pjZzX2nTUEDsnDvXQnhkMlOKp309L5aBwbykidV4ihCGrPOwzpak65S40d/csslBF+ZIaGSNfMOYYhQRgURBa6MdZ7aBZI2er/qB+4Ks3edFAh6YeAKnCvKTFFvj0iuV8Ac3ermLYkIltDnVYF9arptsnQ2rdHEfiPKsC1oazJpR/OS8VWVk/aR+vN1amRXn5wSA6+KcO6r4cfaddWWoeWlULKoh1IRWCk2FH8YYIFOTh21hDaC5FfvmU3E4b3b3Gsqq6hw+2EDdB0A3u8z+IAxxL5vcTrD/Le/DXMXrmGnaEKgiIIXpUU3U3DpFI4VCJU0HtB2ch0yjftQumvYhcS3WNnYH0NyqdetvxoINfPe470i7chfAbuVBcPzL2T4YcPbvP6mt7Att1XIjWNoVGu27gDNAmp2kfM+NKgSjd76yJbI+3VIgJ1BkFNMm97OY6PlnHjc7/hxHPP56Xl9/HwymaZMzZ6UNI1c9JVAjbQs20QMhMOO7dW4txaaV5OEfgP7WNWdBooIxrMyJbGthRBKBUzLLPYTXBcH5zbKgn1z6T+lBFmIQENRw3EVlxH6jeFCAmp87eTsqgI/dRRyGF5+IIhM4xcDZE6rxChGQTH90U6bbGukYANY2Uaon8AMcHculAI8z4Y6je9HRsiQq8YiCk1iLDA+NwDTgfYIpuK9I3kPAkJ5AIXRo2nXR+yCOvYav3Yt1WaEUPRtkV/YIbEM2cz9pJ6wn3S8Z00PFZoU3TQzYlj0s3ZcqmBsb79naukItBTndjqzXvQs9xkzVqBEooKFzIkzsJKfCcO7QKRj/OQjELL9iA0g4ajBkW+U4q5RqDGjxLauwRsC9YXxYj85NGDePu71egdXHtwMAo8WNE1e0VVnY/pf3mGB96ZwyZtF8HRlXCoFzm5Ft8hFeCQTaImFPMHKYfbMVSFoGJHEyq7MzKYfJGf+zO/wSYNwkeZQ2S/N8A1E28iGIhNoNRIYflLeIsnka8uY4i7ZYRA3BF+ZFR/Xq9CRnuqGOupxP1mFaJOR2jmF14akmBDiAevepI5O97k2Mx3OHLgLkTj+n1DYCzMRP8mE2OtB2WVm0m+iYh4USaGJDCyl9k7zAkRL6lkEJWCsabrQMtLRcv2mAIf2fwCm/lP659p5rMBDBvU/2gEdf3SqQ9EBB6J3V6FjNx4uF9G/B5w43uRH4x1O6mgHOJHHFcNdh0xOIiaZqBkaagT6kHXUY6qQfQNIlSzvHBLlMk+0r9fiWgIxb8YQFjHvWQnQkLa11uwb68yFzxpzcIqGsK4Vuwi69mFuLZUovhC2MsSLBars2MsT0P6FHOFsV/BWJWK3JlEr9emmJvH2xQMu4qt2t/CjiZ7NAP7zpr220uaBKLqtiPTXeZDrzG3jcOGnp2C4Uy8WE0IsLXz/MnwxLpA01NcHRb4v158SofKH0hYPfm94OZZ71PvDSIK/ChjG5pzwEugtxa/A9TqWFDaeLdqCL8avZZLbBt41RmVx0XCo9c+ww3/vTammUCohOzgP0i3Jd/TkRJ2BFI5J6+Qc/PMxSPXrhhGsRa7QbUv4Ofmt+ejbD4KpUxHcdahp5vRNw5VI+xVcbnD2MZrrPSso+99g6m6aXuL37EEZJrL/DUmWByFLgmt85uCZ1OomzE6of3BcfnYgl4axvY3Rb/VG2zUpiAiPWK1NoDWrzGXfMw7gVFpR+kXX5SFADEuKrOmEIgCHVvfSmSKEvu5OgShH2eQ8ehqas49rOVCJCFMP/i8QtwbzU1xhGaQ/sUmtBQ7DccMJjw018zvkmInOLoP9i0VhAdloQiDhuGJ/fdyjwt9j4sOzxsIQe25h6FW+syHu0xc37W2JKl1Cu1csF174mJTCQ9IPCEuJbz+50s4584XE5Y5deKIpte7y2v48Z+fi9PXiHf/zaOPXlkpnHXM2ITXONCxRL6TbKkvYenGXYhBoZYCTzuj2zjnfLqN/349CewGtuUte+4bF2+N28zGXVczxJl8b0RGIusGubwt7MvM0igmVuTRIPW2PaBLhCFxi1LCIzzUTxsBYUG/4ZWUjIwEd0jYPsaOeHEw6vM6otog3D8TLT+t6c2Q5Y5I1Ecrm8MS33NeMsqXU3vhEeBK0HMTEJ6UQt2pIzFWp8V5kwW6Ow09w4la5ce9toTgyN6Jx6qJjktQsnVk6zw+NgF2EV+uFIE2zIPwlpD65Ua8p40AjWZ3jCIw0lxIm4LQIvsI2BRwO1oKqBBIh0r9OYc13XNydMKdIgR6bqr5WjfiNmHYFEIDs1AqfBhZ7lj30j6YhJRpcb6bUdgUlc//cSWn3PJUi+MCeOQ3Z5OTnsIXyzbx4mdLWLOjNEEr8QReoAKLe8Dm3pbId4KVVdu4YtHTqMcAro4FSqBj5lqPPo7gu/o+7FiXh3ayTsZbq1CCZnjXsDg+eWlUEdIrYo63RdQufC346ZXl3H+9i2BDs1FSNW0SAT2qjsS20Yf7yCJCBbmUDBYxi3Fkjg3tUifaVxk4CyuwF9ei9Uol3C8TEOjzM7AdURVZRATYBK7/lKNuM3vUjj1VhPo29tziWFvqwCh2NddvjQH1Z4wk/f31CG8Qzzdb4vuzFVD7x7rBpATZIBCpZvv6AvNhIkZ5EWmGuQ+Ijrkwyt5sgzRA1rvwHzkQZ1GJ2ZNv5Z8PHDEAvXcazrXFKEGd4JAcgiN7tdxMAxJ8mdr2ae81qoJ32gjSPtsQmfCV6Lke6qcdgpHiAAkipKFWNpgjqIR2dgPtXGfNjmLOOHIUy564nrCus6qwGF03MLZXMucf7/Po1j3s7pWCLz+1zbYUASlOBylOO+dNOYyLTzkCuxrr7pu3Zhu/fezdFsd+PuVQbjp/Wufubx9giXwHqA01cO43D1KjRWbnOyDwEPmJ2mOHhhLBtr52tFV2cKv4x/XBs7gIEFz3n6tiG9Ir6OcMYRfJ7+AkJWxoyGBESm0L/Tl+Ri1b17qZ9WQvNJuK0CV6jgO1JNhkZWhAJoFD+2K47ajb65CnaeCUcSVHFAXIemUzwpCgGUibgp7roW76GKi147m8CIbZkE4F2xo/oqHxHiRTjGWcf3oxu529eX/FKEKajTW7e5n7zEqi8uU0jghiLTBS3NScfzhqhRdFBkGEAXtUWWmmRrbpyE1ulJwwIl0HAzOF8JxMOLUK6mzIUtOfK3JD4Aqir0gzk5MBeHTUw+shUwNdYBR6CIz2oLjqEy5GCvfPJNwokmEd56Zy7EXVGKlOgqN7o3hDOLZXYThUQiN6mSGFTfcb9UESv/02aafnHR6QSfXPJ+DcUo7whwgc1h/psDU9rCQqWm8VpaoBIztqcnc/b/J95Ijm/YDtqsoRw/vzr2ue5ouX5hLwmQ9yp03Bd/lRbbaT4nLy5X1XxRX2Rp74YD5Pf7Qw5vjrc1azvbiGx687p5N30b1YIp8ktQ1L+Hzr7ZySnsr/qoYBcXyz7RGn/LHpe7iu70oGuHxUj3Xx/HeH83rdMFhcxC9uGInTFW8hzCDy7AEW1uUyOb0sKTtCUuG/JaO4q2AxbjVqsk/ABTeVsXjaEFatysDItmGUu0i/awsYBg3j++I/YkBTXLqe5Yb5EuXEaoSruTer73Ai13oQ1Rr1p6SQsmwX9uI6M0VBuQ/XmmICh/VDpjiwrfTFfUCs+cqJLZTLzf/exiljthE2FIKajRs+nMrKdf1p6WOJFvrG/5v94HpeGjqpcRYHmVEz8qtskAKjqU7kXlQJxU6MTc1CJssd5uKvOltzW14b+vwMxCgvcpvHTD2sGvgP7dvuPrAipJHx9ioUXwihGUjAtc4cAQhdIgW415TgO3awGSoK4Avh3F6FWu7FVu4lOCa/OYw0GSJzA21FAEmPg8D4fs2hm63LClBrWok87B+hlxJVEeRmpLY4vHXldj5/YQ5Bf/N8S6OLrC1uPPfENgU+EArHFfhGFmzcmYTR+wcruiYJjMqLSa29gLNzC+nt9OPsQA86luYfw1BXDXcPWsgAl5mMKssT4OqTFnP5ySuwOyUZufE/HiGcrNnZi8npZlRKovVshoSgoVAZdnJD4bF8V9+feXV9aIhKg9u4CHONvRfaBA9GgRM5GgyXDcOh4p84oOXCI1WBkIKxuvnHpRe6kCvSIKQgU51o/TOpO30UwQLT3yx0A+fGMpCSwOTBcQTeFGm3x+DWJ3bgSTOw2wxSHBpZKQEeOeszPKmx7hWHqpPiSBx9ZDYdz9ncuGGFaFlOmhPExvJU8EXlxy91QL0tti1dQa5JB5/adBvOb6raTfHrWl2M4g02iY/AfMY0pnQwXxt45hUighqENXDbCY7uTcOJQ6n72XhsZV4838VmXhT+kLnjUhxEsP1UvID5Gcd7GNjU5FbrtkbKdt+TpNoI681tBcO8fPmZMcUWf7ICLRwnc1wbqZdH9M/lzMlj2rz8wvVF7ZoYDCf5/u5jLJFvB8P3PIQXmnseAC+WjSQou2YAJKBFrxrA7dC4+JR12B0GE884LW69gL+IcQOKTD+7SNyJunDDNH65cRoz1s5gsdfsEf7fjqP4564JlIVcTTvFuVWDn+dtxqVogER4JN7LBxDunRY/N6shoLR5hCHXeWJdFHaFhhMKMBq/YZGLhfLTCBw7JKqxZrfLST+pSXAvkpOHbzMXH7Wi/f5jggUDbdaMndRtd09xReLYUIprU3nCSMFGHIWVsTl64lmpCOy7a0xxVaI+bEXgO3EotqJqM7dNFJ65W+N/ZmE9vsg3Cl9rAYz3QYT1phDVdstGtadUNZjRU3uJe+F2hDdE9jMLGPX1dgrGDuTVv7/NBUOu4ReDZ/LCHbOwO22ocVZDuxbvSNjuy3+6sN1rZ6S2vxpd7egCRkCXBl+WrOaW5a/wl1WzWFaVXMrkjmC5a9rD93zTS79ho0HvwH6g7RAw4g8PVWFw+q9TGTR2ctzzjtDzSeU+rAi7qTdaRidIBJ9WD2RSagkzcpqHmNf0XcuRaWW8X1lAg26j9CcpbCnIg/UJlvq7IzHrOuZqy6gfuugdRDnUC26D+p8MxTG7BsfrNRDSwaHiG9Ob+5+aibG1kgd/dRc15eZ7mpalYY8TMWRXDdJdoRbaa0NjVN8yVu7sS2JVNSsIYSBldHxr4//xoiokcfs+cZ8L0kxulqmhDG5AbncRGJ3fvlskma0NI/bLNnrO/iMGYKv0EfY0P3BDI3rhmbMF30nDTIMVAbqBfVcN4YI4oZCNOza1524J66h1AbQ+rVL1tlUv0q6IszI5+ny7SIlSVg8OGzKyEvqut27miok3smfdnqaP5eU7/kfesF5xH98pa0oJTBgQk/fotT9dmJQ4jx/SN5LMLPHDytbBUY4hDW5Y9hLLqrbh10MI4OvStVxYcBxXDe+6uHyrJ98uze4At6LhVrtuSJZv98U9btgUzr/7kcQV9eqk2p+evZ14AqggOS17V8zxiWnl3FmwmPuHfs+LI77k8elzyM3zIeK4p5QxPhRdIaPQ1nLXouwwysQ6hMcww0pdCqEZmQR/nYNr1+6mYh9vW83kGUcwaYazKUXCiu/SCAZiv5K6obBkW8RXrJsLiNJ2l7F6Z8RfnVCsJTPGrWfqqEJsio4iDBRhcNYha+LkyJHgbKO3KQAl+rwEh0Q9pQr1mFpAEO6TTmhwdmzETCuCh/RKLkGxIBKZFB8jxYGe2nLOJlSQDS4bmbNW4F5ahGvFLtI+3YCe6uy439yQCH8YpboBtawePc3VZs6gWPvN6+mpjmY/f2s0vaUbpjVSouypJf3j9QTG9AGHSta4AaxetLmFwDdStqWMM649FYfbjtq4GE5A9jlHtBD4UyYMY9kT1zNiYC+SQQjB0388L+H5WbddnFQ70XxfsblJ4MH8xgb0MC9t+5ZSf9ctQrNEvj0czU9URcDlvdfhEl0j9FsDGfhb9eb9usr84DSy3G1kRVQSL11vclkaMDN/NUOctUSLnkByz6gB2NQBces2IgSMcVdy1eRFOFWtRRvkhky//Io0atelk2r4mlajKof4YkJEcSmET07DXlvVJKRfG8sJGxq/uusBXNkS6YRV33tYNd9DQ7D5x9gQtPHV+sFsLM0h9b0NZL20mMwXFhNa78VAJX4vXpDj8fHmNa/z17Pn8o9zP+f725/i/d++SE6Kly8fgtE7VpGmNGBDM1fz5oZRDqsnoRvn8DrEIQ3mCMZuIPoFUadUIxyRlcJVdtOrk+Fq1/8c7pue8DISMOwqhl2h/tSRbT4wtEwXRlYKTXludAOlNkDDEQPMydzVxbiX7cZeXItrU5npq49nWyLxVwTSbcfISkHvl5nc5urx2nTYInMLUa7JsI5aWk/a+2vIeH8NrhW743+UhsReF6DuJ+OQHgeENI44fAiPXf10wku/99jHhAyJFlnFG+qVxhaP0uLeP1+2hav/9Wby9wOMG9yHxY/9npnTJzUd65uTzrInrmdY/9wOtQXwben6JoGPRhEKCyu3dLi9ROy1u0YIMQB4EeiN+TE9JaX8lxDir8AVQHmk6K1Syo/29nr7nPRbIPghSDPPyfl5W7ALg38Xj0/obkmWGt3JgzvHcWWf9WTZg1RrLtZpMzhp8B1tV7SPQwT+12YRpwIo8Oqob1hi/JlP9iwmz+ngouEzSXP1xwhPhcqzid7eyPxd2gAJ6iAcqT/h7GkTmXrCKE65+almV2+FE6PCabqppcHsP73K9AtPxzemH8KTYDNwDYwCJ6KPn5NTdrPMmUOxvwZnRioTnzmDL2cvRKwMcvsdI5hyZi2nnOdD1xXeXTGSr9YMwb2sCOeeOsLZKRgpdkLDPZiO8tiLqYrOGeM3U5Bn9obqA3Yu++9P2V6RZXqafjKCs6bN4ycTXqC4NhUtBA+9PYF5y0dGWmjlm3HrqANC5n2NiLPBSON2h9F+8zYw0l1Ilx3hb7laWQrQ+qQTGJ1PaGBWc685kR88LSqGN5K90fA4yHxtGUogHAkYMj8014YytF6phIbmdU+4feseQiOGBGFG7oiGEAQ0MwVGSEfP9SAUBaXSZ64LibfyVgjCvdNQqxow0p0g4IpfTuPbP78dP4QX0P1a02uAhskFcUcgizZ0PCJGVRSumHEcV8w4rsN1W5Nqd6EKBV22HOUoCDy2theBdYSu8MlrwB+llMuEEGnAUiHE55FzD0kp7++Ca+w3FCUFI28+eB+GwGcoShrnDLuGn42dxie7V/Ds1q/Z5a9EIDCQuBQ7QSMcdw/Q1tiEpHdAI6fvUoSq0gtB72SG1O6zof7/4p5qUV2kQ/bLHGkfyZF9Ww41FftIjNxvwfcAhFaCbQik3YJQ80GGEFGjBSPYgKKq6HHym5w8qhCP2+DOK+dz9zWDaRiYj36EuzllbNMFIXRcKjnVFfz5ojn8c+dE/n7vf9n80DIISZjkQRvmxLaigW8eTmHOwylog1JBCZG5awnCMAgOzsZRVI2sD+IorkPLq6LPLzLZWN+v2ecrJbqhsKiwH5+vHcJ/5kwyxd18Q0CAP+zgoS+OIy/Dz2EDi7n45XOo9KaApkbFoUe9jQXtZC1UQJbZ2xX3RvvMiUi9KVhHSJCqQDps1E89JH7++HjEu56qEO6fiWtzecuimoFrdQmhYXmxdboCIcyRQqIHkpRIjylcTY8DKak7ayy2HVUo3mD8eQxFYGR7MNJcqBU+bA4b1eEw9ccPIXX+toQT2NEt6bkJUiZLyWfz1vCjY82UBeGwhrfah9/rZ85r85jwo/GMnDQsufvvBDP6TeCNHd/HiLwQcGzeiAS1Ok6X55MXQrwH/Bs4FvB2ROQP1nzyuxoqmb1rKTWhBo7tNZLhqfmc8819hBL0NM2lJZLf9V3Jz/oOxpH7eIevaXhfAu9drY66Ie8b0DeDkoNiG2yWNQw+2LUEvxHmpwMm4VA7vpvReXe9yJY9lS2O2W0qV5+4mEuONaOPVq3M4P9mjaH0x/ngiHIzBAyU4hBGHwe3sICzjtrDs1tHMusUFyIYtXKUxI/FwJBsnEU1LWKepSoI9U3He8IwaJx8bExfq+gYEgyZeLQ1qk8ZRw3ZySsLxhPWW2+B1Sz2ymF1iIGhhBouDdC/yAJ/En0mzSD9gzXYy7xIAcFheSi+IOF+GQRH55upkTu74Clit1IfJHPWiph5By3TbW4K3qp8yx1h9lHMe3vRPPHs0HSUknqMSLK6rBcXoWix+tX6e1R10RFND5gWROZ3ThtVQP37q1g/b2OzOZH/bQ6V13Y9SWZu5zcvaYvZu5fyz7XvYYtkMlSE4KEjfsm4rEEdamefbRoihCgAvgHGAn8ALgXqgCWYvf2YGUMhxJXAlQADBw48YseOxKFOBxtPbvyUZ7fNBSS2SAyeW9EY7Krjsvz1TEqrwJ77P4T90E61b2i7of4BMMrAOR1wgO8fpmtJZEL6ncwqTeXBDbNb1Eu3uXls4uUckpGHiCSgrwx6+a5sPbmKg8Jv3mXhWxvZucNF+ugx3HHPJWjArx+chaYZBMIaKU47+dlpPHrVUHoZlzf9HstCLm7edjSFgUyCumqGZTO9uQAAIABJREFU8wkBYcngikpemT6Xl//Tm9cfzEdvAOEE51AHdfUeHEVVxJN53eMARaDWx0lFoAjslw1Ge7EQwxAYqU68Uw9Bz0uNKduazBQ/6e4gRZVxfsDSXLFLvoY6ua5FiuToIkKYK2X1BRlQlSDyqvE3FtJJ+2Ijjl21TafC/TKoOzXiJlIAKVALK9GH5XZ++zvdwLW6GM/C5t+SVAX+w/rhnzgwvn2y8f+IRNqUrhH8rnxoaDoEwjh21+KZs7XpmxLduoxzzD82n4YjB7V02YR1XKv2kLJkJ8GCbJw7a+JuWAPgcNn5sOHVrrmHOHi1AMuqtuFQbByRPRi70nEHyz4ReSFEKjAXuEdK+bYQojdQgfm+3wX0kVJe3lYb3d2Tbwj7+HLZPQw05mEL2UnJuJCC8Zc27fZSHfLybdkGBqTkcHj24C65pi4NNtUVg1ZETsN1OIQXuyJxKwqk3YXiObtLrmPU3gf+lpNRUsL1hcexoL71JhXmZz7UWctwj4aq9uPD8iDjUsq50/M9DrtB0C/48KVc3ns2h/8n77zD7KrK/f9Zu506c6aXtEkvpIcQWugiLQqCFAsIWMArXkVBsYJeuepVsGDBqGC7olxEepOWhJKEBEhvk0wmM5lML2dO3W39/thnzsyZOTOZNBV+3+eZB7LrWvvs/a613vf7ft9QmeADj3yMZTPfy1Nrt9PY3sO8SdWcuWAKuqrSsP1MxkSacFyFt/dWIgWYRS6P7pvAzpYIatrl4qo6PrK4jh99ZzzP3ZtJkqL/owzPUpBtDon2/s/TNVR6z52BXVVI8Z/WZfV8cnqiCLo+sojbZj/J8tu8foqTy2mfl6EQDgvJSVMaiCb9bG3Kw7DoM06KRD2/HaEP3S3bNdzNYZQFvbivFYE9uEqLROlJInUVqWv4draitsVIHT8eN+xDiaUJrKlH7U0RXTbbU8yUGfqlINe/f4gzbpGyKP7DG54rSFNwgwY9l87zNPYHw3YIrdrjZShbDqnZVVjVEZSeJOaUUhhB7ndYSInW0otIWtiVBZ4LynFzFToPEXpdBwXP78yyuYa7yuCZvASSi8d7FcUyz9e3rYXQ63uzL+DBWvR/rb8+ZrP5o4FjbuSFEDrwBPCslPLuPPsnAk9IKUfU6zyWRv5zb9zHpaHfcXykjWAmASmZVNi5fTZlpy/nY6/9jJjTP1MMqj5+f8p/UBM6uj5MadeCGwV9NkIcfnDFTW+Ark8BXXhTwPyzkI6EwUXblo2QqSjRhcsC8wD/M3sNmibRDWjvDbJq23j279R47Ks6yz7cyoUfi1Iy/sOUTPoUxO6C1BOAS6d5Ik89toe1zwao/YeG7Wq488r51g+3cNK0/dkJqRBw3rj5+Zsq4IyvKay+yyKd9KobRS+chTUmAqpC+LntGHs7B2ui4RT46P7QQpZf83fufH8ZvVcupNMt6L/oMH32azb3XPUYezuKuev500hZAwzZYANaYqGe1I1UgW4NHJD1AeT+zO+nMEBXZwBSJgLhGVYhEF0JZNg3ZEaJ5Xjqm8PN3LMJS/RTEYfLSh1wTvC1vSi9KazxRaSne9W3kBKtKYrWFsMN+zwZ5DfqUWJmXiJq/OQa0nPHjDregBAovSkKn9jqZd8iEK5LclYVRkMXPVcsPKwVitKVoOihDZ4m0mFCagpuyOiXk1AzwXLLHdp34dU3QILaHqP3A3OxS0IUpBy+fNXZXHhhXnv6L8MxLf8nvGnwb4FtAw28EKJaStlXSPEDwOYjvdehImWb3LvzWdqjD3F6+ADTQz1ZAw8QCLjMnLWZ6x+6jVhlrjFPOGmufe0XvPieb3I06zoKbfSBHNduBWsN6DNRNK8soOumofOzYL+cPU5mAjf5mlkSMKkRUeplZJgPVWBJlTeccfx1a5wphVFqW4v59csnoKnedVMfU3jyha3c9N+vYqaXY+7/E4ZhAyYpC367v4Mnpy3AnqpQ8J8mE9e3sPfrrXztP2Zx/bdL6UjO5PPvedBra35VW6SEXk3nrsd2csfVE2iNhrCqI9nBKXFiDfr+HrBdhOvpu6AqxE/zKhdNKOpm4Vcm89juMMPzEz2mB7rEv7ibJ7Tx2BUKcnwa9mqZwSfPuZ06zjNlUGhBj84QeQOXfleHEOC4GLs70Bu6iJ/eX1lJFgWG/ga66rlGRnrH+vY5Dr7tLeiNPWgdcbo/fHx+g5kZFBInT+wfIFSvCHrhk1tR2+MIx0UKEG7/iip+/DhS88aApiJ6U4RW7kbpy6gdJk4gYmnU7iRuoQ837AcBBU9vQ4mmcp5kYPMBEKA3dGGNLxpG538YSInak8rNxzgESMCsKfaqXTV04/o0es+ahlVTDALUziThFbVo7V7eilVVQO97Z3qDAF7QWomnQVXoDSl84+GXKYwEWXrq8LUP/p1wNNg1pwJXA5uEEG9ntn0V+JAQYgHeM94L5JFTPDZImyZf++t9rCzbS0BxSMoxrOiu5EdCcFHJXr407q3su6ooklsnv8WN8XMZ/IHHnTSbuvcdchDkSOG6LnReDfYb/duUSvB9BJJDFkoHtQ+NygiFnQFpg/NGhF9OmYswbdyEilvkYnZkgpkadJx1HKazGn/AQbr9bJN7mhbwZM9EUhmphy7bT2LBWMo/3kz0t+3c8+QJBAt93DwKJdY1+2fwnVm1fOv3ddz4kQUI10VmUjncSICeyxfg39iE1hzFiQRILRiLUxLkM2evpjVZyMoDM3DzFuMGjztpozV2I69Q6A3Ck12eS07OSgICgUCZkgRNItt03K1h6JNgdgV0G5ls1mEeNIAj0WvbCa/aQ3paOQiBpjicPGUfq3ZNPPhDGAmaihv24dvXhasr6Pt7PIMJOQMMiuj3rUvQ9ndj15QQeHs/WlssRyOnD71nT8OaWtY/IBX6iS2bjdoe91YhcRMZHLDacVzCL9Vi7O1AqgrCcTHHFZFYNBa1O5lPGAIkhFbuoecDc72sX90r4O7lAojcV3TgS227+DcfOCzmpwQS88eQWjQWX10X2oEovcuOyxQN935IpyxEz/tmU/zAmyAheuFxOastaYCjq+hbm3GqCnGL/Nx1/3P//xh5KeUr5Lcg/xJOfGO8gyufvQurzHvpk1IDBGk0kPBERw2GcDi/pIGZgS4sUyHZIJlzoImdj4RxbQNzRjnuLBdldoKfbHuKOxd+iKqA9zFZtsMLb+1i9bZ9VBaFufjUOYwpLcR2HdZ21BK1kiwsnkhl4ND8d27XHZD+P7xpYTFeOGPgAS15DfzBICU4B/s8BF7WpgAUUIIuoqSHaatbuTy8lc5mlf97dhKPL63h8gv2ZH/tHkvjie6JQ7R80lLDuqQIeX8rSkEUOS8I+qlgvcrcs+OcfFo3ji14+ZFi9mwJIAE1DJeddyZfvnwdV36+AbUnxWAxYzfs8+qA9onjC4EqHH718hJ+s/IE0vbQ6Kih2ly5ZBMXnbINR8BjHZN4uHY69u4AosLyarTuCaBUmV7d176uVJuo5V04LxZDWkUkLdTuBLLQwAkFKA3HKQqm2NdRhOUM4LNrAhk2QEr0ph6mVHVy73VPoGsOV/z8Klp78wSED862zfujiVQuz17b14U9NpLry1dEVgPet6MtL+XQ8ms5Bj7bFyRatQ8nZnlGecD+wLoGz33mSITjrY6Nxh7U7uSQpCazppjE4vEeDbIjTvjFXcigjhMJoHYl0PZ14ZSHkQEdqQgvmSvjSkIVBNftw9jfw+FAAMGNTfgauui5eC5KZwz/xgMYjd6MPjWvOlNcRpCaXYWSHL7Smt4Wo2DVHtywwYHzZh1We/4VOOoUyiPB4frkf7r9af60d5X3j5xl5XBfj0tAcSjXU/x3+SvctHQqbkLx2BSZwFDsrCmYk8vwbW4gFIjx03tuY9KkCVz/w7+yr62bZNpCV1VUVXDL9Uv5VcdTmI6NRGJLlytrTuam6efndfVI6SKTT0FiOdidQOsh93k0aDYDfGPviWxKlA7zHAa2aeiKIJA2eWrO4/iDEinh7i+O59ovHaC0yittuD0e4Ybas/IKtoWEibpsH13fOQ51nskXZl7AFYFPIKV3LZlJvjTTCrEeldrOCG8//lEWn/gb7vjqcdgNaZyIHxnQMccVkZ5dhdRVj82iiEH9yf87K8Ll19c+wozqdvx6Jg5jq7wRq+CWDafjvlzsnedzUM/tHMKgkQ7I2gDu5kD2FiVdrdx5zQrmLYxiu1591bufPYXH3u6f1YmESckf12GWB3ngxQ1UFCdQFHhywzS+++QZuf5/y8G3tZn0cVXeu6cqDOcawXIoeGEnRn0XUhV0X7kQt8CfZceoB3pwKgqGJv5IibGtheD6BtREvxGTQOzUiZizq/PfD2+Q/Mp5L/HtR89E6l67teYohY9tHhIfyYfU1DLPZTUoDlH41Fb05t5hFYSc0iCuX0dri+UWGD9MSMApCqAkTYTpZNvuagrpmZUkTp2EUduG2pn0lFcHu8Fcl+AbDQTe3u9lJQd1/rz5x1RNHJ0swrHGSD75d7yswb07n+s38JA7ixnWsCkkXZ196TDXPnAqbsLzuwlAuBLhuIRf3g22S3reOGLBMJ8/93Z++8ir7G3pIpn2PhTLcUiZFt+ve5guM07cSZNwTEzX5qF9q3m1bUfeu8vuWyF6C9jbOVYG3nIFn9h5NlsSJRyOgQdIKhrXXTCbzlYNRYGbf9jAMw8Uk0wo2K5gnL93mMIlEn/aIjW7CiIKCNjR+ktAeoQVBVQNNB2CYZeKsRaLZndywWXLeXj/bOxGr2CJ1pNCb+4l+GYjRX99C//b+9GEnac/+ft38tQGplZ2ZA08QEBzWBxsY1ZDqv/sAjtv4FSoQKnlqUBmiop/5+a1zF/QjU93CPkswn6LWy94leNr9g840XsG0+alKAhbWffzRfN3cdtFK6kojJHhLOLL0PgKH93EmPZ9+Ha0Ely1G+VAtN/P77pgORh72tHru5CaQuq4Sty+0ngZZUqnahi5BFd6wcaElTPJTh5X6Rn4EbJ0gz6L98zfy7JFuwDwbW+h8MmtQ2br/cjNe8ibbaqr3oqMXIbVwMendSQw9vcMMfAyz/GjgQDPjZR2cgYnxXbxb2tG9KbwbWtBP9CTX2fHkWhNPdlrKQmLB77798NoyT8f73gj//u6lUdwtkBfGSOfFI0UAkNpQb2wA+dTAbqXj+cPxnOknUFc7SIbmUcCN+lYPNywduh1ra2QfpqDa9cePtZEK3nflotot/1eVaXDhQs9DSr33j4G8Iyzbkiu+87xvNZbhV+6nBusH6LlYwiX6MOSxCk1KBVe4O6copFTyP2KS83UBN3t2pCvWLgSJWUTWtdAQdDylvEHka4VwmXhhCZCvty2tccCfP/J06itr6DPIsqEmrekoHSBWP8qpbKwl3kTWjCM3GN9us3Vp2TCUbaLb1c7INB9ckjOz7L5O3nic3/ki3MfJRjfTnBXA+bEEqKXzady+x5Cr+zxqnCVDyhXJ0Ft7cW/tQVrXITes6eROHkSQyy6qgyr9uivbc8e3dek5JKaQcZ9UL80iw8u3kzAsLli8SZIWgRfq8tOiPJD9Ot86mp+yiZgl4QGnDF6HAkFYvD6rw9SEfhq29GbomjNvZ688yCdHaOhG601lnPe41v3YFrDu3f+XfCOlxoenBJ8qHCrdJIfLQEBxqoY6t4Mm0CRiHEmQutbWgukH5T3dOI+N4CJo8phpxZxO09BC3MtA/VijjZ2JSN8ue7kbCD0YJASZKMO1Va/Pxog5WL8I4qbhjXPRbKbTVOhYWk1X6qrQd+TJPSVfSz9Qz0bQ9VEHYOwa9L1agHpcCViSgIRdAkImwojj+bLYCgwtbSTPQyTkauD8+daSjoS4EqcogDx06d4BcMHf74S2nrDpEwVv+E971ha5+rlH6QzHsAZqDuU0JAdOpRauS4bF9zdgew/S8NJLEfNWRmAt7KvjMTAtFF70wTWewNa3UsuchATZ83zBXzr+ok4tsCPlxuoGEmPeigkqZkVHrVxoG6NKnDGRIh+YN7Bn6HESxrqC7wqgtCrdYi0jVVTjEjbaM29OKqAQQbYr9u4UmCoDqajcsaMvXzi9PUABAKOZ/xGOY2WgLAdb1acZ+BR4gcp9jICjh7XLXM9yyW4dl/2ugXP7SA9rZz0DM8V49/eilHblntfAd3TSvn8V3/P975yJUIICooPnoD3r8A73sgfKdLXlWVfXPMDxfge6sL/505QwVkYyDlWCMAPBCxIesZfdOsIZei771d03lvd/1E+VL+aHdEmrq62GXfsusOfW6eRHpZhMgBSoj/Xg+8PnYguh9R1ZVjLIl5HNNBX9OL/tad/oqhe71wXXqmuwR3rGWFrcgDrVxMoeb2YJXsDrK9J0+BXwQfKST0oZRYgqTTi1Piio2r/Fafv4jmGqdJjCLSOeHaM1LqSFD65le5L5+EWe7+VIiSuFEgEz+yYwn+cvYa+E57cMJ3elC/XwGfgri1EndmNnOR4ViThqWwOnMnvaStGU4ZOKkxTsP7VCAUv7EJv6Mq6A+yk4Ns/XcS3v/AGmuripCS3f2xSZnYvskZDb4uj7Wmn5kyVTU0lo5PztV3U3hRuQPekEDJQ22IUPrkVa4JHU9QbukhPLaPro4s9lUoNSDkUP7sZ0ZtGFvTnaqQtjd9e93dipsGU8k4qIx6lUEqoCkc55327WLvq4CY264KRENjYRHL+2CE++eD6f49yefliAkKCf2ebVwBmmHPSE0vQOpOskZ1cVubleBoBg+8+8zXmnfbvxbp5xxv5MiNMuxk7+IHDYWCARRWkLy9Gey1O6oYy0PMbS/XsbrQXqtBQ8Bs6100+iV82PIvtOji4BFSDKeFK3jfueLZ0N3D96nszgmXwjwMWz8wRGHncA0eCPrdAbW8kSzscFq7Ef1czxkux7AsevL8d94EO3HINtdNBxD1jphsuZ17SjZTw2p4yNszKTYu3ig2u/cZllIVmk3JM6qItfHLNcsyMYVWQ/Gray8M9yhzYluBLl033Bs1BfHrpE5CSiMGLIMclsLEpw0fHo1CWmKiLeon5Xf6zbil31qyhUDV5c++Y3KDnQKTBt7wbTIvEmZPwUlyF5xpyXdBUUnGFe59ewKfPXY8/6D1w2xYkehUe+VYAo82bmUtD4JZrKC0OKw/M4Mr7anj/ou3s+V06a+AHI/zKHlaoUwgXpOnMV3RkgFvFt6mJ4BteOTrhSsyJJcTOmAIIQq/XoVgOvt2ezpAUXsARTQFN8ZyEAZWuc2cTfL2O+Lkz+mmTCO59+QTuuvIZfLqdc2t/QPL1ZRu59cWZ7HjCYGAoJq+hzPw3sL4RkbJILJno1bC1HQJr92Xbl/0ZI37ip07Cqo4gbAffthaC6xqOKPlpNDjUVUHfz2c0dmM0diODRrb/ZtLki2fczt97/kC4IDDyhf6JeMcb+TvmXsFN6+87ehfUBL03zkBMSSPy+M2FAKlCyRkmt025lJOOq0FXVU4ZP5VHGt+gMx1nacUMzq6cg6aofGLNr7IGHiDh6ny57iTunvzaUdeB2rg6wI59VYip6bxaK33wLW/NMfB9UFISccDKxCgkuiGpqklzzmWdfO8zE3js6kUQGGBshMMZxWmKAjP55oa/8uyBjUgkRWqSu8e/wSyjB0d7H4WhcyE9MqNWSvjRLePoau43wtInkKpAWBLrhBD6m3FI5H70QoLalQAJwTV1JN4zDvXknqzraUuqlIu3XsCEZIr2ugpAgiMJvL0f/5ZmhOVgjYkQP3EC/u2tSCFInKaC1k9BxHTR2uPoDV28uDXEiZMqqa5OoiqS12on8MDjY0i47QjhIMMK6StLMC8shKdV1N0xmprKuLf5ZApf3YTG0OcuAJF2MDf0eAlKF5Yhh4jyew/J2NNBaO2+HKE2Y28XIbGH1Jwq9JbcCY+Q3v50H4Mm0yfXp2FXFOTy/qVk7dYqPv37Zfzm44+iDFqfGn7JFTe2cseWKaiNplc3IDGY6Dq0b4EtLfi3tCD9nq78YFaOG9Tp+cA8pO6VOZSaQmpuNU5RgMLn8pMX/pUQ0nPxAMie1JD+f/P93+Xul779z2/YMHjHG/kl5VNR8GR+jwakEFDk4vYqHl88zxssBLT7Ozltbn+t0onhCj4/86Kc4zZ01eHIND+a9DqLwu1IAWuiFRRpnj7lkanRD23T3BOTBFdrJCeZSEXmH0SiNr4nosN/mKoA20VRJZap0LArwC2Xetm2wd3NOF8sx6wwMITNjeO6+OD4uTxZ+w1WtNhINC4r3cUt4zYMuOBDWDHQg6dhm6sQEjY3VrJ693jCfpPz5tRSGk4Q7VJZ+Wi/718WKqS/Pwa3w8WZ4gMH9OuGVtKSisAuL0CJpfFvaSX8HodOJTdHQaiCfYEAjtBBQvilXRh7u7KCVPq+LiIHophjI/jquwit2E38jKn9Il26ijAdfG/up/v4cdz84IU4QvNYN0jUizoRHywES3pfVObBKwvTyMYQfSG/1PRywq1DV50SSM+sJLnEWyXp21sxM9ztLFwXY1e7518fFHQWjouvroNEHvExCUhdIfh6Hb7trQjbxRobIb6khvTsqqH+cr+GVBRSlk5YzS1ooShQXZwk/u0JKDETpT5N8AfNMIrYowBEKn+xneTsqn6JgT5oKtb4IpxCH2p0dP774QjTh5WGMMx5o+F1bVqx7TDuduzwjjfyACvPvp3zV3yPmJM66LEHE8UTCogJB3+pJLC7t4UpBZXDHtPQu53X5j+afRGEgNMjzdn/P9pISI358xt5dcVk1KXdSP8gQy8lal06kx6evwHSEJAWuI5A1VWUDP+vekoll37mQhZ+8HiEG6Mg8VVU+y2Ir+S8sOCCubArUcDMYHRI3zQNejv3sb3wAT7/m6exmv1IW0FXHX7x4hK+dMkK1v3EJTp/IuaEYpSkhW/LAcQEHbum/xW1zgijr4pl5YklIFWPThjKsD6SLyThnDyJaI5ABG2CT9Vj1HXmuAEEgOXg+rxh11/bjpCS+JIajIYupBCY44rouXIh4RW1BNY3gvAUJOOnTwZ/ZlanCk/bRgARG3eM7mmZZ4yXObsaubrek2boe94AqkLipAmge301p1dQ+OhGYmdMBSFwiwKgCdSO+BADn/OcuxJDDZOmoMTSGPu6solQRmM3hd2dfOhek8d3zmVHc4ZIkPnh9rYVo6lDyQGWCW/viuC0BZDTwR2nI3+lIjqG0hwP5fW2y8OZAXMQHIlTHMwx8l6OhITB7rwRrn+4n1o+/v7AbY5fA0WgJK0hq5M/fuchrv76Bw/zzkcX73gKJYBhGLx47jdZe/5/s/q87zAxMHIprqOV//Vi86YR959vfKEvMTNr+EZROGhEpNNwoF7P2wcFSe8YF1Fq4rxY4mVzZqjWSE+r+q4T1wz70ksB9Lr4zirj5uU3cNNPP853n/4aT8T/xEkPL+NbE17ikpU/5GOv/5iHmroBB02AoUg0IZkVyh9cFQJCoXqefrWF9IEArq0iEZiORtrW+a+/n81LY08jOX8sTnkYa0IxsffMwLc2jdqkYb9UhP10KbGTp5O4qhq3SEXqCtaECNEPTSe8ag9GvecPFzGJzEdeUiWyV8O3sz2vn1cAajTtDRyagjmxlKK/bcA1NMwZFVDgo/DZ7eitnrtFSND39xB5eBP0SNxWHeeZUpzXIjivRHD+UQL1Q+WRu649Aau6IMv3NsdF6PzIoqyB72uMNbYYtzSMWxLyptCuQOtM5OWVA+BIgq/Web8jHu1fKpCcVuadNzDTVYJrgvVmN7+57hHOn7Mz51Jx0+D+VYtImP1tsh1IOj7+/PuZsNWApIp0BMn/rPTcakr20ocMrSORnxKrCE+zZtC2nkvm4frUnHsNR488mui7vutTsQv9nqZNygZVwR0ULP/THQ9yafl1PHzPk8e4VQfHu2ImPxCKUPjDqTdx+vN3MHjslRLcbQGUSUmk/8iMrYoyonCZlCkUnKP25kkJPR0Kv71zDB0tOrfftxefv/81dyR02H62pkpQp8a8bybD5+5rpovkWf8k5p3cxcbXc4W8+tgQyi+m8ourv0hNyBsoTdfm42vuZUtPf+HvbsfP8pbZPNY5ifunv0CBlhuky4ft8WKeXrcNnHw8boEpjNx6plUOnf4KeNOfPUe2GqRCNVj3FiIKHbBcfI+3oR+IApLJ81MUnGnwqiOxhfAKiQPSBrYCCYYV7JSAUxLELdcx318AsySJc8cgd2kUPLsdrbkXYeUKRAgJpGxCtzQSO2smhAe0PymxN5UQ2lCLffb0/r6pKr0XHIdvewtqNOUlBWm5zBMAt8CH2hYjsKEJJZrCGlPIcRPaqG0y6OOi57QF0GIDBhQJToHhGfc8UgZmWqF2U4CAYXPbspW8sG1KvzwD8NtVx1PXFmGWtg9fLIFTGuLB2sV0yDS+jS2klGrERAtzjIHzuRDGY53oDVGUuHXIr7xR30FqbnXuMtt20JujnkzCAEgg8sgmr8j4Id7ncJBvVWJVFWI0dPdPFjJxDdenoqQdb5B1Jb0dMX75ud+x/JY/8kz6L/+E1ubHu87IA/g1g9vHfJjvN/6BlJJ5caXAbTAQpTYchfKJmqJwTtUIxT7k0Sn2Df0rj0DYJdqlsv7lQh74SQXX3NqSlSBvNYPcvPs0QCAKJNrieB7XlODp7om89Oe3+PltY3jhoRJcx7vu2C/42HLKdH6y+FoOJLu4a+vjRDRBS7KOLdGhTldbqjSaYc7dfDFBYbGstJ7rKrcQ0ewhxJCEo/K7thlYfhOPgzoILpmi3JlWVqYRx0dxnysdNCgIbwm/sgj1pG6Ez8H3SBeTZyf51u/qKCyxMfwSKddxx+YTeS45HmyBuzuA3GmgtsVwDQ0lZec1EP62dpL3jkcJKDiAjAkK/3c7IjX8/FQAWlOKyIObiH5grid81bdHUQldXM2y4zYRNf386CgxAAAgAElEQVS8vH0SyZTmaZmv3uuxXjKXVroSnhJiawwQ2OV+Qq95yotCgtYR50BYRTMktjk6GqPaayJ9Q+r0AKD7XCbPzhhQCdMr29nSNMD1aDq8uHkyL7qTQFEwnmvHt30fhk9Db+xGxEycHWHs0iBWWRnW8YUU792Q914jITW5lPiZA5RZMxINxs42wq/vzTlW4rGJ+ozr4fraRwupKvSeMQWtI05gQxMCj6lk7O8ZshoULpDJzh3cJsdy+M9TvspPX/vvY9ja4fGuNPIAEwvLuLy7mfedvIkmM8TtvzuH7hNs8LvZGd7hwqdofGLK2UwKD69bIZQwMVMjqNtH7H/vO9/nh6/8sp4PLyzg0fvKWXBqjAVL4yQclQ9sO5+s9y2uQMgddqWx1yrglh818oW7GrHSAtdQuHv/AtZ3Wty49tf9GYsy9/55WgZAQhr8rX0KD7VP4cqyndwwZhsaLpoiSTgq62MVrIqORalJ47b6wBl0QdPB2N2OOcsr+qHMj4GpMETSt++ejsB5tYg5u9dw8mXNXHNLC/7ggPiDkHx77mpaf1/B+vqxAGj7Oyl8dvuwflwBJD9YgqVp2X75/rcT0sMb+JynYDkEV++l94J+jrSqunz09E1cdvxWbFfhyxeu4rN/uJDG/93vGe6uJL7adszxRUQe3eSl3GdaprXmKjkKV5KKq4yfa1G30Rjik+5DUZnFZTe28dj9ZbTuN9Da8k02PObUsms8GqOqSHpTmaIefeJvishZYZiTSxGWS/iVPUggsK0FtrUAHv3RzCRaHcqr7moK8bOm5a7gAGzHM6R5XDgDDTyactDM50OFVAW4ErfAT/ykGqxJpVgTS1CSFv6dbbgBHaV3mNjfCK/KttW7jmo7DwXvWiN/XE0lf3u+mPH+OBMCca64cBO/7p55xFGID44/iQ9NPJXxodIRjzsQb+aq9RfyzJInMAYl0ByRm0iFJedEeeWpCFXTLf7ePom/t0+ir2PSBmdTAepJnn9cxaXCSJJ2VJZGmnhvUT1TAp4Gh6KALyBJuxJXSm4d+ya7UhEe75iEC4RViz7XQNzN8MaHgZO5/wPtM1kfr2RZyV5CisVLPeN4NVqNRCAqTBiXgn0+j5GRGUUKntuB3tJLXEJ6dqUXyHQY2cFrS4Izirjha2/nLwcqBcctreetmiCkBL4tB/K6OAZusxcGQe8/QtuRGpUIV9+1tObenG2aIjlxciM+3cGXyRu4+yPPcukjp2O87RnI0Mrd+EoCiEGFK/I9accR1G0wPKE2y8nzfCSOA++/to1l13Rw62VTqN3UX5BdKN4s+bgT4nz2u/sprbSxHUFjZyE9D+xHn+4iHBersgBZMGjFpanYpaG8s2e1J0Vg4/BSwBI8jvyA2a9UBNH3zR5a8B1AV0lPLcO3J5dLP/BIuyJMct4YCl6qzfhh5ZBjZJ7zRoIEOq9ZAsZQrZ3kovH4d7ahdsQxxxdj1OcWsJECXL+OOoKK5b8K71ojL4TgE++dmM2q1gst1LibNUaHiqnhSr6z4Comh4dn0wzEvav+m6Qa5IxNF3NT9WYuLq0jpA51ZRwqFAUCIYezro9yY9s5dFp+TNRscNXdFEa2+iCqcOHE3Xx+7EZ04eJXMkvJAffv+zYcCV+f8GZ2+ycrNnHJ9veRdDWcwyB67kwWc/f+YgYvqIUAbUEMfeMBxFYFYdoYdZ3Zsn7BdQ2kj/Oer9BAjE8h9/nzz+g1lf3RyNDteH26te5U1sfLUYq9a6e/UIacoRP4ba6Ec45h7bRhXL+kglOlo7SO3u2Wo9OiulRP7GRKRa67RFcdZi5KsHsDWSOhd45C8qGvjRKE6WQDt7lPRpCMqXz745M4+bwon7y9iS9/cGr2OOkKrri9m49e34hpKyTSGu2xIA/+shxtb5TCvd7EoOO6E4fcV2/opuC57fnbxPDjsQTip9SgtSXw7+rPIE3NqMApCeaf8UiZpbcO55JxIwGs8UV0X7UQY1cbSsJC7UqgN3t9EI7Mror6W3kQCIauKvrul9HSV0wHN2TgBnSE6aDYLlJTPE19e3i5kkhZwbD7jjXetUYeoHrsh3Fbf4kQMDXQg09xSLiHZuTPqpjN9xd95JDvXWumwfC0LJY3z+GD5XuO2MCD98rOOSnOa8dPpa0rkB20hMjErSakkPsCfNTZyyfGv4U/Txp+H4Tw5v8BkZsP8FzPRBQk1hG/Hvk77Hu+HbV9qPEUSQsciUwIREiizIvh2AL2+4Zey3KYO6YZV+bnLn+8aistDcdTl8oMBH4Fc1kE35PdKM399x5oRHwPdZGY7ge/90zTV5Wg7WjKUjbBG2/yze6lgOR8T8gN1UVZEKNlnEurGcjV7ZEQDveglyjYXTKTOToMnXXQHikgNbea1JxqpOH5xoNr6nMYPLYlWL+ikM1rQ/gCElVzsW0le60Hv1XEUz8rYNpZku4OlcWzW0jsSuMFqry7qV1xnPKCft66lIRW7R6RvpmvB32Pyb+lZcgokJ5RkZ82CeC4+LaPrM6qNfd49NKwj9TCfqEQEUsTXFuPf1f7CGcPAwlaay92VeHQ+7X352gEtjRjji/CLgmiJLxSgnpTD4o1/PNZvvGHh96eo4R3BYVyOAi1EqF5OignFjRTrifRhlF/VHBRBu3zqzqfnHbOId/X7fkBC6s70DJL9MJBSSUHQz56ZB8VMhWHcy7tZkXPmCGrEqGAKLZBlVxz8tsjGvjsOXkonZsTpXk14scZMXzC5vCIcv1QovlnPDKog6og3w57szkFtMW9UGWSk0fvuGi2zY0f2URTNExnt5bzzISA2cFOfj3tJUq0Af5TCfb8fveFNAC/8Gq3Avq6BME/tmXYKBJnQZDEzZW4xSpSF0hDIANDzZkE7NJQRhNeopzQizIuja64bE6U5BwrbIfa37moCQddl0ybnwC8coaDn2rfDLlve/z0KSQWT8At8CN9GuakEnounY8b0AedBemkSrRL9QZJco1wrEPlrYc06l6CxlofG1/PnWWGVu3xpBzcTFlJ00aJmThhH7EzptD14UV0f2Au6Ukjuyz7aI1qTwo1evAcFsDL6t3d7pV6ZLjhzwsq+7a3etzOPrjesr2PTpvbikG3Gaa9wVf25CpQujIbbxkIo6Gb4IYm/Lva8dV1oqSHn8X/tf0+SqpKht1/rPGuNvIAovDLgB9VwPVVW1hS0Jwx5gN/ZklAcfhE5WYK0ilIu4wVZdy75JNMLag6pPu5rgvJ33JVRS16xsh22n7Sh7CCEP0TqJy/H35+DIGM0J06jLNYAH5dJeQ7tIElpw91JvogpcyzIw3MCHRiyUyptiOAuSwy5COTmkLiBC9jU3b40LsFhue4R13cg5iRAL8Ntk2p2cL3rn+KpxumctmPrkL3iyEDlSJAEy7vL63r36gJjy8vQAYE6YuL6f1VDdbSMNIn0AKS87S9XBnbnZ0M2KcX0PvHSSR+N4HkN6sQCTnUQKiC2HtneI9lTBql0nv2jhSEhYUrIW0ppJKC73+mhkRUI51UsdIK9dsDTLrMxRmrDftUBeAEDdJTy3OFvhQFqQmSc/okCwa1LCPUNhyEAm+8EMFM9/+mTqGf3vNneRr0XUmUnhRacy9uQKfnsnmkp5fjFvhxKgqInTWVxIKxw15/YPsHw7ejNdeY9h2bMAm/vHtEF1AfQq/X4d/agkjbHuWyvovIwxuPqMiI3pGg8JltaE09iLiJ3tBF5LHN6HkylUeDuafNoqTkX+eqgXe5uwZA+E5Chj8FsXuZHezlzn2VTPV3UWmkWN1bhS0V5gQ7+M/qDXSukIjPBLn4ziv56hcvPbwC3m4j4DLGl+AXU1fyPw0L2Z4s5t6m2dw8bsMhCZP1uWCkhHRC4cZvNaNmvvELS/byt/apmLL/o1dxmUiMT1xzHYr4+aG3PYMbZm4n1etH06BINXklWsXrvdUkXY3Rz+IH5yj0m5vUx8tQ6k209V6tWDeokzhhPOb0ChASMTOGVQyQUfpUQZ2RhBme2yMBlFWm+epPlqBqgrAvf7DLr7hM83fnbJt5o8tbn56SrQAGkPxyNUngPUX7iIhCfrdzJm4b+ApNHC2zstqQInBPq2d8BJ7xFB6fPXbmVK9CExIl7GT6Cymp8oum2ZyTiNDbqLPqPySd+3NllC1TsC9chLNAoDb2DJs275QEveLbg33GmpqRWs7vvR7pDVYUidBEjiyBU+AjsKEJN6gTXN+Y9Y3HT5mY0ZYZcH9dJbloHIHNB0Z05eRrh397C9bEYo9zXt/lGX0BStQrGCM1BbvQn00Ay3tNCaHX9xJ6fe+I9x6I0Xjo9aYohU1bSM4fQ3BD06ivPRiaofKVP3/usM8/WnjXG3kAJXwTMnA54801zGx8k429KrUpydmRBi4s2Ysq4NHvFfP6w2Xc9cJXmb909FKhjnTpSjUTMf+Mar8JyvjsvlnBLu6f8SK2FPR5RfckC6k24vgUZ1Q++j53SiCc+xF9qmorm+Kl7E5FcKRAE5ISLcVPp62gVF8x6vbnQ01VkrurXkcCL3WP5fmecRkDD8N/Hv3GX0Ui0zCvuI096Qi9jkFAtXE7XKxmF3eSj8S3xiCaLLRNCdT1SYINbRhmmuTNAUR45AdjofLVbadgWwJXU4mmfBQFh0pRJB2VrYkSMoVuCXyzkZ1pF3441Ee1INRKXSrCy8mxUO6JaFmWwPhTO/6/9yDM3MEtsWisV5LQr/dfSwXKzAFsH8H2dCnbW0oBSbC4EX1/rttCSkFM0zGvjWA804O0+5/wQLOt9qY8et9gOK4n0HYYqyvHEdi2yLmfsb8HmcdVIpLWUGVMyOr6D/RZjwZCQsHT25E+1WMWDaRGAonF4zEnllD0l7eOKh/+UK7j23n4VdtKxxTz260/JlQYPPjBxxjH3MgLIc4HfoL3CfxGSvm9Y33PvO1QKyHwfu49+SLu3Pwwzx3YyAs9NaxtmMLEv1osnjid329cRsX4kSURBuKRhjd4fO8f+dXUZxCAJQVCrGdbvJigajEl4C3xtD7XivFeplbfg5RpzOYluHYSVR1ib0aFgOrw62kvsyFeSm0qwlgjzpKClryMtENFVoIBWBkdQ9LNJ8/rfXoKLi4KCg7fqVnNGUXNKMDvWqbz+5bjssVLkq6Or8RG3SXx/9cBrJNCkJbIJj+xOVP4zNUrKGEnPwydijUKRo9AeJWbENzz8ol87r2vEVLtbP9dCS6CFXVVGI934ftLB5UVJnfcX8fnZDkdToCBn/w0fw+Pd07Czsh3CgEYAvOqUvxPRGGAkZe6QBbqyMBAWqmEsjSKaZJP6llqAnNpAfrmob5pe5ofgio935uG/74ejD2dSFXBnFSCvrcd1XZQYinU7jhOcThXVMyVBDYdYLiZ/IiQ/fyTgZ7rfFcJbGhCWA6JUyfnbPdvPoCaMfCjbcHA+4lBvuw+N03grf2kp5XT/b7jKHp86yg7dHTQ1z4lefgJjadcvOTfwsDDMTbyQggV+DlwLtAIvCGEeExK+c/91QZAU1Run3c5t8+7vH/jFYd+nb/tW8ODu3/P3ZNfBTyjoGeM+ZxQFzFHxZGDaMDWGlxzPUL2srztMqLRTdw25dCzBD0IhJAsCHewINxx8MMPE37h4Gl85houFUmVEafLNnBdwfVFO1ha0Jrt78PtU4dUp0pLDf+JEG2chxK1vIBhjQJIIuMEFy1q46ebHKw8RT0G44vT1nGrfxnugh6eqK7g+S3LuLF6MxeV1ONXHDbFS1j+1nQ6v9FNYJcJSL7/4G6qxpvo210Gm6PtiaL81bQciT3Lj74ukd0kFIF9AygHYri7gxi6TfncdloCCurOFE5Vn/JkLuypIaTaAU4uJ954LkpyXBCnqZjEdUGSehVui4H/iUbUpJ3V0I88tpXY6VMwMwFPpTdNeOXurL6LUFxkNvYz1OTmc1WMxvcNIFyJf1sLyUXjM4MbGDtaCb7VOOzgkM/oj3oosh2K/m8DybnVJBaOJfjW/mOa3dqHge07kvu99/rTjkJrjg6O9Ux+CVArpdwDIIT4C3AxnpLIOxaxdBs15s3cP6MTnxgqRywEhFVnyHYpexCdVyOFn0+UJXhaTuC+5plcX7U9e97Bs0wBBBQ/hNXzI3p61lMaTh4TVUuA95Xu5dmuCaQGVZvyKQ6Lwy080TmJcj3JJVW7MQbUum238xdNSEvVE3QK52pLXDR/G5qAp+Y8QcLVeLh9Mr9unk3OpyY9vuQpBU3MK+yg4KJWeoWBEN4A8pOmBfykaUH/8QUSfiAxnuxh0Vv1FJfbqFrfs801Ny1WcMg2APwqmAJXzwQnNYX47VWIQg1RmEKZkcIQNmeW1PG3R8YgI8MvzRy7iM6rK1DbYxS8WIua8AK0vhd7SS2pQj0rwwpRQJvoaeQ79T4SJ0/EGluEsF0if9tA+OVaj5dt5mrpVE8wac34/MuqLZr3Gdn+jGTIR/3quKC1RLHGFoEQBNftyxU+GwGHkpgkwGM4ORahTHGUfxaO1mf02RO+zhd+fQMXfPw9R+mKh49jza4ZCwys89WY2faORm3Tp5kd7MSv5Nebh/zfuZc7aoOM4VNczitroMvxc8OuM9gUL6Hd8rG2t4KnO/v9+n1GX0qPIfbnH5ez6c1LUHxzWf7ybJ7cOO3od3AA5oQ6ubZyG7pwMpRQj9SnC4fnuydwXvE+fj5xBX4td2k7xsjvow0rVvYafX9fumAFvkyA06e4FGsmH63YyQ9qXkFKmQ0+q9LlhxNXccu4DVy27UJiij7y4CYEGArmBRHcBYHss5wR7B5yqDco5aHaCYieNpveZccRff9xdP9gBu683GzQlNT4a8d07JPCONN9+TmwLshmH/g0nDERej68kDM/nebnz+7gvk074RQvwCz6xghDYJ8QInrTTKwJxaCryICOG9QRjkQZZOABzv9wJ/e/vo1fPr+TUKGT0x8nZJCJFQ/tI0MHgbwUQykpeHYHRQ9toPhP61BjI0tyC8ApULDmBkA/dAM6eCLwTsPdn/zVv7oJwL9B4FUI8SngUwATJgwtevDvBilNZvo2D5EqOBwEVIcry3dx+bYL+FTt2d42xeLOiWtyjnNs2LfLx91fGM/ODSF8P9vPL1bczHUnPYtPO3JtnIPhyvJapga6ua3uVLI8bFfj+zWvMSfQxX2rFnH9aW9iaP00jc9Ub+L2+hMGJVRJYq7KDeeu4fVtNZSEknz67LXZrNCB/fApLkuLWlheuhJVgX2dRew6UMrSRa18ac/JJFyVUZsNQ7ClshJd3wzAVeW1vBqtxhrATHKHme8IQIxP40zQUCakUCPD0fOERwbqozgO0FqQNsi9fkj2F+eWqsqWijncNmc7K7rGoCBxB/cnoCAmWsiOUHZTekYlatdelDxslg2vhVn3kpcI5Q7SB3Iqwqj1ncNO6e2gjpaw+vs8fC8Hcd6Hd8BIAYnvjSX8+QbEMNn+I7lv8koXHRHyZSK8+3Gsjfx+YPyAf4/LbMtCSrkcWA6wePHiI8uy+WdAmiijFTQZBcKqhUAiEQQUi4Whdk4qaM7uFwJUDaprTI47Ic7ODSHMpIlfeY6gMTQwNDp3z+jRaRnc0zSP57om5CRfpaTKd7csoWtlJSlb5fITNuPTbDRVsuLRCPffWUigsQ5/qUrqo6VY50UAAZbAmWhy3ymPjOr+88Z7qfCzx7Zx/lxP5GlNb2Xe4OawEJCYHGTNykJOOjPK/FA7F5Xs5ZnOGlJS9QK4rkDR5FBeuQB1XiLvZUe+p4Coixs3kPuCyGZjyCG7WkpJ2yp+zcGv2yRkvgB3bnvSMysw6trRm6IImetBXv/y0EzN7FXM/EFECdhlQbT24amKI8EfdDHTAjePhLQzL4BbpsEI8cth76kM1eI/cggU1WXRGVHWvZhfEuNQ8P7PnEdzfRtrn3jz4Af/C3Gs3TVvANOEEJOEEAZwFfDYsbqZG38At/U03Ob5uO1X4Nq7s/ukdJDpV5GJvyGtw1eEE0qYqJOn8tBhwpWC84vrOSvSyDcmrOMHk1/Ny1TzByVX39KCqknmnBilpDL/1OhIi5IMxs5kMSvzZNeCwApDutLGcRU+ft+lvFU/hpceK+KuL0ygtdHwGAodDoF729Cf9mh5Uld4qWd0Hru+vvT9KZmYhSGGW0UNM/gKgazUuaPqDFKKihBwbcV2zo7sQ+704zxdhvN8CW5czfqYpZ3f63JI6LVx1xZ6bpp8HHZF8uK2ybyyejJ2vmQ5UyL3DnJZqAq9F8wiMuPQ5mdqZzL/i6EK/vDoeiZOH71+Tp+D5+xLu/j5szs565JuRJ6JjzPOAEPBmekf6g4a5h2VgFQETtg4JvNs1xGHbeAHurXGTa/mpp9+nO88ettRa9uxwjGdyUspbSHETcCzeBTK+6SUW47Fvdzub0JqgDC//Ta0X4hb+ihCiSA7PwJuFyBBukjf6YiiHyPEoT+CYPGdpHo+i4qLrkivZsAo3sgMXTtbIxqgVE9ze806Xtk1gXsfPIn/6ipkcnkXN52zhoU1B3LO13TJ7BPifPsPdcfcRdOHOaEObDnUAPmFzaUVtdy/0EAZl6JtdYRfvnQC1q93kk4OkltIS/x/6sC6wPu4goqVVznSlbA7FUETLhN9vXn7uP1NP+8tqufx3smYA6iWunA4PbKfqO3jjVgF5xY1cEV5LWHV4uXusfy5bTppV+WPLTNossK81D0Wc2cIuTPkSR/b4LxYgjs2hSixkTEF2aOhzkogSnKnogcrIekdIxHVOuqpvTivFWasWv9JmupgqA7fffJ0kqaBUZWA4+OeEREem0V7oRc7VgI5iwCJ4XP57XMbuHHJdDqa883+h0JNWjgFPpSEmTMWBook4yaZlFVb1O/MHyzPh1PO7+HLP/PCbV+6p4E1zxcS68n9ltT6NDiQvKmC8K2NSMtFWB4FFSnzzvClpoAi0EZZ1/XwcPCPZzg30twzjuOG/7mamSf0a+BPWTiR3W/tHXLsz9b/S9jiQyDk0aqFdxSwePFiuW7dukM+z3UT0Lrg4AcOgATStp/P/flKaltLOH3uZD57yVLKIqGDngtgxv/G/rbvkXRhd7KQC0oaDmroXQldtkGpbmK5gl3JCAWaxbbaSr796NmkrP4P1qdZ/OTDT7F4Un/GnWXCa89EWHpRTzbz9Z+BB9um8IumuaSlV7bPL2zG+WL8fOrLnLf5EgKKxfcnvs6SwlYuqpmLbeXhiQuIPjoVYUtKfn+AP9yxlpKKfmXM9b3lfKP+RJKud48yLcX3J73GlEB/ScGWRo1IiQN+wS17TmVTvBRFSFxXMNkf5Z5pK1GRPNVZw4Ul9QQydUotV9BiBbl6x7kouKRdFctUcf5RCvZBFrOKRD21O2vopQMo+Y181vinXUSnQ+i2RsxlEVIXleC+UAqugiJcDM0haFj0JHw4A+ICaA6iJgUIZFqgVfWgrLSwqcANeIHTiqJefKd10qYE0B/oxPdgF/IQ7KEETy1TesHbMZPS3P/qdl5+tIgffXEcqcTBXyxNd7ntF/s47SJvdea68LOvjOXZv5Tk/PYSSezHE3AnGoiYi/FkN+ruNM4EA+OxbpTDV94YsX+QN4Q+7J7hrpOP/nn3ym8xL0+y5MZXtnDrWd/GdVwi5QX8qf4X+P15CuQcIwgh1kspF+fd964w8snnoec/Dvm8vq5f85tL2dlcRUlBkIfvuJaQf6j/NP/5JrL3l9y3+3k+VLGLgDpyMLbPCDzUNpmfHZiHiovlKlj/KMNKDJ2Rzapu5Y+f+lvO+akEBEY3Dh01SAmbEqU81DaZbtvPmUWNXFhSjy5cLtl6IW1WgA+V7eRz4zbx8dNm0Lh76MstS1RS/1vDub69nNu4i0VL4xiZ8oXtlp/Lt50/IKsWQBJRTR6f/WQ2yL3jrQBT5yZRM4ftSkbYnSykijjKrhTzTkyQdBT0TM3ZgUi7Cvfsn8tDHVMBr/ats6IIekYxEy42UU/r8aiUO4KIiIUYl5kRD7CJ3i0l9Dj4f96BsboXVIl5epjYnFmQ0lGEw9fft4Kf/ONkepJ5Zs5CMv2cPewJFdBnZtx2nRn1KW64YA23tS7B7luAS4n2fJTQL1vxCWfICmr6ggTnXdWFL+Bw7+1jiXXnBqt9AYdrbm3mgze209mm8onTZhKPHiyg7a0k/rJhC0IIAmGPYbZpdZA7rptEIqbiOmSvIQOC1PVlmGcWgCrQ3ogTWN6G0pEvgH1ohvhQMNorl40rob2xc9j9xZURHjzwm6PWrqOFkYz8v5xdc1Sgjjms0/p46fdd/zBf+9t7mFzey8p1fi5Yes0ozzdoS1RzXdWOUd/vzd4yftY0L5t4Ix1wkvl/hj1tgxQMBfj/iUl0fYOSEDAv1MG8UG7SlekKLimt43fNMynIMGuu/+oBvn9TTY7B0QMu77m5lw/P2ka5noTp5FTnerpzAs4QJ63AkgqvRKs5K+LF6n1BN2vgAaYFepgW6CEeVdiZ9h6MIVxsqQwx8j7F5aTCFh7q8CinQoB6WjfOqlEY+i4D5/Eyz1IU28yadIAZahevq2W094Y8FUudTIRLQLFG8iuVxNdPQTboXqWXBCAkLip3PnEG6ggaRqkvt2C818G8qAhUgVJmsVM3+MLOpSiRASWhhMA+N0LPiSGmbmqi4/+xd97hcVRXG//dmdkq7apXS3KRLXcbjDHFxmB6J0AgCSUhJHESQv0SCEkgEEICKSQhEEKAwJcCoYROKKaDjY2Ne7ds2XKTrC6tts/M/f6Y1WpXu6tiywT4eJ+Hop079965M3PumVPeU2vDfLIbkFzy/QYu+G4LNodEVWHCoQG+e+J4ohGwO60qWjPmdnPO5S2sX+bmd/9TScA3MPmcVFV85QVcdNhkrrxjN8ee1cE7z+dx740VhMPEzFI91muBCEpcf2rG9afm5H7SjGSzS879VhPvv5RHQ709TYvBI13/gxuUAkwAACAASURBVOmtvbGz3+PZeR+zhjUM+EwIecU+CRMnMEg60wQIK7+FX13wRuyXDzEbbwe8kP8oin18xnOl1Mkzbx5SOcF/No1PzqxUAFWCnvoIRlujXHzYRL7xkwaOP69jULbg4cRAY9kVSZXDhyIkp+fXAzD7tC6uv3snD/+yjIaddorKonz1+kZOurCX/rWveGuOupKI1nqgS0F9KJsGl4sSWxBDF4SDAoerjwB3mYydbkXAqIpF1JbaFzRG+rygCiiT/JiLB+FIj2nt6hQftR4PW/CCAUaLA6U8nPoMKKAc1g3jVYxFuZBgxjBMFcPsFYRJg0jYO34i3kc2oW0MEj47D3VzCLNQQz8ii7QPm1dl6+xKbAEfbrrJLdTparPxg3PHUj4mzAXfbaakIhL7chVUVge5+le7GTUhxA0XVLNtnSu2KfcJu3TZrApUxA6pCr6TxqMXZRPd5MWbtwPTUPjjD0cQDfepxTtEaDaT0RNDXHRtE3t3OGioP7AYeakpcdK0odgqFEWgODSi4fQhQX/6hNjZh4LPhJA3Q++xPwK+B+mFWRe0nYVZ8CyKbXLa87rbX8Q9xHDKlmiyKUMIEOMCyM1uSIywiBq4lu+mpcHOH66vZM4ZndgdnxzTGlgEYOsD+fy8ajGlCYUxjjmzk2POzKwR9V3vmZ4mXmwblcKRI7DWq8AWQhEwsiaEr0NDKEZ8LaS05J4np39TWVSq/LulOmUesqAnOSuTYDIR5WHEmBDCqyNsJIVZKiPCpCtRIASggsw2cB7aQXhpXnJ4pmZab18oUbha/9UrcwmPKsTxXjPakoDlzNEE0qHg/3UFZkWyOVFKgdmh4FhlGee7O1X+8498VBW2rney+LUcvnXzXmwOiR6FbevdPPXnIrK8BrVr3H0EdOyqbSpdZ07EsX4fkepChKagF2bHIwzCE0t54akygr6mtOf3Rc8KSwBNITShGNuezjglw4y5Pr55817u/N5IliwYXPSL7FlohaTMW6kpmFl2RGco3lIMYuOx2TXmnHcE1/3125ydlfo1X3NENS7X4J3TnxR86oW8GVkLHd88eAO0XopZ9DqKmqZAgpk5fjqT1n20t8FijkwISVTGBS02v83ZYEiEbuJatjNeLi0cVAalwUszvaLXF4YBHc0aWV4Tpzu9cIwaEJA2vGo0o5NREwbXlK854K+L2d4Gxji72BrMiRcrcSo6czx7uap8LY6YaUOzQZZXZ+cWJ958ncIyHUUhrRNaWkoxIVMlIlV+sXMmO8KpceQDrZdySDeiKpw5s1mFNMFHScf1EoPz5q7m6fcSggN0BeHqRIYylDB02EDSW5UqKiFk4LqzAf+9I1Payy1uAqNqcGhLqagOsavWhR5jtNQ0g0f/UByzlVtY+J+8fq87UpVL1rt1hKaVY5SnmaNpsmTDCGTX4Ei8BBAtcGPkughPKYtXXxL+CO66Rm77+yoWL/Cw9M2hca93njEJx842q/qUsKxFoQklHGrfgk2DirERXn00n/42cofb2jTHzRjDNffPx+Vy8br5FLd/+S4WPrMUu8vBAxt+T+mI/oukfFLxqXa8Sn03suUEhvZBlhndhsob7VU0R11MyWrlCM8+K/tPKJD3NxRHb+1LM/gidF6PlKnUBv2ZVTp1OxdtOokuwx7PuLRLnXHv7yZ3mcqaRVFE2EgpMXfnE1uZPtufROcNEAkJDAN+//1Kzv92M+MP7T/e+e3ncvnzzeUE/VZd2HlfaOeqO/bEnaBgKY4SkbEwycFA2FR4umUMr7aPxCZMzi2o49S8+kwlNzOiR7h36TZWdBfy8L7JbA95U+L83UqUUluAxoibroWF0JKmUHlOFHVOB/1H2VprpCIz1w+WEptiEm50YC7JAylR9/lQ2/xEJpameVgk3ufWoPoiKIHkfAhpE/geHoUs0OLXiwTjxSIwJceuf531i7OQST4OiSvL4Kyvt/DUn0utCCEGyDbt+R9F0D13DJHxfWobR3S8/9mArcnXTy/JMDWFrrOnYOTEtGEBakcQdIOcUlD/uREzMPhMchMIHhqjfNZUlGAEtSNI9vtbOerodvJL4Myrb+Ku+c9Rtzo9B86v37iFkD9E6ehiRk/55GfcZ8Jn1vEqO29kuAS8KWFTIJ97G6ZwtKeRKkcXr7VXcox3L7sjHiaI7yKLP0IIBTO6CTq/D6S+nwPtmTlahEcnvM4TzWNZ1FWGv04S+Es3u5dG2U0Upc+r53AZfOEbLRSWReMcLoljbl7lIqdQx+0xeOC2cn7xaB12h0RRrdC2xOSoVYuy+P33K5Ocou88n0c0onDjn3pfAgHDmtU7GDgUk4uKt3JR8db4bwOtZbrNVAh4o30EN9cfSdoEJCRXla3hvKJtGKaCppg8XzCG3z58PGYfv4Aojg6QLtg7QQNhSZ3kcPj4pKJSRRTrUNWN2Ook+7060A1LyKdB11lTQYLaFST7zVq0tkDvkCEDKWNRMAYYb8S0ckXQUGfvI+Ctqw76VVbXldB1XA2uVXtQfCFEPxWU4j2Ykuz3t9NZkI1RGPNpGCZKIILW1J3mYjND0U1ynlmDXpKNkePCtKsEZ420io8s2YErlKmOVeKDYBl99Fw3nedOTaqUpezw4X1nG0LA6sVFHH/RHMbNnMNfVh7DheXzaW9MLqr+h0U/Z/JREwY9/08rPtWavNk4iX5zpoeIqAkRqeJQTDQhiZpW+bRbdx5Ol+7gdzOvxemcgtn6NYguTtvHwLQCdqSMIAS0Nal8+EYOm1e6ePvZvIQYZUvQazaTP75cS8WYcNzZ2Ld/w7DMFaGAYPtGF/fdXM6Xr26ielKQPXUOCsujjKyxbLU3fmkMK99P/Ry22U0eW7kBb17/ZdOkhO6QRpZTj33h9Ns8CRED6mrdPKFO5O1gJV8qrGV+2fqM/PdSwnp/DtWu7ni8e7o2fecQMFRuqZ/F+12pWbVSwqXFm/hG6cakPoOGyt8XT+fBN2eRKLTE6ADKFH8/Jp1UXTiLKH5DI+2FSaDdxPOtnShBS0PvmjeW6Lii2ICJjUV80iJikPvocpSoERd3UoHg1BJCR1YnnCEp+/tCwsF0se6S7lkjCR9aAV4d9+5tOP/VOigRLYHwuCL8c8aAAmpbAM+Czaj+IdYu7nN17V+Zgem1fFTeZ9Zga05fYk9RTUxD4Mo2QAoKR0RYdcxxlpc98QGQEm9I57zsfI678GimHjMxqbqblJK9dY0UjMjH6fx0k5/1RX+a/Ke8xuvwZgRpAtyKEQ+/sykSu2Lyo4oVrPfn8vD2tVZDPTP9qaU5Zw7J8xm9wsWbZ3DaRW18+9a9PLxoE4VlvS+N26tz7DntjBgdToom6dHMe4R9jz3a6ZaMmxZg1IQQt10+mq8dOYnb548i4OtdI4t6Ns112yRtTb0fdf3t+7e9MI9Tf3kJ+hD2VinhqQ2j+Obq43i1YyQhU6PDcBBOwxvf87Xyams5L7RV4zc0jDRf8FLC7rCbkKkQNhVMaQnrtzsqWNxVgl2kbgxCwMXFtSmbhks1+MqstfSNdJF+MYCimnpwbFYHZxfVxYu4920uMOMCHsD79lay3qpFdIchO9obhpkwaakIwuMLkS6B5xIn3kkSxQT36n04Nu7rbdsdiT1D6W+gkecCIVGP6sCY5ADn4HZpAThqm8l5bi05T67C/e7WIQt4gHFTAzzw9iaOO6cDzwirdGJ8bjnODFQHksOP7+KFbWt5bMVGnqtdR/SCiVZIXBoto8uhcfW932Ta3Ekp5TuFEIyoLvvMCfiB8OkW8q6zhrW7TLwvbjXKbG8jL+6N0eDbpvffUdEHoE5JeyiRo0SL7QWuLElugc53fmZlt2p2yZe+18QNf9yN0z34Ly3NBl++qinhb0nN9F7n8KSZfpQ0CVtSWlzkPYiaSkZBf/WJS+jaYfD6v/OHxO3y93Vj0aucSJt1/W91VKRtF5IKl24+gRnedq4dsZpCexgjlrzUM96+iIuLN53EJZtP5sINp3B/w2T+2jiR7207lp/vmomOSpXDlzaU0qOlF04eW0+UTQyKRKkJZXQ6Z8JqfyHrA/npv3KkRFuUrK1KYqX9PE5EWTS9fLapRGbn4vvf0ew5fwSNV1bhGmUdcn20E5AII0LB2i3kFqbbfSWKHfRSL6IwCioYh7oxRjpIE7ma5mwLQjcIHDWK8KSyIRtJ7U6Tb/10L6PGh/nxn+t58sPVOGy9cw1NK0+ueBWH4Nrf7MHhkrhjJTC3NBamXycx0Kb8/xOfaiEvvLeAUjJwwzQYioBSgBsrV2CjCzO8GHJuytzYdhiKmoNS9AyiZDOoycIsV0sfraJqMOsEK4VfUeD481I5zxORyVRSPCKC3WnidBv85C87kpKHLr5uHw6XTCKTcrgMLrp2H3anxdse1hXebKkglIYwSwgo9vqRThsv/r0w4xom/i4lREwFtiU7EH2GnR9sn02XbouPFTUFN20/kkuLt5CvhXDHNO6e4uedbSpBv+C6ujnsCHsIS40mPYt/NY/nr42T2BDIw6noXFi4lTtGfYBDpAq8LYH0MfFb/TGWzN6rRbjTm4kyRtpg8tPKpfxvzVu8MuVFvle2hmy1h3NAgt/E8WBvUpCMRYP4YyX1ZFRAuiQp1cQ8QkN6VHAo6CV2nF9wWSazkI73iZXkPfQRco2P9UuzqRofRFFNhCpBBTNPo/O3VahndEJO1Lr/isB/xwj06a5+BbYU1hdA22Wz6LjoMKKjC4hUF2A6VcyYV1zSG2HkdBuoqkSzmaiaCUgqqkP89KEdHDK7t8aAosBlc3rZG42ibHwn1GC6bEkafdXkCvInLwf3N8D5FShaxLxpNRkmK+O1Yj9HLz7VjlchHFD4PLLpaNIFK/dof30jUvoeH4i5UQhQhcm3y9ZB169Qip7DzH8B2i4kOT4/C6LrMBungDrWejCN5pS+MsEwoKA0wi8eq6N4RK9QbGnQiEYEpVXpN4hEaDb4xo/3Mu/8dnLyktdkxJgIf/xPLY/cWcqGZVnkFel8+aomjvtCR3w9DEPw0dKRnHxmqklKSmjzOzl+7l6uvH7HoAqmiFhw9GXjt3A3RyW1W9FdzBfWn8aPKpdzXM4edFOyrSWfY0Z9iK2PsBMCPLkG28Me9oazUvnfY2Oel7eVK0asB2lVrwoYyXbz3++Zzh+r38euGKjCKkAUlSormopx2aIEozZQTcSYIMJlpg7QD/635k1qXJ1WKUh0Li7ewhn5O7hu22wO87RwXvFmvl86nraQjeCVxeiHWWUC5T4D1piw0wk5upWBa8bGU0zINhAlCV8gLoWWMi8KQYvIrCOU6Elg52Y30g7+G8rwlhh88ejdHO5ZTEMki3/ljWNrJNfirncqhOYXk331zoQathKbw0SagvLRYcZMD7HezKPLNJGGJbSzFtahSIPomEKEL0KWx8l3fvZljpnTzNJn76S10caEGQGmHeXv93m9/JgVLNlxLKu3B0E3iZbnEKopwrW6l6/ppn9dh6K6wPvD+G93XnUuC+bfZWlfPQPENIu/XPvFAe/T/zd8qh2vPTB9fwD//SQK+qYuN9985BxOm1rLt4/7KK2g16PWs2EbHFUNUVNgUxwopWt6xzZ94LsXgo8Med6JkNJyxOYXGXFHn5QQCQtuvWwU7c027n6pNiXbc6hjvLp2LO9sGs2dF7ye0RRhyvRfzlJCi8+N2xEhyzE0h7cehV/WzWAreWwJWtEgAhOPGuXfE1+luS0bkJTldOOypy+EIk1Y4S/khu1H4zfT3TRrbf42bgHjs3zcs3sKj7aMp6+AHuts5/LSjdS4OtkW9FIf8nBx0Rbeaq7klo/moHtNXN4QJ+bu4pWOUbFiHv0L+TGODh6d8EbaaKuGiIv5tcdTYAtxZGs9/whNxszpdc5KEwgqGK/mMHvUOlZ6RhKot7hrREUIZVwgOYxTNylc3U705swcK5F5HlzXevjHIW+RrUZxKCaGhIipcvvmGbwZqoxrN/ZHWnA+14HbHuWeVzbjcEJBqY6hCwxd8MyDhfzjd6WERuQhK8G5yFIKIhMKmfP9M7nm/GMpzs3G9D0E/l/3u04pKFxId8TLWy8v5y+X3YceiGACxnQXwTPLKMwdyb0XfYnRZckx6lJKjvr2H4j0KAOm5HffOZvjZqRWSgvoYR7bsZC2sJ/zRlSRHf4n3aFl7A3n4fZ8mcNKv5Riv/+04TNPUAYgQ28gO66CmMPrkge+yJbGAo6pqefWL7yJx5nKv77oFS8z5vpwZQ28BsmRHNmIklg4ZfdD0D3EB3vA/pPRUG/nxxeN5s+vbxmSjT4dOgMOavcVJLFbDmZuUUNhU0MhE8uasWlDm0PPtZkSdKmwM5zN/9TNZpTTx/UVK6l0+GnrdpCbFc4YtaNHLZOW39A4Y/2Z8aSpNKORo4R5bdpLmCacsO6cGPFZb6cuJcqPKpaDEEzNaqXYFuAnO45kSVdpnGkTCaowMAZw7ksT0OEK1wa+OmVD2rkHDZV5a88FrBKGRhSwJ++iMgq2ZWEq5oXZE85CYBJJvMbEjkMmIx/ZQceLmaOhwufncsVNuzi3aHvSV9ETTdXc12AxioJ1U0SHQd7VdZx2Vivfu30Poo9PMxQQ/O3XpTzzQBH2Egh4nSgNUXImujjlf8LsbM3ha2f/jLFlXmgewF+VBGeSwgRw1i1303j4vuSYCr/CU3OvY1Tx0JORXm9Yw02rH0cCxbYAZ+fX8c+mCYSkikCSJaKMcXbREM3GYxvB3bO+yYq27Tyw9Q2QkpkF1Vw86hhGeYqT+jUMg93BNspcOdjVQWqJBxGf2Tj5RAjnicjC16DlRBo7s9nenIcpFXa15aBlIIN69V/5TJ9tEToN2H/Sy9uNbPs65P0Ruv8wPPMXmQV9QUmUkF+hrclG+agD42dVFZPRRe0DN+yDQNjG1IqmQfCoW/9NimyjJ/beIhAb6+ri+UmvxNuYEiKGmlbASwl6VGDooGqSbE3ne+VruWfPNKKkI9QSccpnRYHHq17lyk1z2O3MRUEyytnFjyuXMzmrdw1ebqtiSVdpMqeQwKIBHuB6hQLSEKzQ8rkYgZbmWWrXe4WAIZQ+/PA9/Uj0I+3sCPdEfqhIIDsSQg8Kwg4NYQIqTNywl90vptZ4jfclJHkNPmbnNCYJeL+hxQR8IneSQPEKpt+h8O2T9qCk2dOcbsmXrmrimQeLCEzIJnRtMV8s3caVlYtRhRXbHjHeIRx8HId9LkTeSzOrLCCx7q8TCpb2rothsK2xjcaZloAXIsLR2U3sjGSzi1y+uuAvvHfJjzNccXpEDZ2bVj+BjD2BhoSH9vUWh5cIuqWDNcFCAJr1Vs5691ck3vQ9e5bz/J7l/Y4zwpXHE3Ou+UQI+3T4zAh5AEWrwsx9hFDLdXHnYl1zPhv3FjG5ogmHlqz52OySh35exvd+sWfQJps4oouRkeUgNJAHTozdk7iUDkJAKKhy+/yR/ObpbbjcZtqXcSBICTbVwGnLUHAzA4SAHHfm1P5EhCXsCOUyytmFKRWiUiFbTV2fJLs9UJgdyNj/tg1OisvDON3SikEHxrk62BDMo68UFpgcmt3rB3Gj47+wmYqSRi79RwdnjN+TEsL+QuvoZAGfODGs+HOZ+ENfmIIPXphI0+gVFNuDSUqFlPBgQx/+8XS7eaJ9uWd4AX6HExzgDEVwRCMU+ivJz6lkN++mnwuSgpIo99y3npagGxKokjYG8tCEJNxnHzI0lbbxOdj7oT/Pybc2FdktmZzXztz8BnZHsuPFXTTFpLPxa2gjl6OG/wbddwNhEEWQ9yCKfSKm0Q3RjWCbhKJaiVX3v7SYB19eYikH2VHU4+Hv4xdQk1BHQALXbjkq3bT6xQt7ltOboQatGYq19w2dHSr2BNu5cOHdPHfs9UM+9+PApzq6Jh0U52xGTnyf7IQY4Gv/dTpvbhhDRLfiqXtw+iVtvP1sHi//swBzf+pyd1xjfWcPA3reb91MfgijEVjxfjYBn8qurU5CgcGHifWNctENBU010fZjg8gkgHvG6LHl/2XvVC7bciI/r5/JMl8REZk+L6hv36qSOeLpg5dz2NnuYovfy7kbTuOevdPYECyIkU4ln+QQJpeUbInP6S8/K8PQBY0XlHO/fzptUSc9NbDjc88wL2lY+/cPKlZiTxf33tOmwYGMqMx/7TQ2BfMImwqRWBiqCfy4agX3jX2HUltMkxUkX+wgIkJCTjududkcP+swNmxVMLyOPvOWgGTyrG7uebWW/GKD6lwf0YTnKUeLkF7/l+RokX6nsXe7HdOuEJ3rYXMwj+vrZnPJphOZs/o8jl39BX6wfTZNpoPfPnkLm4MFmEXLUUo3o5QsRLFPBEBRs1Gch8cF/POL1/HAf5b0LoVdcmvVYmpcXfFgiJ6oyLtr0icf9gdfNIhLSfQdDebF2T/b/N5gO0HjIFRBGQZ85oQ8gKo6uP3yL+G0K9hUk0DEzh0vzePSBy8gEOnV2A471sdF1+7jo3ey0ffr/oQZroxbIcAwBa+vqyYcVekO2QkGFLZvcvHbay1OjXnntpPlMTNGC6XrswfbmnIJ60r6UOQDnHfPfwVwRkE9d45axK0jlzE3p4Ei2+AWNl2EU8/LH3YpXBM6gctqT0zi/JFxh6jEpUTxqBF+UvURk9yWKaZVd7L5zJHo1Q6ix3loU91ctPlk/tIwhQ3+XEKmStQUnJS7C2eacEt0gXg3h2Nce7mr+oOYkJa9m4MOhBXMWjeYgsYdeXyz9ngu3nQSIVO1HNjCSqqb5m7lgXFvo0V0tA/9iDZrvHwtxHlFtRzhbSRXHbjO6rItO+nwBeg8/xBCU8pwFKt4Zns4/kaTZ7au53fP1ZFXZPXdM3YPqh2d5KlhUra1kEQs6eap5mrCRupmGwoIHr6jlMoJYczjsghLjYC0YaBioBCWGkt8pVyx41h2tPqxt/yC1r2Hs6NzSb/XcteTfb5G2jROyd+T0i5u1mvMEDqZAeeU9N0IDy52+1sHbvRfwGfKXJOIWROqePqWr/PswrU0tHYxa0IVJ80oxq5Xg+9uIIoQEb50ZTMXmDFN1EwvbPpHj8XZCQylGHIq6przueM/x/Knt45kQlkzDe3Z7HhTxyn3YcvVOfuylv12vI4t6UibOToYDJbHXggY6+pibMKn9oGgZ0zf+YWE29IQiMWgIvlj9XtMdHckFQsJmirr8kuQv5I9/nh8hp1/NE/gH80TAMkohw+3EiVsxBLAFOJtjWVe1LDKy6vGc9ns1Tw3+RV+sWkmz28aj3SZyCY7cqczVkJQIhzWAh+a3YImzKQNVVMkWYrOsc3bWfRRDuqWEEdeEWSmp5m79h6acDXJIZ99sSG0k4jNg9roI3DUKELqSJw2nZcDklf+OIs/XPQy0ysbU87rCRd2EUV0GEinYsWPqgLnX1tY+YbKovZxrDq9iFurluJQTQwd9u2x8eZTecw+rYtrTtvD/S0Onmkdm9o/goipsNHhobUji5G5e2np/C6G5yPUDLZFf7ivAqAMmS6jP+SqLdxQsZKf75yZGnJ7EDAy65PJUvmZFfIAZflerjh7dvKPjsuQ7ouQ+3ozUgerGWeGhKzLwf8IVgmg/YPHGcYwFRo7PTR2xjhmpkB4Sjk/PuMdxk4dGmd+X+GcKSxyQGdq/F+xLw7DWrOPK+pscVc5/Qk+Exjt8CULeEPl2ZYxSKFARh5+YdEPSwldYGz0IHINiCjIXXZs9T7QTZYUjeCy2asBmF7UzPOvTcfstFmZQi4DURKCqEBUW/d+hN0fT+RKhB2d4kkGYVsuMkvlA18e7/oq0lxbZkEfyQ6BPQvD64gFxygEIr0OpWseO5075r/EUXnJTnIhLCfxVSPW8NOzypGlNqRHRd0aAhOiR2QhDZPJ7lYcsaxoVYPykVEu/UFvFvVZBTuShHyZ3c+15as4wttE2FR4rWgkVZ52FAHZapjatteYUHh62mvJctrpDqZ+6WUinhsybBM5Lb+RNd11PNc2BnkQBf2UnMrPHa+fJMjuvw1/p/6H2R+nTSLKcrsZV9LCxr3FGAkk5dVFrZwzY9Og++n53Dbl8NAFSwQ/3j6LU/N3McrRxeat2YzT2qkaF0ZLeIIOVuWq6ypWsaK7mJfaR9FtpH+Rugx7rH6EVdpuWXcxTzTHYqZVAeF+diYhkCGg1Y5sUlCbu/G+vNzSdIEdbxlcv+NQNhRPRjcV1MIopgSlKmwV3jaxCleogCHZ1J2LP6ri1gzWBfJZ3FVKlqpjf7eT136m4fHVgyKInOol+o1CizRpsFDAlmMSjdiT7CrVRa2MKW6nucvN71YewWPz/oNdJH+6KQImZHUQPXkC9jd9iB0R9MlO/D8bAUhwKfy5YSqdhp3vla9PP37C4+RRIjxS8yYeJYKqgFMxOLdsW9xEZCKIGJmLx9xw4Tx++rfXkn77qK6YmWOa0rZXSrf0szCpENpYdPtsJrrrea3DIGAOnO+wPzi6sIY/zLxs2PsdLhxQnLwQ4jfAWUAE2AZ8XUrZIYQYBWwEeoqfLpFSfmeg/g4kTn4oMNuvhfDL/bRIdeh9XGj2ubnyn2eyt92LqphEDJVfXfAac8btHJQA7bmd722pYt2uYr557EpAYtdSee972utRK1M23XFDwkuto7hjd0IIbsikcuk+7vnC0jhzpTNr8L6C/UHQUAmYGpdtOYHmaGqhWwXJ4Z59lNiCbAzmURtMpi8Qu0LICkfGXcimG4TfK8DsVMj7+3KUPuXfpKbQefYUjKJsVMXAHBW2GCr7BGbIqIB1Th4/5xke8U3ivc4RhKWKfVU3jp/t6y0CAkiHIHKCh9CVg6HmiGn3EnINDy3/sUJhHJrOXV96helVjZhSoAhJrS+Xmrw2nEqvkK8LenmwcSKr/YW0RZwQNsm6cTf+X1RAdrI5xano3DV6EYd5krO1A7rCd2qPY3MoP7ahmpxTUMcPKlalmD1hIQAAIABJREFUda6HTBWzcCHZ9mQzxlXL/sqy1jqEEEzpHsvKNzswYw9ucU4Wz373tzhSOMRuQyn98sCrpO9C+h+C6Fqw1XDPrnKe3ttIyJTYhUHETBfkaiHdo2H6FAip4NVRFEm23YFUIGBYdBUjXPncO/NyyrPyU0/+GHHQkqGEECcDb0kpdSHErwCklD+MCfmXpJTpWboy4GMT8tGd0HpihqMqovhDpO8+0FeCOhVCT3Gg9vahQEqoa86jsTObaRWNeFzpI3gMCc+2jGF9oICLijcz1tmV0s9tzx/LxUevZVxJ+uzIvhz1fbLEkcC2kJdf7jwMl2pwbM4egqbGq42VtJ/TzCGzfJRURJh/6x6yvanP0kDa/VC0f13CWx2V/LT+iH5a9cyht1On0Lmx/CNur5+JrqX5eJWWAJUhgfKkJPuZbSjRPg4MAdPOiHDCVVFeXlPDklIPSkHmZCQnUQyhxJ3EWdfvQlufam6TNkHX42PANfAOmaVE8Jt2FAQT1kxhzfZGrj3pA754+Dqctt65hA2F3eEsyh0BXKrBhkAe82uPQ5cJeQVSQrcBTgVsfceWnJS7ix9WWtwyphTYhMHde6bxXGt10g1zKjoXFW1hftmG5B4krNYvZkblLfHfPmzZwlXLHultFOvHpdh49+SfDXj9A0FGNyPbvgzSCoiQqIRMuHbbMaz2W7Hw0mJmiI1v/SPbBEQVlFKdeAx9RGB86IUOm8UnZAoYHSBrjEHYFU75IHh89tWM8aSvDfBx4KAlQ0kpFyT8uQT4VBBHKLYqTPKANElBnl8iFC8i50YAzH0zSS/gD562LwRUF7dTXdx/0pIuFR5rrqFLtzHZ3Uq1syueCNTTz83nvEtrd+a6lH0dzYlsj4piXeU4VxcPjnuHKAoOYWAi+HJRLf+8rpSdK+ycdnFrWgHf038mDNW8owmrfGL/SI15LrH7OSa/kbsci7imbm5SGylB6gKhgXBJ1DE+hCah774qIU/xc+rUncwdv4PXWqr4VdOMjLMIYUt6PJTGDKG2KtBlDErI+00bSIlQFO6/+gJm/889nH3oxiQBD+BQTSqdfv7dPIbzirbz8/qZ6H3pJoVI0eATDvJmRwVdhp1ILBzUrkhW+gtTbljI1HiieRzfKu2T7Svg0Iofxf+8/YMneaFzZe/YCQiaUV7ctZyzKg8bcA36g/T9AmRvwpXAwKXA9RUruGTzydZvSqq/Q+RL4lFyUiIRGB95oD3md+kJQ93pJDSpLe0z+72lf+WVE35yQPM/WBhOm/zlwBMJf48WQqwEuoCbpJTvpztJCDEfmA9QVfXxld9SSj/EbLkI9J4vBw28d6K4z463McNLQQ5PpMhwwpCWgP/97unUuDq4ZeQybMJIEvA9UBUo9g7tKyRdhJEqJFqMo11BognJN67e22OO3i/sj/0+koaDvp8RANgbyeb6uqMosoUo0oL4DSsEsKeN0HrnYkx1pY2KdboNZp9u2Zfddp1Ti+t5rnMUm8PJn+lSAkEBLpl0fUaNE7HEn1TW0SzQ8N9UCsWDfQ0FCElxIIrTqbHwd1eitD6QtqUmTO5tmM6fG6cSzVSEVlgUzulug4nCh77BaaYBU8Pok+0rRAFCWP4TKSUvdKykv9CZ3258IUXInzH664Sa/KDBpFMnc88Tt6Q9N47IypSfDAlNERcKJjZhxugc+kBY/4orHWGg1U4Kwb3HJNMD3xrx83rdOuZU1uAacmblwcWAT5cQ4g0g3d3+iZTy+Vibn2C9Go/GjjUAVVLKViHEYcBzQojJUqZKTCnlA8ADYJlr9u8y9g9K4WP9N9A393PQBooHZLDnzR7OqfWLBe0V3LP3EASSpye9ilPpv6LTUDAYZsnE38RBcramQ8hUeb51dJojqSaaRESlygp/MQoyIZTO0uhSYvNzNUJfzcf5zzaISIS0BHzN9CBzTu91ItqEySn5u6hv9BCSNtAtDdBcn4UyOZV9MXRJAdkrAphRiXF4FkaZjcj5ecg8dcgL6HdFqd3TQnWJzlJ/Pod5mpNs4qaENf4CTERKScO+GI57V2wLoCbkDwgBFDwdP772/Y39Cvh0OMl+AehWPIxEsPGpdRz/7pd5q/HxzCcp2WCG43926ja+XTuPfVEXJiK22WWeQ3x6dlAmdWOuy05ur/c3f8lPNj8Km+AE13TumDew/+DjwoBCXkqZyXgNgBDiMuBM4AQZM/BLKcNY+yFSyuVCiG1ADXDwDe7DCcdx4Pt5+mPaBETBE7GNQEW2Dm8Bk/6wzl9Im+7kwsJaxH/JQQyWlqRw8KJqemBKiEiFVd0FPLwvtSanholHjdBuZDZLAX1ipXvMbakTj5yfjz7Jhf3VLioiXXz1gj2ccHZ7Eje/IiQXFG3Fq0X4z9YKVmytwtibhVIdSqvpmaMd+H5fATka0iEsgjKV/Vg4QRd2mju7uWPbH2nXZ/BwzVs4FBOnYhA2LSqJX+/ObEoabuyLuvlp/eEcktXC+RWTEbm/RiTQZjbtbIEBQsivm3AGYGn9Vx19Buhueu5NzwopTQZ3/ujP3HjHd9N34v4qdP+ZHvrv3+85hN3hLPQY25nZzz1PhBDAyBAiqCK3JTj5fYol6PsS9CU5teDN0Gqe3DiaCyf25zv6+HBA8RBCiFOBG4CzpZSBhN+LhBBq7P/HAOOAugMZ678BRasEW7qXRYD3NoRQEbZJCNt4cF06pL57bN/74/eel7uLb5SsZ4yzC1XsZ4bTMCBT2eXhhiJAIGnTnXjVaNxsBOAQOkd49nHH6CU4FR2Rpq7AYF7svjAnughdV8LWH47l1jHzOGfTGTzZXJ3kr7ApkjML6vlGwTaMDR4I2Czu90z1C0Y5kXkauFXLwTBkAW9RFyBhVHke6wIO9kQ8XLjxVP7aOJG3O8r5274JXLjxFOpCOUPs+0AgeL1jJPPGPoWS97skAQ9QM7PaMnP0fdhjL4BDqHyhahYAi3bezq71mcvzLXjgncyzyJrPLvMoIqaCL2znrY6KuIBPnOugrkgDZVwA5YgO1FNaUOa2I8ozZG+nuY93b35pUON8HDhQm/y9gAN4PcbH3BMqORe4TQgRxbq935FSZia//iQj7zHw3QbBp4EoqFWQ8xsUezLplJJzM8HwbmzG2ylfppk03f4KmvSHw7JbmZHdSkSqH3u1s5731JCCfREnI5zB/dqohgqHIjk9fyfH5ezhsaYaXm2vwiZMzinYzheLtqEJyeMTXuMf+8bzfOtoq2QgCg6hk6VGadPTafmDWT2BiaBFd3Hf3qn4DDvfKN0YPyqlFfbaYzKSrTZkfhQxrBkoPZuUpYlKFM5b0ktv3Wk4+EfThD7th7axJT6j+/NlVuLModDlTXusasIIxv7BQe05kXhmXU/35bYcnjvRCnLYF+qkkmcx5ai0cxdABgohAJ7ZtYxfbSggXzudijqDSIV6YGqsXSJKrEI9wqkjD/MNbl2EIOrQeWXPSk4bcejA7Q8yPjN88p8ELN92CpNd9dgT4pMPtikjHbXvcPadqV/dtGopSwm6FCzxldJl2Dgxdzd2kT4mfzjntSfsptge6EvLDkBjxMUjjRYp1nUVq1jYWcbtuw4nZB645HUpUV6b8iJ2xWRTIJc13QVEXgnxh7ozrR3bbqIe3wr24bon/fkbMgnyoX+5ZB5+4AdMAE8dcx1vN27gnzveJ2rqzCmawM1TzsOh2Tn3lkeob+oAdMTMbkS+jhKRPHT45Uwb05s9+9yuZRyvXMZ915Xy5r9TGUZBMvOSWdzx9xvSzmPuglsImVYUk9lkA0OglET+OwxdUuLWnLxz0gDO4mHC/ws++f82zOgmxjt3Jgl4OPhOyYPdf6IOkDhWrLwnHYadb22ZR5vuJGyq3LX7EA73NHFL5VLc2tBMSWm56GObSCLRVjhW8MGW4dpL7UFujMV4CwFzcxooafBTH0nUNPdv4SSCVt1JrhrmLw2TWewrRU4RaKs60PNzLUqEbg0lf3iI6/qfZyYBL3ErDgLmEFj3YvvCnKLx5NiyWN+xC900KHHmEGj1s0/vwnAJNFWjNeqLn6YJlQdmzedHK/9FbXcvZ86CxjW8vW89JzfPiQl4AA35US4SiRQQPuIBVjeMYWLxV2loDXHvw0spOrGE6+7axaKXcwgFkqWz6RIZBbwpzbiAB1CKoxi1TsgTuNwRgqYt7XkHDULEE6b+2/hcyA8X2r+VxJ2SiIOtzR8sDObz/be7DqUx4o7bPgOmnUWdZfxaOYxbRy7rt/++bLtCkBIGKgSEDJVuUyFHjbAtlMNLbSO5qmzNgGu6N+Ki2BZkfu1xMQE/CBvaAJAS3EqUhxonsdhXZv2oAIeEUTw+crtMuvL1YVOkB5oL9L0My6zTK+BjiV5Rgdxnh9wIIqs3vNOMgNzqRtY7UaIackouN3/nLJQ0dsQPmjZz7Yq/Jf2mS4P5H96PkcDb3oOoNHhxz3Kgr6lMIKWkuXYtcye9xL6dD3LBXV9BNxTuef0oHrr8WZ7asJ7/vaOEt5/NQ3NICkdr3P3OMxnXQhEKIoH5H0AdF0IGBSe6dvOSf9TH5kPqgZbJOfMx45Mxi88CzH3UBnNSmB4/C8XjM8lC04Q9kSz0Po+RjspbHRWD6ren78ebqzO2cyomZ647k6NXf5FLN5/ESLuvX476Dt1GwNTI1yKoAr5fsYoCrU+2aSxGXOpWFqT0C+SAkaiSHDXMuRtO59Hm8UnXwUQV90u7yD+iFZGRL2j4HgZpgrnBhdxns+YvY9mcKRCYTTaM1/IxV2VjvpWPudiL0uzguLzJmAsKkbVuiKiYUvLu2jpO+dGDace8Z8uraX/XMbGLDItXmlmbbfe7cKs6q7aUoghrM9qyr5CvPXg+b28Zw+lXBbjmrQ6+tfCLKQK+I+znyqUPc+yCWzntrV/y0u7lzCuZnHr1LslO7aj/ShTaBVVDL3RyMPC5TX6YYDbW0BRxYldMHMLApRoEDRUDgVvR0yYqDRf+W18KUlp0vu26g+u3z06K6LAJg/enP5vSPtM8/bqKWzXSHo+YgnM2nEnAUAlLjRcnvUihLX2lKhkLt3QkmM10KagLevnqlpNS2hpv5UFQRVVM5EwfSnHmIjD9mqdDJjnnbaP7P2OQQmSgtt1/W7mpAw12zGY72E1EQRTqnch9jpjyLiFPR5uTTAhmhsF8tTDNuJLCHDctnenzOwoLTVpbBYqqcOLMsXRPaObD9tq0bR0xLv50dXfNFg1zUW7a8d+4/hFy3WF++uzxvLxmfMq5YCKmd+MarTM5t4pZ+dUsbNrMvmAHLbovpfW84kl0RAOsbN8R/63GU8YjR36XOa//9KCL+cTne3bheH4/82sHecRefG6T/ziglFJsb6TbUNkYyEURlnOydY+HE2rqEYo8aIL4v2UKEgLcqoFTCfCn6nc5a8OZ6FJBxeQYb2qhcCEyC/r+ErrsiuSJqS280DqKhS9spU1RKJqWvm3A0HCqyfZwTUgqHd2MdXawNZRAXKYD3dYrYFcNcl3dNElHvwlh6XQiKcH2fjd2l40xDS3UlheTKtBlLBkrVdjFek8/KJaAN9/LteYqYxE224Bp3ahTAhjvW76AuUV7uGLcB4xw+tkVzubPDVNYuC7zF1ImAQ+SlhbL7GPokteNZYiWqMWymQaGFGSpUcKGmnoduTqoMhYV0xOnDkdPryMUc+wUZvvRFAO9J5vZlNh2tcLpUeQIlYgJK9q2s6Jtu3V6SIAr9Tl6u2kDbxx/ExLY3LWXsZ4S8h0WZffJZdN5rWF1xrU4UEgJwqdw1cyTuaDqSJzaJyfr9XNzzXAh76+ASrZqMMPTSo29kxI9ym9fOpbL/3ouhrl/MfGfBijCKi1356gPKLH5KbCF+J+K1Bcq0/X3CP7+NiuvXELrb7bScHuQ91/IIRRM39gkfblBXQoKbL0mGynB3GiVoROYeJ1h/n30ixye3RgP88uExBwHKYGwYPxHXqbMmUDT933khYMIZMxEIFExubRoM7Oy96H1iePXhImtz28p4eS7nBBQE9LsY+GU67KRDgNlmo/jJ27jF+e9wdisLlyqQY27kztGL2Z8dib+IwFuvZ/rjI3lNqwwwgwCXmCiCUkg7thM7k/RQDmlFUYGICuKWhhGndvO0lEevrDhdE5fewZHTNnRa+KKGuQ8uwZbVjOyQgGb9WAIAbLJhvFqATKkZnxWHt2+kBy7m1mFY+MCHuC2aRcyPXdkhms9MEgd5BY3T516DZeOmfuJEvDwuSY/bFBs4zCLl0P3nyD0HHe8NJUF68dimCpnTN9C1FDR0hSS+KxAEXCUt5F/TViAKkwcSnrhkZEeYYD+pZQce+YGXv7bWJ66r5gNH2Vx5S93M2ZSss3Xqejopkgqpg1gV0w2BnIBiSIl5mYX7r0q0h4hyxHl3ktewqHC5aWbWFtXgCpIEFx95tKhgM8GThOzwYG2281vXvgWix9byKr3N2Ccv4fCYx1kHa1y5EldnF25E10KVEawvLuIRN2qL3GYlHCEp5GLirdQaAuxqKuMf3x0GB2GQlV+B5fPXc7UEfvY2ZbDwwtnsKHLRX5lFzdWv4fLlvwF41RM/n7Oi3w4ZQS/eGlebyEaANVEjAsg13pI3mOsdRPTfCgVsezdfm6ORKQtgq7sjuB8pAVpQuiqYpQpfhStm3K7n3K7n4+6SzARtBlOrm86iqNm5fLeYh/OdQ2o7QGCxxdYDJkxmN0K5rIcMAREMuumufZUGmoAIQQPHvlt7t+8gIe3v5P5goYAa4MHc72Hu876IiO9RcPS73DjcyE/jFAUN3ivx4wsJBCxYZoCTMnRZdtw2Q9cwEdNwd5IFgW2ENnqcIXoDR/UmPkmHQ7UbyAETD/aj81hEA2rrF+axTVn1PCbp7dSWB4lv1hH0JNIKpPGCxoqL7WO5JmJr+JWrXYdNU5W7izD6wpzaFUDamxTyLeFOT1/Jy+3pWp9Gia6EJBjYizMBgUUU2VCVQmKCCPHPMZja9djU00WLSvhkR/k8eTIarxenctKNjPO1cX88o280V7BnbtnEDCTNT4p4UuFtXy3fB2u2DpWOro5/Ss7+dETJ3P3xS/j0HQ0VVJZ0MnMUXtZ0FLJqaX1ST6IRCgCjqzew9NX/ouvP3QuW3bn4djRghr1Y3oFkUMMzFW5lk1fCsg2UGZ1Ity9uQ5D/gKVEscTbYRPzcGY4Y5/WpkIGiJZKEJy95j3uLbuGAwUIlLlg+LtXHHtibx82mZ8hkT2iY81dzrBlIiyCGgm0iQ5szhmHbtwAGfnd8afTHPEF4v6sZCtOvAboUR6tT4dJ6L3mCYlx0T93Hj1T8j3ZA1mZf4r+NzxOswwTRNav0Jzx0Yuuu8CjKd3cP116znpgjbSUZn3oEu34dUyO/0A1nbnc8P2o/Cbdk7Oq+fGihXxePVPMobLMSwlfOu4GnbV9obkCUVSUhHhR/fVU3NIMCmDOF4hCyvKKYU2PQO2Bz3cufswNgTy4nzwYH0llNoCbA96MV4tgCydMqWQB689n4a6c5lY3hin/dUNQVu3i/t3jOPmaauTrt+UsLy7iKu2HZs0rlPReXXKiyn+iYih0NiZRUWuLyVDerBrKyWsbSjg+8eOQugGIiyRLoGZq+G7oxLpsCGcJsLR297c7gQBSpWl0QuR6mdIq+ZHTeuQLb0NzqVE+dXIxSxor+SljtFJxw75SYTtK+vpengkssQWj4IyV2YhyqKIoghCS9h4eiI3BZxfdAQ3zjxn4MUAwkaUWl8j5a5c8h0eokaQFdsv4IG95WwJ5qIJk6hUmexuZaW/kDwliFOVNEazEFg+nm+WbuOkmidQ1PSZvh8nPne8fkwwfX8H/+0AFHlgwQ3/4M3qXJ6+v5h557SjJRAb9b6cgrc7yljvz+N75eszvrBSwnh3O49PXMD3ts7lxNzdsbjfg7tJ76+ATleI5MAnA62NqfbOzhaNsdOCKQKwZ1yVXiK1SBgc7qkgAmBsSztMqd3P78Ys5M5dM3incwSmFFQ5fPygYhW/qD8M2aGhHNmJoiu8cMnXeXPpM8wu35fE666pkmxXhKvGb+StjaN5culUukIOjp9Yx1eOWMshWS1U2rvYFfHQIyjHOjvR+9LbAnbVpDyNgB8KhIAppa0owRG9/OhhMKUD23t+9C96U9orlSGMt3KhKhR/VlORRtAPwMsjAJ+0cYp3V4qQd55dQtTZgizuLVUmBIjKCCKvly4i/pUhrOvACZWBgcN2e+BQbUzJrYz/bVNdzBrzd2YU/JrtHe9TH85GNzWW+TyU2AOckrubQ72S1dGzCEZbqMk/mRG5ZyI+IbHw/eFzIT9MMI1AXMD3QAg44fwO6jY4+fVVVVz7291oNomqSQI+hbyiPKCF+xqm0hJxcUX5+ozmTyHALiSaiPL76oVkK3pSFujBwlAFtC4F24Jexrs7D0iD73uulLD0LQ8BX6INWzLzuC5WLfQMOE7Pcc0GW9c0M+6Ed/EFVpDl+0rSmgcNlfWBPCa52/n5qKVEYqyOTqGzNZTDXj07KZv1qAU34TUj3JXrYao92cnptus89PoRPLlsKqGoZd/f3u3hybZq5hxSh5QxFTSGdt2BLQ3hnClhYyCfiVntKQl3Q1nfcFAB03IHB48sJjSrEoojKNNC6Z87DdSTO9Id6Rk9/c8G/UoWXSpMdLWzMZDXq5LHnN2rjuwmdEhZSteiMJr+WiXgBNmmUTkir5+5Dgyh5GPLu5OaPIsyF+BUfTdEV4FaDLaZHPUpEOp98bmQHy60fTPjoct+2MhZo6ezZkkWp365jZyCKJNnBcgragGgIZKFLhVeah3JWQX1/b64ioB8LdxvMtB/E35D49u18zglt54bKlaiDqXGRwxSwramHCryu3FoBqYUfPS+hzuvqExshSvb5OQvtbF5VRbhoII7e2AaBUWBh7aUsZyfEzQiVDjO4raRHzHO1QCovN4xkTvqa7hqxFrOL9pGVCoIYG80ixvqjk7bZ5ewMX/H8Tw2fgF6SGV1WzGHFDbhMnUe/XC6VQ+2uhPhtPIxu4BXOkdBPPpGMsuzjzPzd1hmArMPjYOp8lDjROZ6Gji/pJfMdSibqJTw6uP56JOcBH5UhpmjoahWeYeBaggM2aLbjxx0Cp0T83ZhSKwyjgkUvUgIdQQgJ9XhnTH8VrF8CebKbGZdWJly3oFCaBWgDf4L4ZOIz4X8AcIMrYCOK4D0JJtCgM0OV/9mJ6d9pT3tC1Vm97Mr7OG3e2ZQaAtxlHdf0vmfJmSpOiGp8VrHSE7K383MPsWg02FnwMUIVzAuGx7/cAp3vTYHgBxXiEDEjqpHmHfiIla/qhAJCybODHDlL3dTNS7E2Km1GNGBJZGUllZccWSEd5qCgMAl/NSHBNlKNuXZR3D2hFuZXmjjsrv+xb/crUwcvZeOVi/rugtxHB7ALnQifemMhZWmf+mKU9CdWHbiDnDsFHByG0pCkXSbMNClEjO1CcY4OvjT2PdwKgZOxWBb0EvA1KhxW6YbBfjjnql82F3G9o48zsivRzcUnDYdBZkxtDERpoQPukr587uj8f+8DFzKkFKyhvwMKlbAQVIGoJQUaEG+VrKZMwu2880tx2OkqOsCvFr6zziRWuAFrL3B2OJkxDwFp+1j5qf5lOBzx+sBwGycAXQP3M7AcmBl0HDe7ijn1vpZ8YzBHDXEbG8D80vXUWwPJ70rpoT2qAO3qscjMHoQdzSa7JcGPRzY4M/j8toTAMnZ+dv5cdWKAc8JGQofdRdz/fajOSN/BxN83Xy0voq3N43BkCoOLUqhJ8C/r3gMTSWFojmxGPlgBJIhSalolawpZtEeKOHZteexoaGUmooivnjMNApzsvjW4vtZ3VlPOlNF34gPGQFiAn6cq4MfVSynw7Bza/0sQqZGRCoU24LcNXoh49yWVr0pkMt3tx5LrhYhRw2zPZQTL1lntmnYF2dTntfFyZNruWzOKjQ1+f3tKx8jpsLPdh7Omx0V4DctZ2g66s6DgSR2O5jiaqXa3cUKX1HMF9HPOYkX0VOdpu/vVnozOBR+O+MS5hYn03//f8LnjteDALP9JgYj4MF68fsTPvNy9zLb+xxPt4yhwu6nxt0JEkoc4V6TZSxdX5cKDzRO4ttl61OEvFBKQB2Hqi/cz6saOnqEiikhLBX+sHe6NZdYHdh07SXJSp5TNTnK28ii6c/ERef5k7YQiGjc9MwJTK/cx8VHrsLWx+nWg8EIdynhjY4R3Lt3Gl8r2cg5+TvSkqH9X3vnHR5XdSbu97t3imbUq2VbLnLFDXDHdAwGU02AXwIhAcIPCBAIYUkCBDa7GxaWAKElWbJAwgIJNRAgptr0ajDgblzkKsu2mtVHU+49+8e9kmakUS8ji/s+jx7due18c2bmu+d85ysW9WT6t3Hp/HtAG4/kvtq8wHZYqsbq2MwBLf3QWnfaCj7X3cCfJrxHneHm6q3HxfiVl4Z9XFN0HP+c9ioezWSSrwqfFmFvKJm9tLjlqQionUk0RtxsK8vm0Q8yGJNTzaJpsbV4IkooDqaQ42pka2M6/10ynbUNOdbB5AF+8rf6UNYFclgXyOn2degCWwOQqlsjfRe2yxTg01iUP+NbreA7w1HyPSX4XJdP7cro0qPBBXlti2dFe6h4xcSLyc2j7YLFrmPALAItG9LuQvOMxzxwXdxC1P1B9EBNATURL1sDVv4ar5gsztrV5prW9uYm4q0x+D0R7rvgzT6Rs8HUeaViHPeO+5jR3toOcwnFjIbNIlTD80jy91BKcXXe0/y1eL5tsOn4g226x7nZ23CJyauVY9qaKOzaox/X5HNCRgmawJ2Fn/GzoqMxlRBUuvVgLPdYka82EVPn1hdPIsX7GnML91gJy0x4qGgqz4SmdLOH4rzvRNGeABN8lp98SRjckJkbJNtvctuEA4z1V2IGC9C8xwysrAcJjpLvBQn9UehzIOthNbDbAAAgAElEQVSRtilhI1sHTITo964LpOshzsku4rnyiXw3dwuHJlfEnB80NIoa05ji78hjI/79e4qhrARnt2yfx52Fn5LchSCyNu0GnoHk74GxE8xKHpnwDldsXRhTpEiFpN1CIeN91Xg1k4pwUozffYuMwoFIiwI/NLmCF6a8xrKq0SytHMuOulQaVrRKlQwYps4vnl3M9xesRuVEeM+d174ZpB3aqxcwKNEEVeABFNeOWsXi7F1Wj4SA0DuY7tlo2U8nVsZByMHnDzRo6KQycX8geeA6DPCDsRJKD8EsOwUzErW4KYmLvEvSDY5J38s1I1Zz9Yj1QIsSaTB09oX9rKrLHlBlogFJmuK+8Z/i07o2xbEKlcQ7ogMm01Kq+PjwFyn0tNhtxAPD3A0sztzJ0Wkl6MpEGda91tdn0WhqzEstxafFD3ib7rc8rQKGzoGwhzcPjObZsglsDmRwjNpHm1KlNo2mi8fKJ/N45SR2B7um4KNrCzeZuga9go8iVQ9xStautvOo8JeYgfZzzn9bcUbyPSTgeh29bh5u7wD+QFQpREpj9xnboeIUGGYvcKZcCVVXDpBAsZgKysM+tkelHI4ooaQxmRrDw/PlEwgrDVMVdSn1cl/MlGIWV7t4jangr88VsPY1H0cefYDFF4ZIyapGXKNQ+igwiqgLwfZQOk2+f9eMWMN3c7danjMKIqbG1c+extYCD/9wjeOCvM0ckbaXCUnVbAlkxNjldVGsqM3nhfJxvHFgrL3Q2iLtcn0kZIShonWBawU5IbSJrXLlt0P8xel2ola7gVciXDV8HbNSytgdTOXJ0kl8E8jq1T074qi0fe2HANY/Ab5z+q3tgxFnJN9D9pdU84M5s9m23pv47JKqDjPwGgBa0kJIOjvuaaaC58vG8esdc6kIewmaWp8WNTGUMMZbzXeyi2g0NEKmlYuxIKmOGSmV3DTqS87NKaI64u60zwaqT+O1o2uwcE4Z65b7efy3+Vx+tJuKDaejjP1I5oMgGdxdMr/5/AWp+zg3pwivZpKsR0hxRUhzh7h/yVuoD7Ko+OcILnp2CZ+WjuCewo/50bAN5LkamgtZNJhu/rj3UF6unGB7WMUqXRFBX1ADnlaumzroUxraKO72+i76nNGeGjL0xjZtdRdB8er0pZybU8QkfzXHZxTz0MT3OTJtb6/u21mbRpzIYIB2Kqd8q3GUfA/JKciioUG49jSrEHHCFX2oJeGSlnEX+H/S5pS7imfxx72H8lbVGM5YfwaXbl7IBRtPZmegcxNPTGpdG9M2a9Qb1ujVJYoJ/lom+mrQxURQeDSzeVHVrxtM9VfyyL6pVEY6fjgWB5MJmv379eyo/WEjrfJ5wYBOVYXOk3d7UHX3I64JSN4H6J6ZNCnIs3O2tUnMpgkke8NMG7kfwhp79mdy494FnLJ+CQ/tO5TSiL975eg00ObUgN+wAoAyQ+hHViEZbU1Qnc1+0vQgvx//AbVG71PiKuCzmmHNi+m6gE8z+GXBV7RJudH6C9RDPjowvP2ZoP+CXt9/qNGrX5GI/LuI7BGRVfbfaVHHbhaRrSKySURO6b2og4u0rFSOO28Bmu7ls2WDIAOdp8VF1jAM/lA8jMf3Teb1ytE0mjpl4SReqxxDo2mZCRRCUWMGO0Op3L47rnttM0rB1VuPZdmBkWwNpFIbcWEqaDR1lBL8dgbEaE8gt9aOx4xucE7OdrJcrSo7uReD7zLAUjw37ViA0c7Xs68eqB0pw+g2jIjGp2+mQeO79nVebpxxdfNxXzsFT5SCJDv9rzauvQIdXZdVyw3jXlTOCzc8ifvYKqSHxcLPzNrB9mBqH2U9Em7bNZfaSGwgUpYrSKarVem/PjL+1ygvL351SNvvgWsqWrKj5FvTFzb5+5RS90TvEJGpwPnANGAEsFxEJinVeRXNg4nrH7kSX5oPpQbOoyUukobmOxWAulCARe/ejqFMhGkkaQb37jmcK/PX4RaDUBvvDomtlhTv9gL3j/8Qj6iY6kg+LX65vpY7t6XJPNTmOnMT4r8M1fgUqBBZriDXFR3DfxV+SrIWRhOFBuwPJZHnacDbR+sg7clfVhI7yvX5TZCWXOU+t5cjcybxSflmlh0YxQx/RZu4BU1XrN07zHqR3HFfdRWF8JNtxzPSU0dxKIWemFtEFDduP6qdEoXdRxfFJ7X5nJK5O0pOaDD6LwL1rreOodx9HFfP3QhmI/gvQPOd1vmF30L6a+F1CfCMUioIbBeRrcA84NN+ai8heLxufvqHywhVVkPwfxIkRTrktviSX77iYQzbLqnQCJgaoHiydDIRFb/uaIarsXlRLt5ip1LEFAERga2BNJ4qm4SOyc8LVrWbz7w1QVOP7+ViHgDXDNCGg7GDH+Vv5Pqiozlr/elM8FnJzoqDyZyUWcyto79se30f0hgQnv1DXvNrr8/kzB9Vgf/imPPun3MJX1ds48avH+f0rJ1M8lXh1yOETcFA4z+LZxNZVAVvpkG5C3KCcSKmFF7RSHL5qA43tDnWVokL5REfnl4EQzxXNoFQnEIfPUUBZpSNPGhqLK8qaI7U7Q+0ZJMLjroSLTml39oYKvTFo/waEVkjIn8RkaY0cCOB3VHnFNv72iAiV4jIShFZWVbWeZ6TwYgr46cJdEGrQcya5ldF9fvjnCOUhX2M8NTjou1k6qrh64io+Ao+Hp/VDOOyzQt5o3I0H9WMiHuOUlAV8VAd8VBnuKg3XARNjVV12Yz0tlZmgHs2IoJkPYahT2W0N8SvRq0l29XIjsZUdgdTOCNrJzcWdJ4moacYyvLlX/pyLu8vzcCXYuDxmhx1ai1Lrp6NJF8CQMQ0eKV4JVeueIRHt73LL6ady76kB7hj9zyWVozhmbKJXLTpJN6pHgUa6KfWMHNeNhluywUzqpfwieK1E37FX464khSX5SvvFgOvRPjFyK94/pDXOULfj7HRh7kzCWXr9hAuu4B2940ubWdzvSNk6sxOKaXO/ow/q8nnzl2z+rSNGBScsGQE2Y6C7xKdPs5FZDmQH+fQLcBDwG1Y37TbgN8Bl3ZHAKXUw8DDYOWu6c61gwVNc2N6zoLQKwloXUHwA3CN7fAsA43TR53N33a+x4FwU7ymcElBEosySzu8NqY1Bb/ZNafZBfBAJInlB0ZxYmZxTLGLiBJu3L6ADYEs5iTvJ0WP4NfC3NgUrRuDDun/AcDSvXt4cNNMGg0rTP2M4TO5POPX+PUIni7OFnpKZdjL9duO5orFG7h7/s8p27mLCYdqjJg0H3GNBsBUJj/78nHWVO2k0bB83tdV7SYvKY2d9SNYXhX70Gt6aK6uLQYgXQ+jlEaWR+eCUVNZUnghmqaT6knm7RP/lWdW/ISCzLXMTClvXsy985BPuGZlFquK8mF9MvoxVUiqEdcTp2u055nSM59VA43vbzqZMd5aSsN+ysI+Kw1DqRvJDENS97JlxptJxrjCavCDiU50a1fpVMkrpU7qyo1E5BFgqf1yDxCd97PA3jdk0bLuwdy3HLBGqQMZDatIav7ZjvHnsLOhPO55FxYu5KIJi9jTUEFZsI5paSNx6y7M0Peg8qyO27Dfz/bGVCqjojMB7tg9m4qIl/NyiqxMio3p3FM8kzV2zpTP6poUn+LLulwemfQeRY0ZrKnPJtuby4ljbyJdz+Pjsk3cveEVGs2WgKFX967m6iyzjYI3IqDZA9K+6ucsd5AnJ7+NaOlohyyABW1Lya0o38raql3NCh4gYITYVR+/z1tTbVi+7uGgh8Vjzkez34Qy62kMBVgy8r3mxdomktwGPz5+JVc9cRYYCuPLVFzHdy1quFsE7emcR1B24d2u9m2d4WF9gxUgaJa6MT9PQ/JCSH47eeDjoeyog+jfjmr7SJqdWchhWWO6eFOHXhnmRGS4UqrJIfY7wDp7+xXgKRG5F2vhdSLweW/aOijIehoqzwO68cXuC1wto8eH5l7GGe//FrPVNP7y8QvR7dSUI/3ZjPS3ROxqnkMwcaFUJK7cIUNDNIUo+LQmelKnSNPDNJgu/nvvoTy8byqm0jHbL33CnnAqS9afTqreyHBvI6IUf97zR+6adQV/3vpejIIHaDTDvFY5mvNytsXItuz5TJY/n8FVt5UwemIQl7v3yr7ZGyjzz+2e83nFVgJGqM3+7k5BAyrE4rdvJ9WtUxoKoKFYnL6Tm0fH900Yk91UkESgxoUKCuJRVst98WUzFdrKerSQIliYC3UutCn1KL17t1dhwfw8DQwNGRFsuwQR75qmt1Hp4c753+PBtW9RopeimzqnZcxm5Og0Xt3zFS7R+P7Yo1kyam6P3+a3kd6uvtwlIodjfcd3AD8GUEqtF5HngA1Y6bJ+MtQ8a+Kheaaghq1E1f8N6u7HSqrR33gRs8XckuNL44NF/8Yd615iZeU2srwp/Ov0c5mYNrzj26T/Dqm+rp3psnDe16dyav4O9oQsd9Fj0vbw84JVZLqCmAhLK8Zwf8nhHSj4JoRD/JVsDmSyNeDFVIImijvXPEBpJL6Mj+2fydnZ23FHZbU88dwqlj2bxQ1nTyRQr3PCdyq58Q+7O3WL7FRh5XyG5mo/WjPTk4xHcxEye58FLqBCBEIAgomwvGYUP2cV7lbrJqaCIjMVbUEV5voUqNWt4W2bN9OL6FUB86gUK4Haaheq0o3K8CC5YZRbQUjAqzpV2mp/lFeS3rU+l6Cgv5PPHZeeygkTJ7BwYtsEa5eOP6EHb8oBeqnklVI/7ODY7cDtvbn/wYiID0m5DNN/AVRdD6GP6E1ayE5/JKKBa2LMLo/u4d8P+2632tF8p2K6D0PKFwOxYfJ/fP9I9q4ayePzUiDZ4NDUcm4b+3mMDf6MzJ149uv85455aAWt/KOjSNeCbG3MaM6dD4CCnaE0Jnj2URXJbDMqDuFDy/sCqv8FwiuAIG6P4q4Xivji7TS++iCFzLwIkbBVoCUeSkG1kUSGezio7fFP0qd1qOD3NFSSpPc+gKiF2A82pFw8WTqZi/I2xbhjBpXOI6XTkNww+jEHML5OtUfxseiYKKRnrpFN9VQB/fD6ltG1ZqU5JqShAkCa0VxnNS5Gy3tSJV4kv/OBzlmZR/DT/1pEWnJSp+c6dB8nd00/oWnJkPUwYNlbVeWFENnQ7ft0PArygGsq4p7RMyFboblGQP4azMAyqP8joEPKDRw5P5+nV7yE8V4m+Ax+dOlHeCR2tJnkMjhl8jbue28B9ak6Wnr8idsh/gOsbWib3K3R1PGoCF7NRdCMNCv6JN3N1RNPxu1Kg+xHUSqEKj8TjO3oOhxxcg1HnFwTc6/WQTLFQT//s/dQTin8BccNm4FZ+yzU/5oYI4s2ArL/Gldm0zS5efXTfFj6DS7ROrTNmA0CYQ3xG1ZSsW7G/zy2fwo1EQ8XD9tEhivI1kA6D5YcyoaGLMvFVQP98Nq41xroCCbRI/omZa3qdNR+N9roIOLt3Lgk0nwLxAUq2UBt8kNDGEa2b46UvBAoy+tFFXthWh3Kq9qt6nTe6CP4xdQzO5XHoec4laEGEHPfbCD+D7T7uMB3PpL6c0Tzd356L1lfUsId/3yLHXsP8MyFf2Vkatv3URd0c9nmE9geTmt3Wn9kagmr6nNpMNsGysz1lPLTwy/ioW3bWF9dTF5SGv9//EIW5k+POU+pCCrwKjQ8aoeVng/eoxDXMBAfKvQBn+//kAe21bKt0cXwpAx+NuV0jh8WW1jCDG+G0BfgmYnmjj1WGw6wu6GCkBHmys8faV3wr12UwipkHRZIsn5bPTGZW2nPuo6K0Jypsqk9oygJtc0PEYGQZqVDcJvoJxxoV9F3NHM0q3XEZ8adRURjbPKhtiRb/ZBkos2paY7OFbH8ti8dv5BThh/GmJTcbrxLh/boqDKUo+QHEDO8GSrOoT1bfdc9cjQk5zXENa4vxesyZtW/YAReRW9V+SkQ0Tll7ZmEOpjPj/JUUxZOjsnCCJCkRbghZz1nzXwZ6dAe0L+YyuTW1c/y9r61vQr779pn2YENvanxTu6hFBDQMN7NhNwg+py6ZhOL8UZOjPkEAE0h4xvQ7MRm3ZE9XmW+9q5XB1xWkRMDZGTI8rSxr1u28BbSPYMgFcgQoiMl7yQoG0A09yTIWwNpvwHfRZD5F8j9xMoTT1dHbi7IeChhCh5AUn6CSFJMBstAyMUT+yZ3qOABGkwPvx79BV6J4BYDQZEkEeZ4Szls+KwBUfAR0+BAqK45MrgJQ5lc9fmfWd5LBQ9dfVi3f5Lq+HDsiUpZo/W9SdYMAqDGBXHKL2IKqtQDjVqXslU2N2OCub/rn42WFUE/rA59Vh3asFDMPX+77uUu38eh9zg2+QFG0zTwnx+zT2U+iKo8v0s51sn9Ak1P7ChIXOMxMh/ni83XMSO1gso6H//78Uxey8pDUts3bLgwOCa9hIWZe5ieXMlbB0axtiaLEZ563qkdSU7Guf0qt1KKR7e+zRPbPyCiTFyic8WEhfxw3HHURRq56OM/UByo7FcZukpXTTyigfKADAuh9nsxv05Fm1ODcpsQNx2vQnwmqlxHshTKH99e3nx2k01/WxJqfQrq0BoYG+rwms5kX166jt+YBi4tQdXmv2U4Sn4QIJ5ZqJRboe4/OzoL0n+fcAXfxLqqEm4tmUft7hTUumRrsXFUAG1GPRLz27VMEkkSIUUPc3m+tfic5wmwKHM3/6wYy/v1Izkvr54U3+H9Jm9JfSXXffm/MYFihjL5/eY3+f3m3teRTSiaghQD9oPa78X4IBNtQj2kRKC6VVSsDjIuYEWi0gX3RgFztxdzvVV1yixKQR9T2ds09OyuL6cwdVjvbuLQJRwlP0jQUi7C9B4PFYtoY7hxzYCs55qjIwcDbs0qiaUXBFEjgxASCnzV7DFjS9ClaCEOTa5gXmopZ2TvIMWusRowdP6y7xDKQj6uGp3KxYf8e7/J+oOPHmRz3b5+u3/CMbHMM03U6phVbrQ5NZhfp0KV23oQKJDp9UhO14P1VARUddS9G6Rdu2JXbfYAD21Zxl2zftA1IRx6haPkBxGaezQq501UzW2W14f4IflHSPJliAweBQ8wNftYfNprNJgu60ftVVTh45ZRK1lfm8nHtcNxaybzUvfzz4qxHOHdjyhFyBSrLum+KZw+9npumXdEv8r56Ja3h7SCVybQoKPKmryVFLgU+qQGZo8Yy6qUHZgNYhUaTzUQHVSDoHzxzTTRi66WqUasBdTmEzQmekewJVgSM2NTJqgKF5IZ6VKU7OcVCU7P/S3CUfKDDHGNRbLaD6sfLLg0N7+beSbXfPUqprJSzYaVxsbgNK4eZ3KZEvZzFs+UVHDumBQWFt6CMoVlJa+Rnzqc6+ccNyByPrH9/QFpJ2EIGBuaXGitRC8yNsCYzGy+qrSDvvzKToVvmc5UjRshHF/RR5vyGzWMr1Ig3OKfccb8Kfx64SKu+PRh1lXvRhkCmsJV52H4Hi/lewIEDus8+M+tOapnoHBcKB16RSBSy8cl/6A6VMuc3CMZkz4z0SLFsOCNWzG67OV+kKEUxkY/altyrKukbiLT69HHxivwrVAGGJ+kox9tBZFFF4IpCOQxaWwOJjA/ewKL8w/nrS+2UFUX4KwFU8lJb0nvu6ehkm11pYzyZzE2JQ/V8BR7yh7gnI3HYznutT+cv6TwOK6ePOQKxiUMx0/eYUAIG0FW7H+F8kA507NmMSFzfucX9TMXfvR7ttT1X1HphKEUqsHEeCu3JR1nNH4D16K2nkJezcUVE09CK0/iDy98gjG1CtIi0KCxOHkuv1nS8+hTZVajyo6nPBjmjA1N94lKJ2lvT04dzuMLfmJ5mjn0CY6Sd+h3imvWceUXj1FnaJhKUMCRGQa3z70Tl9Y2unX1ge08suUdvLqbG6acwQh/+zljekNVYx0nv3dHv9w70aiwwng9N76rpK5wndE2/XGeN52lJ9wIQF0gyHtrigg0hlkwdQwFuR2XgeySTKFVqKprqAoFufyb+eyONC3EC5NS8rlhypnMzC7sdTsOsThK3qHf+eEH17O5wYuKiq8TTI5Og+sO/Tnvlq4nEAmxs7aUt8vWt7n+7IK5/Gr6d/pUpv0Hannqna9pMIP8w/MumrdPb59wlAJjWRYE2o7ktaww2jFtc87fMu07/Z6qVykTIpsBK3meJK5s2reGjpS8s/oxBJn3xq+IjoufnzqG3x/1435rb1/9FrYHPDEKHqwasx/WKD786Hd05lj9UvEX/HDssYxKaZu8rCfc/dy7PP3uqqg9uWiH1cHYQJ/cfzAgAtqMOswv06Js8gpEcePi4/jvxjeoN1oygp5TMG9AcrGLaOA+pN/bcegajpIfYrRW8KBYUbuDaz/+n35T9GGjEa3dRABdT7V1z8Z/8sDcS3otz7rt+1opeIvI6mS0rCBa2tBZiNWGh+CIKsxvkqFOh9QI2uR6vNtqePfif2N91W72Bao4MncSPtcQm8o4dAln5WMIcVSzgo/KE2v/X1G7s9/aHZkyrZP6q12brtcb8bxBus+jr3/W7jG1aXBEDPcl4jOtkXxYg0oP5qo0PmkoAWBaxihOHD7DUfDfYpyR/BAi3O6R7iau7R6/XvMcNUbvi2l8U7WHB795jdNHzmJ8arza8V2jIdh+Tww1lAnGRxnQGOWyWO/irQ3lvP3yLYhXIcCKxUNz8dmhc5yR/LeC/lPw/+/9e3lr35o+uVcIg7/u+IgLPn6Qm776Gz11Clhy5LT4BzSQQ6xC61bmRrtw9SByPuguar/HykDZerZkgmlHqiqazHgO30YcJT+EuG7MSfZWPKXV9x4Oqyq3szPQ1k2vL3indD0vF/fM0+q0eVMYm58Zu1NTUBhAS7UrVolYSn6vPeo/CJR9XPECGphxPltTg4ZYr5u6urr+EcxhUOMo+SHEhVMWEht80vQnfN4P0/XHtvVvyoBHt7zdo+tEhL//60X89OyjKchJJz3Viza/Gtf0+tgTkzQY7rYUftNfl4ju24FBGUC9ZuWIiWpWMiPx88brJpIda7Z6v/Kb/hXSYVDiKPkhxueL7+DWMd+nafE1GVe/KHjAqnfaj1SHG3p8raZpXHLKXF657VIWHlnYRuE1045i73hQL6TrQY5L30O63n7R8p6gVOxftCxKM1HNEw+7tGB6GLLCoEctfGsK/CYyPFa247Ict8ZvI71aeBWRZ4HJ9ssMoEopdbiIjAU2ApvsY58ppa7sTVsOXeesKTM4a0rfFPfuiCsnLuLDsm/ocq26bjI6OadP7nPyIVN5ZeNH4GuluTuq0adAhUHaWU+uNrzcMfYzQqbOTTsWsKK27UKxAJNThlMZrqc0WNP2JnHEELFG7aoStNyWfR5dw/SDgWn3tuDRXOT70zn74nm8/P4Gtm2oRZkgBY1oEwNt6uympKTg8O2jV0peKfW9pm0R+R1QHXW4SCnVf1UgHBLOxLThzMksZEv1RqrNvnfR66sI2HmTR1PwQQHFI3Zbi68aEDLB3f5DSTQwG3RwG3GfA14x2NmYSrorxAW5W9oo+cMyxvDw/CsQEZRS/Gbt33m15OuWE1TUv6ZRuwkIqGIvkhUGTDyaiysnLuIHhcd0+B5/ML7leLxF1neOdhZev630SVoDseKWdwELlVJb7JH8UqXU9O7cx0lrcPChlGL+m7+iN6P4eA6edx52AQuH991sJGKY3PvuW7xcspJIUpiMap0qrQY1wh13NK8iYG70o01raDMiBoUbA00gojRGeOrZHYotlvLGCb8iyxs7cq4I1vJmyWrKgjVETJOwMhjpy2TpxlUU72hAN3UyvH7K80rxJmtElMmFY4/ixxMXdTs1QF1dHf/Y9yWL8g8jP6X3OWkcBjf9nrtGRI4F7m1qxFby64HNQA1wq1Lqw3auvQK4AmD06NGzd+7sv6Adh77nT5uX8Zdt79BTJb8obwa/nL6ED0o3UhNuYGZmIVPSRw5IvpOnPl7J/TtfREU54ohYCp5GDZJMq1yeAM1GEut/bAqHlgyLTTx2xFVMyxjVI7mqQw2UBWsY4cvE7wQxOXSBXuWuEZHlQLzIlFuUUk1l1y8Ano46thcYrZSqEJHZwEsiMk0p1cYwqZR6GHgYrJF8Z/I4DC7eL22bbKw7LCtdy+2eCzizYHYfSdR1zpt3OC8sX8+u/RUYuSG00Y0oj0KVuK0RfMyvw5pv5OoNlBqto2bbPpAK/D3PwZPu8ZPu8Xd+ooNDF+hUySulTurouIi4gHOA5l+pUioIBO3tL0WkCJgEOLaYIcb09NEU1e1PtBg9wuN28fgvz+eJZSt56oOvaPjKAyZIfrAdvzOxFXznswxHSTsMFvrCB+4k4BulVHHTDhHJFbsoqYiMAyYC2/qgLYdBxs3Tz6a/0yb0Jyk+L1efdRQf3n0Nf7r2PIZPSoLccAd6vHMFPzdrfJ/K6ODQG/pCyZ9PrKkG4FhgjYisAv4OXKmUalumxuGgRxONP829nI6U39S0gnaPTUjO6wepuo+IMO+Q0STPCaKPa+x6XFQrUnQv9825uG+Fc3DoBb1OUKaUuiTOvheAF3p7b4eDg1nZhXy++A72NRygJhxgUvqINuc8t/0T7tm0NGafX/fw1DE/Gygxu0ReUjo76st6dG22O5nXT7yljyVycOgdThZKhz4j359JPplxj3238Ei+W3gkr+/+mjXVO7l2win4k3wDLGHnXFR4LKsqdxBSkW5dNyerkPvn/KifpHJw6DlO+T8Hh1a8tPsL7vtmKUEj0hxfGo1lflLsqi9nTEouP518KjOznLqlDonDKf/n4NANzh41l9NHzmRXfQWZnmSSXV7eKFlFebCWE/OnMzZlcKwjODh0BUfJOzjEwa25GJ86rPn1QNRGdXDoD5wslA4ODg5DGEfJOzg4OAxhHCXv4ODgMIRxlLyDg4PDEMZR8g4ODg5DmEHlJy8iZUBPcg3nAP1TUbr3DFbZBqtcMHhlGynGmrwAAAWTSURBVKxygSNbTxisckH3ZRujlMqNd2BQKfmeIiIr2wsESDSDVbbBKhcMXtkGq1zgyNYTBqtc0LeyOeYaBwcHhyGMo+QdHBwchjBDRck/nGgBOmCwyjZY5YLBK9tglQsc2XrCYJUL+lC2IWGTd3BwcHCIz1AZyTs4ODg4xMFR8g4ODg5DmINayYvI4SLymYisEpGVIjLP3i8i8qCIbBWRNSIyKwGyXSsi34jIehG5K2r/zbZcm0TklIGWK0qOG0REiUiO/Xow9Nnddp+tEZF/iEhG1LGE9puILLbb3ioiNw10+1FyjBKRd0Vkg/3dus7enyUiy0Rki/0/fvWWgZFRF5GvRWSp/bpQRFbYffesiHgSJFeGiPzd/o5tFJEFg6HfROR6+7NcJyJPi0hSn/aZUuqg/QPeAk61t08D3ovafh2r8OgRwIoBlusEYDngtV/n2f+nAqsBL1AIFAF6AvptFPAmVuBZzmDoM1uGkwGXvf1b4LeDod8A3W5zHOCxZZk60P1jyzIcmGVvpwKb7f65C7jJ3n9TU98lSMZ/AZ4CltqvnwPOt7f/BFyVILkeBy6ztz1ARqL7DRgJbAd8UX11SV/22UE9kgcUkGZvpwMl9vYS4All8RmQISLDB1Cuq4A7lVJBAKVUaZRczyilgkqp7cBWYN4AytXEfcAvIabsUaL7DKXUW0o11937DGiqAJ7ofpsHbFVKbVNKhYBnbJkGHKXUXqXUV/Z2LbARS1EswVJi2P/PToR8IlIAnA48ar8WYCHw90TKJiLpwLHAnwGUUiGlVBWDo99cgE9EXIAf2Esf9tnBruR/BtwtIruBe4Cb7f0jgd1R5xXb+waKScAx9nTrfRFpqjiRaLkQkSXAHqXU6laHEi5bKy7FmllA4mVLdPtxEZGxwExgBTBMKbXXPrQPGNbOZf3N/VgDCNN+nQ1URT28E9V3hUAZ8JhtSnpURJJJcL8ppfZg6a5dWMq9GviSPuyzQV8ZSkSWA/lxDt0CnAhcr5R6QUS+i/WUPmkQyOUCsrDMHnOB50Rk3EDI1QXZfoVlFkkIHcmmlHrZPucWIAL8bSBlO5gQkRTgBeBnSqkaa8BsoZRSIjLgvtEicgZQqpT6UkSOH+j2O8EFzAKuVUqtEJEHsMwzzSSi3+w1gCVYD6Eq4HlgcV+2MeiVvFKqXaUtIk8A19kvn8eeIgJ7sOzOTRTY+wZKrquAF5VlUPtcREyshEP9LldHsonIDKwv02pbKRQAX9kL1gmVLUrGS4AzgBPt/mOgZOuARLcfg4i4sRT835RSL9q794vIcKXUXtvMVtr+HfqNo4CzROQ0IAnLlPoAlunPZY9ME9V3xUCxUmqF/frvWEo+0f12ErBdKVUGICIvYvVjn/XZwW6uKQGOs7cXAlvs7VeAi2yPkSOA6qgp2UDwEtbiKyIyCWuRp9yW63wR8YpIITAR+HyghFJKrVVK5SmlxiqlxmJ98WcppfaR+D5DRBZjTfXPUko1RB1KaL8BXwATbY8HD3C+LdOAY9u4/wxsVErdG3XoFeBie/ti4OWBlk0pdbNSqsD+bp0PvKOUuhB4FzgvwbLtA3aLyGR714nABhLfb7uAI0TEb3+2TXL1XZ8N5EpyX/8BR2PZr1Zj2SVn2/sF+COWR8RaYM4Ay+UB/gqsA74CFkYdu8WWaxO2Z1AC+28HLd41Ce0zW4atWLbvVfbfnwZLv2F5H222ZbglgZ/Z0VgL5mui+uk0LNv321gDneVAVoK/W8fT4l0zDuuhvBVrxu1NkEyHAyvtvnsJyBwM/Qb8B/CNrS+exPIi67M+c9IaODg4OAxhDnZzjYODg4NDBzhK3sHBwWEI4yh5BwcHhyGMo+QdHBwchjCOkndwcHAYwjhK3sHBwWEI4yh5BwcHhyHM/wFFiVmt4baVpgAAAABJRU5ErkJggg==\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ }
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "import matplotlib.pyplot as plt\n",
+ "from sklearn.manifold import TSNE\n",
+ "def plot_tsne(labels,output):\n",
+ " tsne=TSNE().fit_transform(outputs)\n",
+ " plt.title('tsne result')\n",
+ " plt.scatter(tsne[:,0],tsne[:,1],marker='o',c=labels)\n",
+ " plt.savefig(\"GCS_tsne.png\")"
+ ],
+ "metadata": {
+ "id": "GCA-iK6PIxtg"
+ },
+ "execution_count": 28,
+ "outputs": []
+ }
+ ]
+}
diff --git a/recognition/MySolution/s47539934-GCN/GCN_tsne_100.png b/recognition/MySolution/s47539934-GCN/GCN_tsne_100.png
new file mode 100644
index 0000000000..c2903796eb
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/GCN_tsne_100.png differ
diff --git a/recognition/MySolution/s47539934-GCN/GCN_tsne_200.png b/recognition/MySolution/s47539934-GCN/GCN_tsne_200.png
new file mode 100644
index 0000000000..c793327c14
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/GCN_tsne_200.png differ
diff --git a/recognition/MySolution/s47539934-GCN/GCN_tsne_50.png b/recognition/MySolution/s47539934-GCN/GCN_tsne_50.png
new file mode 100644
index 0000000000..491855f840
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/GCN_tsne_50.png differ
diff --git a/recognition/MySolution/s47539934-GCN/Model.py b/recognition/MySolution/s47539934-GCN/Model.py
new file mode 100644
index 0000000000..c4827c3f22
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/Model.py
@@ -0,0 +1,81 @@
+"""
+Author: Arsh Upadhyaya, 47539934
+Code for 2 layer GCN model
+"""
+import math
+import torch.nn.init as init
+import numpy as np
+import scipy.sparse as sp
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from torch.nn.parameter import Parameter
+from torch.nn.modules.module import Module
+import torch.optim as optim
+from random import sample
+import matplotlib.pyplot as plt
+
+
+class GraphConvolution(Module):
+ '''
+ Starting of graph convolutional layer.
+ Parameters:
+ input_features: dimensions of input layer
+ output_features: dimenstions of output layer
+ use_bias: optional but good practice
+ '''
+
+ def __init__(self, in_features, out_features, use_bias=True):
+ super(GraphConvolution, self).__init__()
+ self.in_features = in_features
+ self.out_features = out_features
+ self.use_bias=use_bias
+ self.weight = Parameter(torch.FloatTensor(in_features, out_features))
+ if self.use_bias:
+ self.bias = Parameter(torch.FloatTensor(out_features))
+ else:
+ self.register_parameter('bias', None)
+ self.reset_parameters()
+ #initialize parameters
+ def reset_parameters(self):
+ self.weight = nn.init.kaiming_uniform_(self.weight)
+ if self.use_bias:
+ init.zeros_(self.bias)
+
+'''
+parameters:
+in_feature: an n-dimenstional vector
+adj_matrix: an adjacency matrix in tensor format
+'''
+ def forward(self, input, adj):
+
+ support = torch.mm(input, self.weight)
+ output = torch.sparse.mm(adj, support)
+
+ return output
+
+
+class GCN(nn.Module):
+ '''
+ A model that contains 2 layers of GCN , by creating 2 instances from GraphConvolution function
+ parameters:
+ in_feature:n dimensional vector, which is input
+ out_class: n dimensional vector, final output
+ in this case model goes 128->32->4
+ since in_feature=128(known from dataset)
+ out_class=4(since finally 4 classes)
+
+ '''
+ def __init__(self, in_feature, out_class, dropout):
+ super(GCN, self).__init__()
+
+ self.gcn_conv_1 = GraphConvolution(in_feature, 32)#32 is like the hidden layer for the overall model
+ self.gcn_conv_2 = GraphConvolution(32, out_class)
+ self.dropout = dropout
+
+ def forward(self, x, adj):
+ x = F.relu(self.gcn_conv_1(x, adj))
+ x = F.dropout(x, self.dropout, training=self.training)
+ x = self.gcn_conv_2(x, adj)
+
+ return F.log_softmax(x, dim=1)
diff --git a/recognition/MySolution/s47539934-GCN/README.md b/recognition/MySolution/s47539934-GCN/README.md
new file mode 100644
index 0000000000..dd92300640
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/README.md
@@ -0,0 +1,75 @@
+
+# GCN on Facebook.npz Dataset
+### By: Arsh Upadhyaya
+### roll_no: s4753993
+## Goal
+
+The objective is to accurately classify nodes into there respective categories(total 4)
+as per the facebook.npz dataset
+## Why GCN
+
+GCN and a conventional CNN are similar in there objectives, they both take some features
+from existing/given data and perform some operation on it, be it classification, recognition or even
+creation(like in GANs). However the difference lies in there flexibility. A CNN requires data in some
+clear format(like in images). However in a lot of real world applications, this is not the case. In fact,
+the internet itself is a graph with the websites themselves being the nodes and the edges being hyperlinks.
+Such is the case with the facebook dataset, and we have to classify the websites to certain classes.
+
+## Working of GCN
+
+GCN use graphs as objects, and to create these, they multiply features by features by weights. They use adjacency matrix to store data. This matrix is used in forward pass(function used in model) and thus forms a graph, in which adjacent nodes have information about each other. For a simple 2 layer convolutional network, like the one used in the model, each node has information of nodes within 2 edges. Hence one can Imagine just how strong a deep GCN can be, as unlike the neurons in CNN, the nodes in GCN are not bound by euclidean geometry. Especially on a bigger dataset(internet), it could be assumed there would be a lot of hyperbolic and elliptical non-euclidean connections over space, thus increasing the interconnectivity of the model.
+
+## Program Flow
+
+#load_data()
+this function is responsible for first extracting features,edges and targets, then create an adjacency matrix, and normalize that matrix.
+Further it returns features as a tensor.
+
+#GCN_model()
+Since the given data has input of first layer as 128 dim vectors, a hidden layer of 32 was used and then directly finished with out_class=4, which is the number of required categories. Alternatives, a third layer could have also been added, however the accuracy was already pretty good.
+Maybe a dropout was not necessary in hindsight as the dataset seems to small to need it.
+
+train_model()
+considered 200 epochs, and at each epoch, found difference between ouput of model and the target itself.
+Similarly for losses as well.
+Done for both training and validation set.
+
+
+## results
+### accuracy plot
+
"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 35
+ },
+ "id": "4Tpyn_NtoRSE",
+ "outputId": "927e952a-8a55-4448-b8f2-fbd1a0fb6b4d"
+ },
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "'\\nAuthor name: Arsh Upadhyaya\\nRoll no. s4753993\\nCode for 2 layer GCN\\n'"
+ ],
+ "application/vnd.google.colaboratory.intrinsic+json": {
+ "type": "string"
+ }
+ },
+ "metadata": {},
+ "execution_count": 1
+ }
+ ],
+ "source": [
+ "'''\n",
+ "Author name: Arsh Upadhyaya\n",
+ "Roll no. s4753993\n",
+ "Code for 2 layer GCN\n",
+ "'''"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "from google.colab import drive"
+ ],
+ "metadata": {
+ "id": "jsqqEDjjqjZi"
+ },
+ "execution_count": 2,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "drive.mount('/content/drive')"
+ ],
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "p_dNPCQKrVqa",
+ "outputId": "b49f52ea-d538-45b0-9ebf-de7ab4d024fe"
+ },
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Mounted at /content/drive\n"
+ ]
+ }
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "import math\n",
+ "import torch.nn.init as init\n",
+ "import numpy as np\n",
+ "import scipy.sparse as sp\n",
+ "import torch\n",
+ "import torch.nn as nn\n",
+ "import torch.nn.functional as F\n",
+ "from torch.nn.parameter import Parameter\n",
+ "from torch.nn.modules.module import Module\n",
+ "import torch.optim as optim\n",
+ "from random import sample\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "metadata": {
+ "id": "V2CFruE7r4yV"
+ },
+ "execution_count": 4,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def load_data(file_path):\n",
+ " \n",
+ " data = np.load(\"/content/drive/MyDrive/facebook.npz\")#path of file through google drive\n",
+ " edges = data['edges']\n",
+ " features = data['features']\n",
+ " labels = data['target']\n",
+ "\n",
+ " features = sp.csr_matrix(features)\n",
+ "\n",
+ " adj= sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),shape=(labels.shape[0], labels.shape[0]))\n",
+ "\n",
+ " #normalize\n",
+ " colsum = np.array(adj.sum(0))\n",
+ " D = np.power(colsum, -1)[0]\n",
+ " D[np.isinf(D)] = 0\n",
+ " D_inv = sp.diags(D)\n",
+ " adj_trans = D_inv.dot(adj)\n",
+ "\n",
+ " #transform data type\n",
+ " indices = torch.LongTensor(np.vstack((adj_trans.tocoo().row, adj_trans.tocoo().col)))\n",
+ " values = torch.FloatTensor(adj_trans.data)\n",
+ " shape = adj_trans.shape\n",
+ "\n",
+ " adj_trans = torch.sparse_coo_tensor(indices, values, shape)\n",
+ " features = torch.FloatTensor(np.array(features.todense()))\n",
+ " labels = torch.LongTensor(labels)\n",
+ "\n",
+ " return adj_trans, features, labels"
+ ],
+ "metadata": {
+ "id": "KDdp_bTnru0h"
+ },
+ "execution_count": 5,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "\n",
+ "\n",
+ "\n",
+ "class GraphConvolution(Module):\n",
+ " '''\n",
+ " Starting of graph convolutional layer.\n",
+ " Parameters:\n",
+ " input_features: dimensions of input layer\n",
+ " output_features: dimenstions of output layer\n",
+ " use_bias: optional but good practice\n",
+ " '''\n",
+ "\n",
+ " def __init__(self, in_features, out_features, use_bias=True):\n",
+ " super(GraphConvolution, self).__init__()\n",
+ " self.in_features = in_features\n",
+ " self.out_features = out_features\n",
+ " self.use_bias=use_bias\n",
+ " self.weight = Parameter(torch.FloatTensor(in_features, out_features))\n",
+ " if self.use_bias:\n",
+ " self.bias = Parameter(torch.FloatTensor(out_features))\n",
+ " else:\n",
+ " self.register_parameter('bias', None)\n",
+ " self.reset_parameters()\n",
+ " #initialize parameters \n",
+ " def reset_parameters(self):\n",
+ " self.weight = nn.init.kaiming_uniform_(self.weight)\n",
+ " if self.use_bias:\n",
+ " init.zeros_(self.bias)\n",
+ "\n",
+ "# parameters:\n",
+ "# in_feature: an n-dimenstional vector\n",
+ "# adj_matrix: an adjacency matrix in tensor format\n",
+ "\n",
+ " def forward(self, input, adj):\n",
+ "\n",
+ " support = torch.mm(input, self.weight) \n",
+ " output = torch.sparse.mm(adj, support)\n",
+ "\n",
+ " return output\n",
+ "\n",
+ "\n",
+ "class GCN(nn.Module):\n",
+ "\n",
+ "# A model that contains 2 layers of GCN , by creating 2 instances from GraphConvolution function\n",
+ "# parameters:\n",
+ "# in_feature:n dimensional vector, which is input\n",
+ "# out_class: n dimensional vector, final output\n",
+ "# in this case model goes 128->32->4\n",
+ "# since in_feature=128(known from dataset)\n",
+ "# out_class=4(since finally 4 classes)\n",
+ "\n",
+ " def __init__(self, in_feature, out_class, dropout):\n",
+ " super(GCN, self).__init__()\n",
+ "\n",
+ " self.gcn_conv_1 = GraphConvolution(in_feature, 32)#32 is like the hidden layer for the overall model\n",
+ " self.gcn_conv_2 = GraphConvolution(32, out_class)\n",
+ " self.dropout = dropout\n",
+ "\n",
+ " def forward(self, x, adj):\n",
+ " x = F.relu(self.gcn_conv_1(x, adj))\n",
+ " x = F.dropout(x, self.dropout, training=self.training)\n",
+ " x = self.gcn_conv_2(x, adj)\n",
+ "\n",
+ " return F.log_softmax(x, dim=1)"
+ ],
+ "metadata": {
+ "id": "dZwEJTIVt9-C"
+ },
+ "execution_count": 6,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def accuracy(output, labels):\n",
+ " '''\n",
+ " calculate accuracy\n",
+ " parameters: \n",
+ " output:result of running an instance of the model\n",
+ " labels: the true value\n",
+ " function compares ratio of two values, giving result<1, \n",
+ " as predicted probability always less than true value\n",
+ " '''\n",
+ " predict = output.argmax(1)\n",
+ " acc_ = torch.div(predict.eq(labels).sum(), labels.shape[0])\n",
+ " return acc_"
+ ],
+ "metadata": {
+ "id": "qsMqOqxTwjd9"
+ },
+ "execution_count": 7,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def loss(output,labels):\n",
+ "\n",
+ " prab = output.gather(1, labels.view(-1,1))\n",
+ " loss = -torch.mean(prab)\n",
+ " return loss"
+ ],
+ "metadata": {
+ "id": "WUessmBVwpQb"
+ },
+ "execution_count": 8,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def train_model(n_epochs):\n",
+ " '''\n",
+ " parameter: number of epochs\n",
+ " trains model over the range of the epoch and at each train, \n",
+ " calculates accuracy and losses\n",
+ " '''\n",
+ " train_losses=[]\n",
+ " validation_losses=[]\n",
+ " train_accuracies=[]\n",
+ " validation_accuracies=[]\n",
+ " for epoch in range(n_epochs):\n",
+ " model.train()\n",
+ " optimizer.zero_grad()\n",
+ " output=model(features,adj)\n",
+ " train_loss=loss(output[train_set],labels[train_set])\n",
+ " train_losses.append(train_loss.item())\n",
+ "\n",
+ " train_accuracy=accuracy(output[train_set],labels[train_set])\n",
+ " train_accuracies.append(train_accuracy.item())\n",
+ " train_loss.backward()\n",
+ " optimizer.step()\n",
+ " output=model(features,adj)\n",
+ " validation_loss=loss(output[val_set],labels[val_set])\n",
+ " validation_losses.append(validation_loss.item())\n",
+ " validation_accuracy=accuracy(output[val_set],labels[val_set])\n",
+ " validation_accuracies.append(validation_accuracy.item())\n",
+ " print('Epoch: {:04d}'.format(epoch + 1),\n",
+ " 'Train loss: {:.4f}'.format(train_loss.item()),\n",
+ " 'Train accuracy: {:.4f}'.format(train_accuracy.item()),\n",
+ " 'Validation loss: {:.4f}'.format(validation_loss.item()),\n",
+ " 'Validation accuracy: {:.4f}'.format(validation_accuracy.item()))\n",
+ " \n",
+ " np.save('train_losses', train_losses)\n",
+ " np.save('train_accuracies', train_accuracies)\n",
+ " np.save('validation_losses', validation_losses)\n",
+ " np.save('validation_accuracies', validation_accuracies)\n"
+ ],
+ "metadata": {
+ "id": "1tJrfwlHw2bC"
+ },
+ "execution_count": 9,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "def test_model():\n",
+ " output=model(features,adj)\n",
+ " test_loss=loss(output[test_set],labels[test_set])\n",
+ " test_accuracy=accuracy(output[test_set],labels[test_set])\n",
+ " print('Test set results:',\n",
+ " 'Test loss: {:.4f}'.format(test_loss.item()),\n",
+ " 'Test accuracy: {:.4f}'.format(test_accuracy.item()))"
+ ],
+ "metadata": {
+ "id": "dnk6qMppxA1h"
+ },
+ "execution_count": 10,
+ "outputs": []
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ " adj, features, labels = load_data('facebook.npz')#returns normalized adjacency matrix, tensor features and labels\n",
+ " features.shape[0]\n",
+ " num_nodes=features.shape[0]\n",
+ " #split data in semi supervised quatity, i.e train:set:test=20:20:60(since n_train"
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD4CAYAAAD8Zh1EAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3deXxU1fnH8c8hBMK+xsi+iQoBwhIRRRbFBVFBURQqVnBrUSou1aJYRW1/1dYqYt2oWtGiFFEULUJtWUQFJWwKwQUSlrCEJBAgsibz/P54ZshC9kwymZnn/XrNKzN37tx5cjP5zplzzz3jRARjjDHBr0agCzDGGOMfFujGGBMiLNCNMSZEWKAbY0yIsEA3xpgQUTNQT9y8eXNp3759oJ7eGGOC0urVq9NFJLqw+wIW6O3btychISFQT2+MMUHJObetqPusy8UYY0KEBboxxoQIC3RjjAkRFujGGBMiLNCNMSZEWKAbY0yIsEA3xpgQYYFujDF+tHQpzJsHgZiZ3ALdGBNQ33wDixZBdnagK1EHD8KYMfDSS+DxFL7O0aMwYQL89a/5g3vpUrjsMhg5Evr3h++/P/WxBw5AVlallB64M0WNMaHJ44EapWgqHjwIEyfC22/r7ZgYuPJKGD0aLr64+MeKwHffQceOUL8+pKZCgwZQt27u/Zs2wRdfQGQkDBwInTrp7QkToGlTaNYM9u6FnBw4/XS45hoN4YkTYeFCmD0b/vQn2L8fGjaEc86B11+H2rU1sP/7X32u1at1O6mpkJysz3P33fD730N8vP6MjYVPPoHPPoOkJN3OLbeUfx8Xs2MkIJc+ffqIMSZwliwRufVWkW+/zb983TqRc88VWbMmd9lf/iIyaZKIx1P8NrdtE2nbVmTKlMLvT0wUGTdOZM4ckfh4kZo1dd0PPhC57jqRhg1FQOSyy0T++1+RH34QeeklkdRUkcOHRcaPF7nqKpHevXW9rl1Fnn9epE4dkZgYkSefFJk+XeS88/T+vJfLLxdp0ECkfXu9v2tXkQsvFLn0UpE2bfKv++qrIm+8ITJypP7e48aJREWJxMaKdOokUqOGyD/+IXL33br+2WeLXHONyA03iGzdqr/rjh0iAwfmbrNOHV3nj38U+e678v7VRIAEKSJXLdCNqSL795cciBWVnCxy1lkabEU915EjIo89pqEE+nPqVF3f48kNoU6dRDIzRT7/XMQ5Xfb66yLPPCMyapQG54YNGuKvviry4Yci55yTG2CvvSbyy19qMPpqa9ky9/6oKJFPPslf27FjIs8+K9KkSf6AjY/XUAWRuDi9PXWqSOPGuuyCC0QGD85dv317DfoffxTZuFHkiSdEGjUS6dhRJCXl1H2SkyOSkKC/x/vvF77fPvtMa27XTmTZstzlBw4Uva89Hn2+xYt1PX+wQDcmwDZuFKldW2TChPz//FlZIkOHisyYIXL0qMiNN4pMnqzLRUQWLtQQmjlT5MQJbbHOmyfy3HMif/5z/pDIyREZNCg3qIcO1XDcuTN3nWXLNJBAn2vbNpGxY/X2ww+LvPyyXr/1Vm09n3WWSOvWIh06aGj6AvO0005tAfsu77wj0qWLXve9Edx4oz6mcWNt+c+bJ7JqVdH768gRkdmzRV54Qd8QfNv53e/yr/fjjyIvvihy/Lju1717RXbvFsnOPnWbWVm5+7W8duwQOXSoYtuoKAt0Y8rhxImi79uyRVufiYkaPgsXinz0kcjq1RouCxZoEK1dq0Fz/fW5gXflldrCfOYZkTvv1GURESKXXJK7Ttu2IosWaYs2MlKX1ax5anhee21uy/r3v89tRT/1lEiLFnq7Xj2R3/5W5E9/EqlVS+TMM7U7wycnR+Tmm3O32aWL/u5z5mirNyZGZOlSkaQk7Yp55RV9vqQkbYX/9a/6hvX557nb3bRJ69m+XWTMGN3uJZfo/iiP114Tuekm3bfhzgLdhJWcHA3Dr78u/P5jx0SWL8/fchXRlt2QISJvviny/fcaZPffX/g2fvGL3LD0Bafv4gtg32XQIP350EManHXqiHTvnnv/HXdoSxi0P/mLL7TLwBf0X3+trdAHHtDavvlGJD1dQxtEfvUrkREj9PpNN+X/BPDjjxr6vhZu//4iGRmF77Ply7XbZPv28uz1ovm6HYx/FBfoTu+vevHx8WLzoRt/++wzuOceSEzU20OG6BCxmjWhd29IS9PRCenpen/DhjoK4rrrICFBRyw4pyMuUlM1chcsgKFD4S9/gbfegqlT4YYb4KabYM8eXefuu3WkRGIirFoFF14IXbroyIbHHoOICNi6FZo0yR0F8uyz8OWXMGuWbufTT+HXv9b70tN1tMV558GkSYX/rh6P1j1vno68eOwxmDxZ6y/oyBHYuRM6dNBaTPByzq0WkfhC7ytNoDvnhgLPAxHAayLyVIH72wFvANHAPmCsiKQUt00L9PCUmqrh07hx0evMmKHjkkeM0OCsXVuX5+To4+vWhVdfhQ8+gEOH4NJL4bbb4JlnYOZMOPNMePRRHUL2xhvQti0cOwbr12voxsfDqFGQkqIhm5EBc+ZoQP7rXzr++MsvNcgnTdJhZu3a6TC4OnU0HGvV0u23bFny77xjh76pdOnil12Yj4jWU6dO4UFuQk9xgV5i1wga4luAjkAtYD3QtcA67wE3e69fBLxd0natyyV8zJmj3QaHDom0aqUH+dLT9b6dO7UrYs8evb1smXYz1KmjXQSDB2v/7NSpenAub1fG+eeLDBuW251Qq5YeNDt8uOw1bt2qXRki2n/sq2fzZpHbbxe56CI9wLh9u0ifPqcenDNVbNs2fQE8/nj5hw4tWKB9W599ln/51q16RPmDDwp/3KpVInfdVfZhK2+9JfLoo9q/VQFUpA8dOA9YlOf2Q8BDBdbZCLTxXnfAwZK2a4EefObNE/nDH0T27SvbY0CHjPkOvEVGar/ya69pwPuCe9067Y/u3FmHy82cmb8/+tJLdajcH/+o/cw+q1bpAb9t2/z9G4eRo0c12IoLG49Hd/yRI0Wvc/iwjkUsqSP+6NGi33kzMvQAwcaNp953/LgegW7TRt/5QQ8gXHWVjk0sOIzFd8S44PXXX899fK9eunzxYh1W4zsoUqeOtkbGjtXB6AsX6gvaN1h+6FAdsvPMMyLTpulYzpYt9UDI+++LPPKIvig9Hh0nmvegSQXGr1Y00K9Du1l8t28C/lZgnXeASd7rIwEBmhWyrTuABCChbdu25f6FTOXzeERWrNADiMePizz4YO7rsXFjbaEuWqQjHpKTNYDHjdOgHjVKD8YtXaoncvTqJdK0qT72F7/QA3u+oXWtW+eOznBOD0TmPdFl6VJthCUlBWpPlNOJE7rzSuvIEd1pIvrzwQc1PIv7xy/NR5HU1PzDdf75Tx1iU3AA+IQJ+kd4/vnCt+PxiNx3n65zzjka/tOm6bLf/17PlJkyJTfs6tfXcZVffKHhnVdWlp6hU6OGHg2++GKRK67QI9K//KW+CHxHhH/1Kw3211/XdRo10vtiYjRMH3hApG5dHboDIs2ba7jfe6/Ib36j6w0cqMOSzj1X3wiuvlpODrt54YXc674XeLt2+vv5Bs03bKhjTn33n3GGDvQvOOSoWbP82wF9viuu0Ovjx+s/DuibQDlVRaC3BD4A1qJ97SlA4+K2ay306mXfPs0RXwPt7bfl5BC2Xr30+q9/ra3ha6/NDWTQ0D7rLB1WN3Cg/s/5Wtbt2mlj7X//0/t8Dbf0dB1T/fPPevuBB7ShtXt3QH790klOFnn66ZLHzu3eracyRkfraY5bt+bu2Jdf1hbfzz/rqZq33679SW3byslhLnlPWxw8WMf6TZyoQXXLLfoY3x/lyiuLPu3wn//UP0psrMjcudrFEBmZG069euUffN6okZ458/33Wu/Ysfo7xMbmDsO5+moN67ynP/pauqDv5h9+mD/YunXTcYw+t9yi796TJumpmP366f467zwN0X79tLV81135P6KdcYb+7vPm5X8z873pLV+uA967dtWQr1lTW9GRkfqCrV1bX4Q1augb0YkTeuncWbf/m9/kH8S+dq22JtLTtXtlyRJ9I/R9RH31VX1D2L1bJC0t93Wxdq3W/803+gYTGalvfr5PCNOn61lm5VTpXS4F1q8PpJS0XQv0qvWf/+jp1G+/fWrDcc2a3BZ006b6/9K2rf4Pt2+vjZyC3YnbtumY47VrRQYM0FD/z3/0vp07tbX+5JO5gR0wHo+2FB9/PLel6vGI/PRTbhD88IOGmK8rYft2Pbtn8GA9X/yhh3T9s8/WnfToo7nbf+UVDYI33tCd8vHHutPq1tVg8oVRq1YaRr7b/fppwERF6e24uNyxhw0bajj97W+6Hd8g9O7dNfBOP13D7+679eNS3bq687/5Rt8Z8wbweefpKZ++5+3USQ8QPP+8ninkC+MzztADBk2b6rvw+PG6fORIvYwYoW9mvgHo8+aJ7Nqlt3fs0MBauTL/fv/pJ31Tad5c3wRWrNAQ9L1xlUZKirZmly4tezeFL5gXLNA3r8WL9XbBEwzWrhV5993KOY03JUVfW35U0UCvCSQBHfIcFI0tsE5zoIb3+h+BJ0rargV61cnI0FD2nZhy1VW67Lzz9Oy9Bg20UfjKKyI9e+b+76987Ts5fiS72C5TEf0/qFBwb9umAfrwwyIHDxa+ztKl2jravDl32bFj2n0wduypH+t9fIO1fa3dp57SdyDQgPryy9yjqtHRGkBt2+rO6ttXg8AXer6PIBERGl5ffaWPzdtCBT3q+/XXumO+/FJ37Pnn5+5838f8Xr30D5GZqS3inByRv/9dz07y2bBBzwrydccUtHt3/kHtNWtq63jUKA33o0d1Py1erHUU7Nvev1/D2bdfv/km91TS8eP9E3I7dugbScOG2jq+/PLiz9oyxapQoOvjGQb86B3tMsW77AlguPf6dcBP3nVeA2qXtE0LdP95/HH9Hyl4SvLDD2u3Xmys/p/7jt+AHveJjNRPqNdck9tHnZmpLfmnBn+qK150UW4/yIkT2rI7/XRt0eSVk6NhsHatfkTNzCw8DFJTtRX78svaLzpmjAZiRISGY7t2GpQ+Ho+2kPMG5vXX65vAK6/kLuvaVQPy1lu1X2jKFF0G+hyvv57bVdCihb4R1Kmjfa9t2ugIBN/56o0a5Q/VTZu08//ttzUA27TRM4rattXrmZna7fHsszpjU2FdMh6PHvX13ff110W/eZVVRoYegHvzzbIdsS7Kvn36xlLSO3lZbNminy4uuKAafGwLbhUO9Mq4WKCX3YIF+ok1bw74GomgQ/h83SkzZsjJ41fNm+soEBHNlVvGHJY+rJJ//MO7kcREbUkuWaJh6PFoX2mjRhp6rVppC9l3ymP9+tqa9YXHvHmnni4J2k/pc+iQHjzzjUf0XRo21NMxt23TGjp21Heav/1N30B83RS3366t4kce0TBt1Uov/fqJzJqlfbAXX6xjF0FbgkOGaFeAb6f4PkpkZ2tL1Rfw8+fr/QcP6ptHcZOMiGiLc8gQfey//13+P2i4OXy48ElWTJlYoAeh3bu1Ydm6tZ7OnZiY291av74eOL/3Xu36bNMmt+UdHZ3bbTJ8SJacWLJcW27vvntyMHjOoMG6wqJFuR//817uv19bzA8+mDuWEDQs33xTl9WooV0dX32lfbg9e2p3xZw5GqLDhmkwb9miszX5tnHDDTryISVFPxYUHGaWkaEHsnwjGUA/auRt7a9fn3vfokX5H79li74ZJCeXvJM//FDHQJZHTo7/z5E3phQs0IPEwYMi772nWTFunOanL9saNNDjXx9/rMNYzz5bgz3mNM/J8yIWLtTjV4POPSI/xl0rHl9rNe8lKkqb9M2ba3dDgwbarbJwobbQr702d11fv+3WrRreX36ZW+zkybnrtWhx6vCUlBR9Lt+kJH375u9KKY7Ho10XnTrpm0NhkpK0C6Sy56M1ppqxQK+mCmbRpEn6F7n1Vm0gT5qky3XoqkdWj/qTnjzhGwK3cKF2WYwdq+8EDz2kHeW+8cJ3360HEn/4QQ+uvfOOyOjRGoS+M35q1cp/wC0rS8frDh9ecvFffqnjl4vqovANXr/zTjsIZoyfFBfoNjlXgBw97GHl6VeTdsU4Rr07koMHoXVrbfJmZUFcrU2svPAhojatRTp35lCbWBq+OV0ffO21+n1YU6fq5CS7d+tkJaAzTWVn6yxPL71UdAEiOotVjx5w662n3peTozNaVUR2NqxbB3362EQjxvhJhSfnqgzhHugL/7SWoQ/3ZgX9yPrPCr7/Xmfs+3rONj7+2zYmrxlFvVrZ+uWKixfr9Htjx0L37jqlngjExen0gkePwvbt+mWG99yjs0ktWQL16gX61zTG+FlxgW5fEh0gO15bCMB5rKTz5clsdR34e6up9L3+cfoCtGgBSz6Hs86CzEyd83XECG2B33qrBnqTJrlzobZpoz9nzw7I72OMCTwL9Kr2zTdsiYqlc9IiDjZsTcODKTx/3my2N+vFbR89rvO6Xn01DB6cOzdr48Y68bVPs2YBKd0YU71ZoFeGI0fgmWfw3Dyeo01bUveDf/J99ACOfracns/dzKEmg+nPlxy96bew9nOGbfgzHD6s/dkzZ+rk1sYYU0YW6JXhz3+GqVP59k8L+OToJTwiT9KOKCLIYQsd6bl/KQCR110G53XTb1H41a+0b9zC3BhTThbo/vLjjzBsGFx/PZ7npvEDZ9PzyEp6spKl0aOIjnG0OL6N/4v9lEePPky7tR/C+efrV9/ceGOgqzfGhAAb5eIvkybBdB1WeLxGbfo2+J4VN71IncQ18PHH+r1pPiJw/Hjud6sZY0wpFTfKpUZVFxMycnLY8fBLbGp4Lkn//Eq/PXjMGL79v0+4xvM+N/2+PXVe+Av873/5wxx0TLaFuTHGz6zLpTxE8Fw5nDYLF3CMWtT45WCQE0zZ/iuenjOIFq1h7p2BLtIYE26shV4eM2dSY+ECHuRppt+8hiypxybO5tVNA7n/fli+3I5tGmOqnrXQS8HjgdRUPdeH9HSOTPwtq+nPvvG/5c9v1GBmp/Xs3Qubn3Q0bhzoao0x4coCvRReew3uvBO++goaTnuJs3/O4F+DX+HlV/UDzs2/bxvgCo0xxrpcSmXWLJ2rasIdOdT/12t81eBSnlnYjcjIQFdmjDG5rIVegt27oeHnn7Cw6Sw+XX8urdlB9mPP2SAVY0y1Y4FelD17YOZMDr6/gY/5J+yDy5jN4YYxtL97eKCrM8aYU1igF2bPHhg4EH76iVYRDZnVZCI3JtwLU6ZQ9+KLsb4WY0x1ZIFe0JYtcNVVyK5dPHzBcp764gKmPw50BN59N9DVGWNMkSzQ81qxAq64gmPHYUztf/PRVxcwfTr85jeBLswYY0pmge5z6BCMGcPPtZvQff9nxHTvyFfT4NxzA12YMcaUTqmGLTrnhjrnfnDObXbOTS7k/rbOuSXOubXOuW+dc8P8X2ol+93vkO3bue7w2zTq2ZGlSy3MjTHBpcRAd85FAC8ClwNdgTHOua4FVnsEmCMivYDRQDHfTlwNJSXByy+zOPZulh4/n9mzbe4sY0zwKU0LvS+wWUSSROQ4MBsYUWAdARp6rzcCdvmvxCrw5puIc/xm6/1cf71+jacxxgSb0gR6K2BHntsp3mV5TQXGOudSgAVA8BxG9Hhg5kx2d7uETVltGD8+0AUZY0z5+OvU/zHAmyLSGhgGvO2cO2Xbzrk7nHMJzrmEtLQ0Pz11BS1cCNu384ZnPB066PBzY4wJRqUJ9J1Amzy3W3uX5XUrMAdARFYAUUDzghsSkRkiEi8i8dHR0eWr2F+OHdOvjLviCrKbncYfN17N+PFQw2a3McYEqdLE1yqgs3Oug3OuFnrQc36BdbYDQwCcc13QQK8mTfAirF4Nn34KEydy93kJ1KwfxZ32pRTGmCBWYqCLSDYwEVgEbEJHs2x0zj3hnPNNanI/cLtzbj3wLjBOAvVlpaW1ejUAm0ZM5pV/t2HSJGjWLMA1GWNMBZTqxCIRWYAe7My77NE81xOB/v4trZKtXg0xMUyf25J69eC++wJdkDHGVEz49hivWQO9e7NkqWPwYGjaNNAFGWNMxYRnoB85AomJZJ3dhx9+sJEtxpjQEJ6Bvn495OSwPqIPAIMGBbgeY4zxg/AM9DVrAFiY1od69aBXrwDXY4wxfhBesy3u2we33w6ffQbR0cxf05rzz7fvqzDGhIbwaaF7PHDzzfDxxzB6NLun/YvvNjjrPzfGhIzwaaFPnw6ffAIvvIDcNZHxl0O9eprxxhgTCsIn0F9/HS64AO66i3fegUWL4IUXoE2bkh9qjDHBIDy6XNLTYcMGuPxycI5p06BHD5gwIdCFGWOM/4RHoC9frj8HDSI5GRISYOxYiIgIbFnGGONP4RHoS5dCnTpwzjnMnauLrrsuoBUZY4zfhUegL1sG550HtWrx3nsQHw8dOgS6KGOM8a/QD/T9++Hbb2HQIHbsgFWrrHVujAlNoR/oq1aBCPTvz7JluujyywNbkjHGVIbQD/RNm/Rnt2588QU0agSxsYEtyRhjKkN4BHqTJnDaaSxfDuefb6NbjDGhKTwCvUsXMvY5EhP13CJjjAlFYRPoX32lNwcMCGw5xhhTWUI70NPTIS0NunZl+XKoVQvOOSfQRRljTOUI7UD3HRDt0oWVK6F3b4iKCmxJxhhTWcIi0D1ndWHdOg10Y4wJVaEf6HXrkpTdlkOH7JuJjDGhLbQD/fvv4ayzWLtef82ePQNcjzHGVKLQDvSUFGjblrVrdex5t26BLsgYYypPqQLdOTfUOfeDc26zc25yIfc/55xb57386JzL9H+p5ZCaCjExrFsHXbvaAVFjTGgr8RuLnHMRwIvAJUAKsMo5N19EEn3riMi9edb/DRD43ursbB22GBPD2vlw6aWBLsgYYypXaVrofYHNIpIkIseB2cCIYtYfA7zrj+IqJD0dRDhQ93T27LEDosaY0FeaQG8F7MhzO8W77BTOuXZAB2BxEfff4ZxLcM4lpKWllbXWsklNBWBpYgxgp/wbY0Kfvw+KjgbmikhOYXeKyAwRiReR+OjoaD8/dQHeQH/1wxiGDtUvtTDGmFBWYh86sBNok+d2a++ywowG7qpoUX7hDfSfDsUw5/8CXIsxxlSB0rTQVwGdnXMdnHO10NCeX3Al59zZQBNghX9LLCdvoJ95QYz1nxtjwkKJgS4i2cBEYBGwCZgjIhudc08454bnWXU0MFtEpHJKLaM9ezhKFKd1ahDoSowxpkqUpssFEVkALCiw7NECt6f6r6yKkz2p7CGGFi1doEsxxpgqEbJnip7YmUoqMZx+eqArMcaYqhGygZ6zSwO9RYtAV2KMMVUjZAO9Rpq10I0x4SU0Az0nh8jMNGuhG2PCSmgGekYGNcRjLXRjTFgJzUD3jkE/UDuG+vUDXIsxxlSR0Az0LVsAyI625rkxJnyEZqBPm0Z6rRbsbdc30JUYY0yVKdWJRUFl2TJYtoxXT5tGs1b2jRbGmPARei30v/wFYmKYfuQOOyBqjAkroRfoCQlkD72SvYfq2JBFY0xYCa1A//lnSE3lYPOOANZCN8aEldAK9K1bAUir3wHAWujGmLASWoGelATAtpraQm9V6BflGWNMaAqtQE9OBmDjz9pC79gxkMUYY0zVCq1AT0qCevXYkBpNixZQt26gCzLGmKoTWoGenAwdOpCU7Kx1bowJO6EV6ElJ0LEjW7ZYd4sxJvyETqCLQHIy2e06kpICnToFuiBjjKlaoRPoaWnw889kNOiAiLXQjTHhJ3QC3TvCZUekJrkFujEm3IROoHtPKvrpRHvAAt0YE35CJ9D37gUgMSOGOnXstH9jTPgpVaA754Y6535wzm12zk0uYp3rnXOJzrmNzrl3/FtmKezdC86xcXdTOnYE56q8AmOMCagS50N3zkUALwKXACnAKufcfBFJzLNOZ+AhoL+I7HfOnVZZBRcpLQ2aNydpWwQdOlT5sxtjTMCVpoXeF9gsIkkichyYDYwosM7twIsish9ARPb6t8xSSEuD6Gj27LFJuYwx4ak0gd4K2JHndop3WV5nAmc65750zq10zg0tbEPOuTuccwnOuYS0tLTyVVyUtDQkOpq0NDit6j8fGGNMwPnroGhNoDMwGBgD/N0517jgSiIyQ0TiRSQ+OjraT0/tlZbG8YbReDwQE+PfTRtjTDAoTaDvBNrkud3auyyvFGC+iJwQkWTgRzTgq05aGj/X1TcJa6EbY8JRaQJ9FdDZOdfBOVcLGA3ML7DOh2jrHOdcc7QLJsmPdRYvOxsyMjhQSwPdWujGmHBUYqCLSDYwEVgEbALmiMhG59wTzrnh3tUWARnOuURgCfCAiGRUVtGnyNCnyqipTXNroRtjwlGJwxYBRGQBsKDAskfzXBfgPu+l6nkPsO71WAvdGBO+QuNMUW+g7zoRTc2a0KRJgOsxxpgACKlA334kmuhoqBEav5UxxpRJaESfN9CTs6Ktu8UYE7ZCKtC3ZDazA6LGmLAVGoG+dy80a8auvTWthW6MCVuhEeje0/737rUhi8aY8BUygZ7TNJojR2zIojEmfIVMoB9tYGPQjTHhLWQCPSvK5nExxoS34A/0nBzIyCAz0gLdGBPegj/Q9+0Dj4c075ck2ZdbGGPCVfAHuncM+u7saGrUsBa6MSZ8hUygbz8SzemnQ0REgOsxxpgACZlATzoUbd0txpiwFjKB/uP+aFq2DHAtxhgTQCET6Il7m1ugG2PCWvAH+t69SJMm7E6PtC4XY0xYC/5AT0sju4mOQbcWujEmnIVEoB+tb4FujDEhEeiHoizQjTEmJAJ9f00NdOtDN8aEs+AOdI8H0tNJc6cREQHR0YEuyBhjAie4A33/fsjJYdcJO0vUGGOCO9DznPZv3S3GmHBXqkB3zg11zv3gnNvsnJtcyP3jnHNpzrl13stt/i+1EHlO+7cDosaYcFezpBWccxHAi8AlQAqwyjk3X0QSC6z6LxGZWAk1Fi1PoHewWRaNMWGuNC30vsBmEUkSkePAbGBE5ZZVSnv3ApCcFU2TJgGuxRhjAqw0gd4K2JHndo6bw+kAABJVSURBVIp3WUHXOue+dc7Ndc61KWxDzrk7nHMJzrmENG/rukJ270Zq1GDbsRgaN6745owxJpj566Dox0B7EekBfAbMLGwlEZkhIvEiEh/tjzGGO3fiiY4hh5oW6MaYsFeaQN8J5G1xt/YuO0lEMkTkmPfma0Af/5RXgl27ON5cj4Zal4sxJtyVJtBXAZ2dcx2cc7WA0cD8vCs45/IOGhwObPJficXYtYsjTTTQrYVujAl3JY5yEZFs59xEYBEQAbwhIhudc08ACSIyH7jbOTccyAb2AeMqseZcu3aRFd8PsEA3xpgSAx1ARBYACwosezTP9YeAh/xbWgmOHYO0NDLrWZeLMcZAMJ8pumcPABm1dcCNtdCNMeEueAN91y4AUiOsD90YYyAEAn23a0lUFERFBbgeY4wJsOAN9J06cnJHTktrnRtjDMEc6Lt2QWQkKUeaWaAbYwzBHugtW7L/QA0b4WKMMYRAoGdm2gFRY4yBYA70nTu1hb7fAt0YYyCYA333bmjRgsxMO6nIGGMgWAP9xAk4cABpHm1dLsYY4xWcgZ6eDsCxhtHk5FigG2MMBHmgZ0U1B6zLxRhjIMgD/WAtDXRroRtjTJAH+r4I/dYjC3RjjAnyQM9w1kI3xhif4Ax07xdM781pBlgfujHGQLAGeno6NGrEvkORgLXQjTEGgjnQo3UMOkCjRoEtxxhjqoPgDfTmzcnMhAYNoGapvkjPGGNCW3AGeloaNG9u87gYY0wewRnoebpcLNCNMUYFX2eFSG6XS5KNcDHB7cSJE6SkpHD06NFAl2KqmaioKFq3bk1kZGSpHxN8gX74MBw9erLLpX37QBdkTPmlpKTQoEED2rdvj3Mu0OWYakJEyMjIICUlhQ4dOpT6caXqcnHODXXO/eCc2+ycm1zMetc658Q5F1/qCsrKe1KR76CodbmYYHb06FGaNWtmYW7ycc7RrFmzMn9yKzHQnXMRwIvA5UBXYIxzrmsh6zUAJgFfl6mCsvKeVOTrQ7cuFxPsLMxNYcrzuihNC70vsFlEkkTkODAbGFHIek8CTwOV2xnobaHnNGnOwYPWQjfGGJ/SBHorYEee2yneZSc553oDbUTk38VtyDl3h3MuwTmXkOZraZeVN9AP1bZ5XIwxJq8KD1t0ztUAngXuL2ldEZkhIvEiEh8dHV2+J/QGemakPt66XIypmMzMTF566aUyP27YsGFk+k7XNtVCaUa57ATa5Lnd2rvMpwHQDVjq7fM5HZjvnBsuIgn+KvSkPn3gwQfJyNbz/a2FbkLFPffAunX+3WbPnjBtWvHr+AL9zjvvzLc8OzubmsWchr1gwQJ/lFhpSqo/FJWmhb4K6Oyc6+CcqwWMBub77hSRAyLSXETai0h7YCVQOWEOMGAAPP00mQf0gIEFujEVM3nyZLZs2ULPnj0555xzGDBgAMOHD6drVx37cPXVV9OnTx9iY2OZMWPGyce1b9+e9PR0tm7dSpcuXbj99tuJjY3l0ksv5ciRI0U+39///nfOOecc4uLiuPbaazl8+DAAqampXHPNNcTFxREXF8dXX30FwFtvvUWPHj2Ii4vjpptuAmDcuHHMnTv35Dbr168PwNKlS0td/8KFC+nduzdxcXEMGTIEj8dD586d8XUHezwezjjjDMrdPRwIIlLiBRgG/AhsAaZ4lz2BBnfBdZcC8SVts0+fPlIRc+eKgMj69RXajDEBlZiYGOgSJDk5WWJjY0VEZMmSJVK3bl1JSko6eX9GRoaIiBw+fFhiY2MlPT1dRETatWsnaWlpkpycLBEREbJ27VoRERk1apS8/fbbRT6f7/EiIlOmTJHp06eLiMj1118vzz33nIiIZGdnS2ZmpmzYsEE6d+4saWlp+Wq5+eab5b333ju5nXr16pWp/r1790rr1q1PrudbZ+rUqSdrWLRokYwcObK0u7FSFPb6ABKkiFwt1ecREVkALCiw7NEi1h1crneWMtq/X39aC90Y/+rbt2++k1mmT5/OvHnzANixYwc//fQTzZo1y/eYDh060LNnTwD69OnD1q1bi9z+hg0beOSRR8jMzCQrK4vLLrsMgMWLF/PWW28BEBERQaNGjXjrrbcYNWoUzZvrIIimTZv6pf60tDQGDhx4cj3fdm+55RZGjBjBPffcwxtvvMH48eNLfL7qJGg7mHzHYizQjfGvevXqnby+dOlS/vvf/7JixQrq1q3L4MGDCz3ZpXbt2ievR0REFNvlMm7cOD788EPi4uJ48803Wbp0aZlrrFmzJh6PB9CukePHj1eofp82bdoQExPD4sWL+eabb5g1a1aZawuk4JycCw30GjV0+lxjTPk1aNCAQ4cOFXrfgQMHaNKkCXXr1uX7779n5cqVFX6+Q4cO0aJFC06cOJEvMIcMGcLLL78MQE5ODgcOHOCiiy7ivffeIyMjA4B9+/YB2n+/evVqAObPn8+JEyfKVH+/fv34/PPPSU5OzrddgNtuu42xY8cyatQoIiIiKvz7VqWgDXTf1Ll2kp0xFdOsWTP69+9Pt27deOCBB/LdN3ToULKzs+nSpQuTJ0+mX79+FX6+J598knPPPZf+/ftz9tlnn1z+/PPPs2TJErp3706fPn1ITEwkNjaWKVOmMGjQIOLi4rjvvvsAuP3221m2bBlxcXGsWLEiX6u8NPVHR0czY8YMRo4cSVxcHDfccMPJxwwfPpysrKyg624BcNrHXvXi4+MlIaH8A2FuvBFWroQtW/xYlDFVbNOmTXTp0iXQZZg8EhISuPfee1m+fHmgSyn09eGcWy0ihc6XFdR96HZSkTHGn5566ilefvnloOs79wn6LhdjTPV011130bNnz3yXf/zjH4Euq1iTJ09m27ZtXHDBBYEupVyCuoXesmWgqzDGFOXFF18MdAlhJ2hb6NblYowx+QVloB8/DqmpEBMT6EqMMab6CMpA37YNPB7o3DnQlRhjTPURlIG+ebP+POOMwNZhjDHViQW6MaZMfDMb7tq1i+uuu67QdQYPHkxJ55lMmzbt5EyLYPOr+0NQjnLZvBnq14fTTgt0Jcb4UaAmRC+nli1b5pvCtqymTZvG2LFjqVu3LlD951cvSnWadz1oW+hnnGGn/RvjD5MnT843xHDq1Kn84Q9/YMiQIfTu3Zvu3bvz0UcfnfK4rVu30q1bNwCOHDnC6NGj6dKlC9dcc02+ybkmTJhAfHw8sbGxPPbYY4DOgLhr1y4uvPBCLrzwQiB3fnWAZ599lm7dutGtWzemed+QbN71UihqXt3KvlRkPvQzzxS57rpyP9yYaqM6zIe+Zs0aGThw4MnbXbp0ke3bt8uBAwdERCQtLU06deokHo9HRHLnHs87j/pf//pXGT9+vIiIrF+/XiIiImTVqlUikjvXeHZ2tgwaNEjWe7/EwDefuo/vdkJCgnTr1k2ysrLk0KFD0rVrV1mzZk1Yzrte1vnQg66Fnp0NycnWf26Mv/Tq1Yu9e/eya9cu1q9fT5MmTTj99NN5+OGH6dGjBxdffDE7d+4kNTW1yG18/vnnjB07FoAePXrQo0ePk/fNmTOH3r1706tXLzZu3EhiYmKx9XzxxRdcc8011KtXj/r16zNy5MiT86qUdd71AQMG0L17d2bNmsXGjRsBnXd9woQJQO6864sXL/bLvOtxcXH069fv5LzrK1euLHLedd/c7/6cd716dPyUwY4dcOKEBbox/jRq1Cjmzp3Lnj17uOGGG5g1axZpaWmsXr2ayMhI2rdvX+w84kVJTk7mmWeeYdWqVTRp0oRx48aVazs+Nu968YKuhW4jXIzxvxtuuIHZs2czd+5cRo0axYEDBzjttNOIjIxkyZIlbNu2rdjHDxw4kHfeeQfQlvG3334LwMGDB6lXrx6NGjUiNTWVTz/99ORjipqHfcCAAXz44YccPnyYn3/+mXnz5jFgwIAy/07hOO+6BboxhtjYWA4dOkSrVq1o0aIFN954IwkJCXTv3p233nor37zlhZkwYQJZWVl06dKFRx99lD59+gAQFxdHr169OPvss/nFL35B//79Tz7mjjvuYOjQoScPivr07t2bcePG0bdvX84991xuu+02evXqVebfKRznXQ+6+dA/+gjefBPef1+/sciYYGbzoYev0sy7HvLzoY8YoRdjjAlWlTXvurVxjTFBzeZdzxV0LXRjQo2I4OwsuXIL1XnXy9Mdbi10YwIoKiqKjIyMcv3zmtAlImRkZBAVFVWmx5Wqhe6cGwo8D0QAr4nIUwXu/zVwF5ADZAF3iEjxZw8YY2jdujUpKSn+Oe3bhJSoqChat25dpseUGOjOuQjgReASIAVY5ZybXyCw3xGRV7zrDweeBYaWqRJjwlBkZGS+sw2NqYjSdLn0BTaLSJKIHAdmA/nGmYjIwTw36wH2+dEYY6pYabpcWgE78txOAc4tuJJz7i7gPqAWcFFhG3LO3QHcAdC2bduy1mqMMaYYfjsoKiIvikgn4HfAI0WsM0NE4kUkPjo62l9PbYwxhtK10HcCbfLcbu1dVpTZwMslbXT16tXpzrniJ4goWnMgvZyPrWzVtTarq2ysrrKrrrWFWl3tirqjNIG+CujsnOuABvlo4Bd5V3DOdRaRn7w3rwB+ogQiUu4munMuoahTXwOtutZmdZWN1VV21bW2cKqrxEAXkWzn3ERgETps8Q0R2eicewKdaH0+MNE5dzFwAtgP3OzPIo0xxpSsVOPQRWQBsKDAskfzXJ/k57qMMcaUUbCeKTqj5FUCprrWZnWVjdVVdtW1trCpK2DT5xpjjPGvYG2hG2OMKcAC3RhjQkTQBbpzbqhz7gfn3Gbn3OQA1tHGObfEOZfonNvonJvkXT7VObfTObfOexkWgNq2Oue+8z5/gndZU+fcZ865n7w/m1RxTWfl2SfrnHMHnXP3BGp/OefecM7tdc5tyLOs0H3k1HTva+5b51zvKq7rL865773PPc8519i7vL1z7kieffdKFddV5N/OOfeQd3/94Jy7rLLqKqa2f+Wpa6tzbp13eZXss2LyoXJfYyISNBd02OQWoCM6xcB6oGuAamkB9PZebwD8CHQFpgK/DfB+2go0L7Dsz8Bk7/XJwNMB/jvuQU+QCMj+AgYCvYENJe0jYBjwKeCAfsDXVVzXpUBN7/Wn89TVPu96Adhfhf7tvP8H64HaQAfv/2xEVdZW4P6/Ao9W5T4rJh8q9TUWbC30EicKqyoisltE1nivHwI2ofPeVFcjgJne6zOBqwNYyxBgi4iU90zhChORz4F9BRYXtY9GAG+JWgk0ds61qKq6ROQ/IpLtvbkSPVu7ShWxv4oyApgtIsdEJBnYjP7vVnltzjkHXA+8W1nPX0RNReVDpb7Ggi3QC5soLOAh6pxrD/QCvvYumuj92PRGVXdteAnwH+fcaqcTogHEiMhu7/U9QEwA6vIZTf5/sEDvL5+i9lF1et3dgrbkfDo459Y655Y55wYEoJ7C/nbVaX8NAFIl90x2qOJ9ViAfKvU1FmyBXu045+oD7wP3iE4j/DLQCegJ7EY/7lW1C0SkN3A5cJdzbmDeO0U/4wVkvKpzrhYwHHjPu6g67K9TBHIfFcU5NwXIBnzfLLwbaCsivdCZTt9xzjWswpKq5d+ugDHkbzxU6T4rJB9OqozXWLAFelknCqtUzrlI9I81S0Q+ABCRVBHJEREP8Hcq8aNmUURkp/fnXmCet4ZU30c478+9VV2X1+XAGhFJ9dYY8P2VR1H7KOCvO+fcOOBK4EZvEODt0sjwXl+N9lWfWVU1FfO3C/j+AnDO1QRGAv/yLavKfVZYPlDJr7FgC/STE4V5W3qjgfmBKMTbN/c6sElEns2zPG+/1zXAhoKPreS66jnnGviuowfUNqD7yTfHzs3AR1VZVx75WkyB3l8FFLWP5gO/9I5E6AccyPOxudI5/QrIB4HhInI4z/Jop98ohnOuI9AZSKrCuor6280HRjvnajud1K8z8E1V1ZXHxcD3IpLiW1BV+6yofKCyX2OVfbTX3xf0aPCP6DvrlADWcQH6celbYJ33Mgx4G/jOu3w+0KKK6+qIjjBYD2z07SOgGfA/dCbM/wJNA7DP6gEZQKM8ywKyv9A3ld3ohHIpwK1F7SN05MGL3tfcd0B8Fde1Ge1f9b3OXvGue633b7wOWANcVcV1Ffm3A6Z499cPwOVV/bf0Ln8T+HWBdatknxWTD5X6GrNT/40xJkQEW5eLMcaYIligG2NMiLBAN8aYEGGBbowxIcIC3RhjQoQFujHGhAgLdGOMCRH/DxRzKJ0hFbdkAAAAAElFTkSuQmCC\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWoAAAD4CAYAAADFAawfAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3deXxU5b3H8c+ThSwsIYQACQEJgmwugAHxItbWthcRxSporRtqS7W0StX24qub66ut9XqtV4WrFeu1KlIt6rVSWxXFFWWNrAIaBBIJJECALGR57h+/GRIwgQSTmZPk+3695pXJLOf85szM9zznOc8547z3iIhIcMVEuwARETkyBbWISMApqEVEAk5BLSIScApqEZGAi2uJiXbv3t3369evJSYtItImLV26dKf3Pr2++1okqPv168eSJUtaYtIiIm2Sc25zQ/ep60NEJOAU1CIiAaegFhEJuBbpoxaRyKmsrGTr1q2Ul5dHuxRphMTERLKysoiPj2/0cxTUIq3c1q1b6dy5M/369cM5F+1y5Ai89xQVFbF161ays7Mb/Tx1fYi0cuXl5aSlpSmkWwHnHGlpaU3e+lFQi7QBCunW41jeq0AF9Z13wquvRrsKEZFgCVRQ33OPglpE5HCBCurkZCgri3YVItIUu3fv5uGHH27y8yZMmMDu3bub/LypU6fy3HPPNfl5rVmggjopCUpLo12FiDRFQ0FdVVV1xOe98sordO3ataXKalMCNTwvOVlBLfJVzJgBK1Y07zSHD4f772/4/pkzZ7Jp0yaGDx9OfHw8iYmJpKamsm7dOj755BMuuOACtmzZQnl5OTfeeCPTpk0Das8JtG/fPs455xzOOOMM3nvvPXr37s2LL75IUlLSUWt7/fXXueWWW6iqqmLUqFHMmjWLhIQEZs6cyUsvvURcXBzf/va3uffee/nrX//K7bffTmxsLCkpKSxatKi5FlGLU1CLyFfyu9/9jlWrVrFixQrefPNNzj33XFatWnVwnPCcOXPo1q0bZWVljBo1iosuuoi0tLRDprFhwwaeeeYZHn30US6++GKef/55Lr/88iPOt7y8nKlTp/L6669zwgkncOWVVzJr1iyuuOIK5s+fz7p163DOHexeueOOO3j11Vfp3bv3MXW5RFPgglp91CLH7kgt30gZPXr0IQdzPPDAA8yfPx+ALVu2sGHDhi8FdXZ2NsOHDwfg1FNPJS8v76jzWb9+PdnZ2ZxwwgkAXHXVVTz00EP8+Mc/JjExkWuvvZaJEycyceJEAMaOHcvUqVO5+OKLufDCC5vjpUaM+qhFpFl17Njx4PU333yT1157jffff5+VK1cyYsSIeg/2SEhIOHg9Njb2qP3bRxIXF8eHH37I5MmTefnllxk/fjwAs2fP5q677mLLli2ceuqpFBUVHfM8Ii1wLeqCgmhXISJN0blzZ/bu3VvvfXv27CE1NZXk5GTWrVvHBx980GzzHTRoEHl5eWzcuJEBAwbw5JNP8rWvfY19+/ZRWlrKhAkTGDt2LP379wdg06ZNnHbaaZx22mksWLCALVu2fKllH1SBC2q1qEVal7S0NMaOHcuJJ55IUlISPXv2PHjf+PHjmT17NkOGDGHQoEGMGTOm2eabmJjI448/zpQpUw7uTLzuuusoLi5m0qRJlJeX473nvvvuA+BnP/sZGzZswHvP2WefzSmnnNJstbQ0571v9onm5OT4Y/mFlx/8AF55BbZta/aSRNqstWvXMmTIkGiXIU1Q33vmnFvqvc+p7/HqoxYRCTh1fYhIIE2fPp133333kNtuvPFGrr766ihVFD2BC+oDB6C6GmJjo12NiETTQw89FO0SAiNQXR/JyfZXY6lFRGoFKqjDR4yq+0NEpFajg9o5F+ucW+6ce7mligm3qBXUIiK1mtKivhFY21KFgLo+RETq06igds5lAecCf2rJYtSiFmn7OnXqBEB+fj6TJ0+u9zFnnXUWRzsW4/7776e0Tlgc6/mtGxKk8143tkV9P/BzoKYFa1EftUg7kpmZ+ZWC8PCgbsvntz7q8Dzn3ESg0Hu/1Dl31hEeNw2YBtC3b99jKkYtapGvKAonpJ45cyZ9+vRh+vTpANx2223ExcWxcOFCdu3aRWVlJXfddReTJk065Hl5eXlMnDiRVatWUVZWxtVXX83KlSsZPHgwZXX6P6+//no++ugjysrKmDx5MrfffjsPPPAA+fn5fP3rX6d79+4sXLjw4Pmtu3fvzn333cecOXMA+P73v8+MGTPIy8trtee9bkyLeixwvnMuD5gLfMM595fDH+S9f8R7n+O9z0lPTz+mYtRHLdL6XHLJJcybN+/g//PmzeOqq65i/vz5LFu2jIULF3LzzTdzpNNVzJo1i+TkZNauXcvtt9/O0qVLD9539913s2TJEnJzc3nrrbfIzc3lhhtuIDMzk4ULF7Jw4cJDprV06VIef/xxFi9ezAcffMCjjz7K8uXLATvv9fTp01m9ejVdu3bl+eefP+rrC5/3+tlnn+Xjjz+mqqqKWbNmUVRUxPz581m9ejW5ubn88pe/BGrPe71y5UpeeumlJi3Lhhy1Re29vxW4FSDUor7Fe3/kM3ofI7WoRb6iKJyQesSIERQWFpKfn8+OHTtITU2lV69e/PSnP2XRokXExMSwbds2tm/fTq9eveqdxqJFi7jhhhsAOPnkkzn55JMP3jdv3jweeeQRqqqqKCgoYM2aNYfcf7h33nmH73znOwdPt3rhhRfy9ttvc/7557fa815rHLWIfGVTpkzhueee49lnn+WSSy7hqaeeYseOHSxdupQVK1bQs2fPes9DfTSfffYZ9957L6+//jq5ubmce+65xzSdsNZ63usmBbX3/k3v/cSvPNcGqOtDpHW65JJLmDt3Ls899xxTpkxhz5499OjRg/j4eBYuXMjmzZuP+PwzzzyTp59+GoBVq1aRm5sLQElJCR07diQlJYXt27ezYMGCg89p6DzY48aN44UXXqC0tJT9+/czf/58xo0bd8yvre55r4FDznu9Z88eJkyYwH/913+xcuVKoPa813fccQfp6els2bLlmOcdFrhzfYBa1CKtzbBhw9i7dy+9e/cmIyODyy67jPPOO4+TTjqJnJwcBg8efMTnX3/99Vx99dUMGTKEIUOGcOqppwJwyimnMGLECAYPHkyfPn0YO3bswedMmzaN8ePHH+yrDhs5ciRTp05l9OjRgO1MHDFiRKO6OeoThPNeB+p81N5DTAz8+tdw++3NXpZIm6TzUbc+rfp81M7pnNQiIocLVNcH6JfIRSSyWsN5rwMZ1GpRizSN9x7nXLTLaJUifd7rY+luDlTXByioRZoqMTGRoqKiYwoAiSzvPUVFRSQmJjbpeYFrUauPWqRpsrKy2Lp1Kzt27Ih2KdIIiYmJZGVlNek5gQtq9VGLNE18fDzZ2dnRLkNakLo+REQCTkEtIhJwgQvqpCR1fYiI1BW4oFaLWkTkUApqEZGAU1CLiARc4II63EetsfsiIiZwQR0+1elXODe4iEibEtig3r8/unWIiARF4IK6Uyf7q6AWETHBCur0dMb83y8A2LcvyrWIiAREsIK6upqkGkvoen4KTUSkXQpWUCcnk1htY/PUohYRMYEL6g4KahGRQwQvqKsU1CIidQUuqOMPKKhFROoKXFDHKahFRA4RuKCOqVBQi4jUFbigdvv307GjhueJiIQFLqgpLaVTJ7WoRUTCFNQiIgEXyKDu3FlBLSISFrygLiujc8caBbWISEjwghrollyuoBYRCQlmUCeWKqhFREICGdSpCaUaniciEhLYoFaLWkTEBDKoU+IV1CIiYYEM6i5xpVRWwoEDUa5HRCQAAhvUoLHUIiIQ0KDuHKugFhEJO2pQO+cSnXMfOudWOudWO+dub7FqQkHdKUZBLSISFteIx1QA3/De73POxQPvOOcWeO8/aPZqQkGd7CyoNURPRKQRQe2990C4bRsfuvgWqSYc1F4tahGRsEb1UTvnYp1zK4BC4F/e+8X1PGaac26Jc27Jjh07jq2aUFAnKahFRA5qVFB776u998OBLGC0c+7Eeh7ziPc+x3ufk56efmzVJCSAcyTWKKhFRMKaNOrDe78bWAiMb5FqnIPkZBKqFdQiImGNGfWR7pzrGrqeBHwLWNdiFSUn06FKQS0iEtaYUR8ZwBPOuVgs2Od5719usYqSk4mrVFCLiIQ1ZtRHLjAiArWY5GRiykpJTtbwPBERCNqRiXDI7yYqqEVEAhzUnTsrqEVEIMBBnZICJSXRLkZEJPoCG9RduiioRUQg4EG9Z0+0ixERib5AB7Va1CIiAQ5q9VGLiJjABnW4Re1b5jx9IiKtRjCDurKSrh0rqaqCsrJoFyQiEl3BDGogLckOI1f3h4i0d8EL6i5dAOgWZwmtoBaR9i54Qd2tm/2hGFBQi4gEL6hTUwHo6ncBGkstIhK8oA61qLtUqUUtIgJBDOpQi7pTpbWoFdQi0t4FNqiTK9T1ISICQQzqTp0gLo7EUnV9iIhAEIPaOUhNJbZkF4mJCmoRkeAFNdgOxeJinZhJRISgBnVqKuzaRUqK+qhFRIIZ1GpRi4gcFMygDrWoFdQiIkEN6m7dDnZ9KKhFpL0LZlCnpsLu3aR0rlEftYi0e8ENau/pkbBHLWoRafeCGdSh8330jC/Wr7yISLsXzKAOHUaeHreL6mooLY1yPSIiURTMoA6fk9rpxEwiIsEM6lCLOvzjAcXF0SxGRCS6ghnUoRZ191hrUW/fHs1iRESiK5hBHf6VlxprSiuoRaQ9C2ZQJyRAUhKdq9WiFhEJZlADpKWRuG8n8fEKahFp34Ib1BkZuIICevRQUItI+xbcoM7MhIICevZUUItI+xbcoM7IgPx8BbWItHvBDerMTNi5k8zuBxTUItKuBTeoMzIAOL7TFxQW6nwfItJ+HTWonXN9nHMLnXNrnHOrnXM3RqIwMjMB6Befz4EDsHt3ROYqIhI4jWlRVwE3e++HAmOA6c65oS1bFgeDOtMVAOqnFpH266hB7b0v8N4vC13fC6wFerd0YeGuj57V+YCCWkTaryb1UTvn+gEjgMX13DfNObfEObdkx44dX72y9HSIjaVbuYJaRNq3Rge1c64T8Dwww3v/pROPeu8f8d7neO9z0tPTm6GyGOjVi8771PUhIu1bo4LaORePhfRT3vu/tWxJdWRmklicT0wMFBZGbK4iIoHSmFEfDngMWOu9v6/lS6ojIwP3RQHp6WpRi0j71ZgW9VjgCuAbzrkVocuEFq7LZGZCfj69ekFBQUTmKCISOHFHe4D3/h3ARaCWL8vIgJ07OS7nAFvzO0SlBBGRaAvukYlwcCz14K5fsG1blGsREYmSVhHUAzvmU1gIlZVRrkdEJAqCHdShg16O61CA9/DFF1GuR0QkCoId1KEWdYa3g17U/SEi7VGwgzp0dGL3KhvykZ8f5XpERKIg2EEdOjoxZZ9a1CLSfgU7qAEyMkgszic+Xi1qEWmfgh/UmZm4LwrIzFSLWkTap1YR1OTnK6hFpN0KflCHj07MOKCuDxFpl4If1KEheoNSdHSiiLRPwQ/q8I/cJuWzdy/s3RvlekREIiz4QR1qUfeNt7HUalWLSHsT/KAOH0Yebx3Ua9dGsxgRkcgLflCHjk7sHVNATAysWBHtgkREIiv4QR0bCz17El+4jcGDYfnyaBckIhJZwQ9qgOxs2LSJ4cPVohaR9qd1BPWwYbB6NSOGe7ZsgaKiaBckIhI5rSOohw6F4mJG97OfIlerWkTak9YR1MOGAXBK3GpAQS0i7UvrCOqhQwFI2bqarCztUBSR9qV1BHVGBnTtCmvWMHQofPJJtAsSEYmc1hHUzh3codivH3z2WbQLEhGJnNYR1GDdH6tXk93Ps3Mn7NsX7YJERCKj9QT1sGFQXMzgrvZT5Hl50S1HRCRSWk9Qn3kmAKe9fS+g7g8RaT9aT1CPGAE//CG9nr2fHD5Si1pE2o3WE9QAv/899OjBHTG3q0UtIu1G6wrqlBTc2WczPCZXQS0i7UbrCmqAIUPIqNrC9k0a9iEi7UOrDGqADp+ui3IhIiKR0WqDus/+tezeHeVaREQioPUF9YAB1MTGMYS1zJsHNTXRLkhEpGW1vqCOj8f3H8Dozmv54Q9h2rRoFyQi0rJaX1ADsScO4ezMtUyeDC+8AN5HuyIRkZbTKoOaIUNwGzfyjTMOUFQE27ZFuyARkZbTaoOa6mrGdN8I6IcERKRta51BfdJJAAwuX4FzCmoRaduOGtTOuTnOuULn3KpIFNQow4ZBUhJJqz5iwAAFtYi0bY1pUf8ZGN/CdTRNXByMHAkffsjw4QpqEWnbjhrU3vtFQHEEammaUaNg+XJGnFTFpk1QUhLtgkREWkaz9VE756Y555Y455bs2LGjuSbbsFGjoKyMM1Ltl8mXLWv5WYqIREOzBbX3/hHvfY73Pic9Pb25JtuwUaMAOLXmQzp2hD/9qeVnKSISDa1z1AfAgAHQtSvJqz5i2jSYOxc2b452USIiza/1BrVzMHYsvPgiN00txjm4775oFyUi0vwaMzzvGeB9YJBzbqtz7tqWL6uR7roLiovJuu8mLr8cZs+G9eujXZSISPNqzKiPS733Gd77eO99lvf+sUgU1ijDh8N//Ac88QT/3eNOOiVVc911OveHiLQtrbfrI+xXv4JLL6XTPb9mRdZE3n6ziptugurqaBcmItI8Wn9QJyTAU0/Bgw/SZ/U/eHXETO6/Hy65RC1rEWkbWn9Qg+1YnD4dpk/n7OX/ydNXLOD552HBgmgXJiLy1TnfAs3OnJwcv2TJkmaf7lEdOADDhlGT3JFB+5aR1DGG5cshNjbypYiINIVzbqn3Pqe++9pGizqsQwf4zW+IyV3J/058li8+LmTWw+r/EJHWrW0FNcCll8KQIZz+wPcopCf9b5zI+y8WRrsqEZFjFhftAppdbKztXHzpJcr3VXL2f97L9gtPo+jztaT1Tox2dSIiTdb2ghpgxAgYMYJE4LPssWRPn8DjFz/J1e/+INqViYg0Wdvr+jhM9vXj2dZrJGPf+wOv/ehv+Jm3wv790S5LRKTR2nxQ4xzpf/gPTmAD35x1Ee73v6P01HGwZcuhj6usjE59IiJH0faDGuhw6UX4H0zjg0v/yJUpL1K1fiMlg0dT9cLLMGcOnHEGpKTAO+9Eu1QRkS9pW+OoG6GkBB744Wq+N/c8+vOZ3di/vx1zXlYGH30EfftGt0gRaXfazzjqRujSBX75zDCWPPwRl7h53PCNVcy+eQM/7LuAA3vLqblqau2x5wUFcOWVsH17VGsWkfatbY76aISLr0+j4MAUZswA3oDu3YcQX3Y3D775E7bM/jt9rp8IP/uZDfXr2RP+8Idolywi7VS7a1HXdcMN8OCDMG+eNZrPfvaHbIw9gdLpt/DWNU9YSHfpQs3s/6Fww57aJx44YL9SsHFj9IoXkXajXQd1+FxOU6ZATAx85+J4Uv98PwPYyNcen8rOxN787ZqXidm3l1eHzuCtyx/F79gJN99sl5Ej4dZb4cYbYd066zJ58kn4/PNovzQRaUPa3c7ExqjO387LM9/hnhdP4L2Sk3inyzmMLfkHAJUdOhJ/YD9cey2sXQvvvQdxcZCRARdeCH/8ox1w88Yb9qMGY8daP7eIyBEcaWeigvoI9u61QSBnnFZJ/K5Crr+okHOX3UnOKLiyw7Msy42jU2wZ08at5dYF44gpL7NgfvddSE+HHTtsQtddB0OHQl4e7NljP3Zw3HF2X3W1XTp0sP+9t98TGzTImvwi0i4oqJvJhg1w0klQUQGZmXD++bB7N7z0EpxV8SozTnqdHTPuZvzffkDq3/9Cwe/+l/T1bxP/p9k2gcREC9+kJOtzOXAAHn/cAj0rC845x7pQFi2yML/jDgv2jh3teZ99BmlpkJoa3QUhIs1OQd2M5syBZcvgzjtr83L7duvleOYZy94YqunFF+TTm5QU+NFle/jNzAoSMrpZq/qyy+DDDy18zz3X+rrXrLFfOkhOtrXBG2/Yfa+8AvHxdgkf+n7ccTaN00+3bpfly20oYXIy3HILdO8O5eXw5z9Ddjb8+79Ha3GJSCMpqCOkshI++QRycy0309Lgn/+Ep5+G8eNttN/mzXDyyXDK0Eriqsqhc+eDz/flFVT7GOJcNXztazahadOsJV5WBqecYk3411+HV1+FmpramXftCvv22dpj3DhbEWzdavfNmGFHXm7cCMXFFuann27TWLLECh8zBr75TWvB//d/w4ABMHnyl1vvFRWwcCH8/e+28jj9dPjOd2yF0VzKymq3PkTaCQV1lD32GPzgB4f+huMJJ8A991hohzP0yist4C+5BH55cxl9e5Q33M1RVASbNtUGeNeusGqVjTn84gtrSf/kJzb28PHHLfT69oWqKti2zY78KSmx08LGxtqmQFKSPa6szIrt0AEmToRvfcu6X15+2Vr9e/da672mxlrup5xixScm2m9Y5ufbPH7yExg8GBYvtnqLimxEzOef2wojLs6mf+mlFvolJfDAA/Db38IFF8Bf/vLlsK6uhl27bKuhKTZvtrXoWWfZvBpSXm6vQyTCFNQBsHix5Ut2tjV277zT+rzrysqyHHn+eRsuOGmSNYq9t2NuzjoLunWz/ZRf/3oTfmKsoMCemJAApaU284ICuPxy2/kZE2MFzp1rQfWrX1mQPvmk3RY+MrNnT+uYnzQJzj7bgvaFF+Cmmw49yZVzNi/vbTRMXt6h9WRk2ObGnj32vK5d4fjjbUVTUWFdQcuWwY9/DD162Ciaf/s3Wwm9+KJtOZx/vnX/dOgAn34KH3wAH39sa8TUVPjNb2D0aKt12TKYNcum3bs3XH89XHWVvZ5337W15JQptlz++Ecb0TN0qIX7jBn2nDVrrMupuNi2JsJvTGamrfz69bOVS90Vy7/+BW+/DTk59qa+954994QT7H0I/6jnmWfam1paal1dAwfa+/D227ZllZNj842JsZVpQkL9Wxs1NTaN7dvtQ7Z4sV1/8EH7sMyZUzu/nBxbMb73ni2/Cy6w13K4XbtsOZx00pc/cKWl8MQTNt8zz4Rhw2wl/NFHcN55tkL84ANbWael1f/ZrKmxxsSYMbYMj6amBgoLrbFQU2OXvXutzk6d7PV++qk1HHr0OPr0wD4X8fG2fOu+tpIS+4ynpBx55V5Xaak1Yo6BgjqAKirse7xzp+VVdTVMnWp5mpdnGbVsmfVAxMdbltQdnt2/v+2PvPxy+1wUFcHSpfC3v1kO3HSTTTc1tfZzU1RkOXHhhfaZbhTv7Yu6a5e1nGPqGXpfXW1flooKu6SmWqt8xgz7Ul17rYVP167Qp48FTXjaCxZY+G7aBCeeCN/7HowaZV+0v/yldh4dO1qr/5prbCE9/LC9wLCsLAvUxYvt/5EjbaGVlFiofe97Fh6PPWYL/nCJiRaO48bB++9b+MbE2Jc0I8OC2rnazaLYWPu/qqp2GlOmWO2ffgorVlhIhSUk2Dx69LCtiD/9yZYZ1O6rWL3adhgfLj7+y2d3TEy05Zydbdd37bLhouXltY9JSrLnnXmm3f7ee7XzO+88ePNNWz7h5Xv55bYyGjXKVoBPPWUr67IyW+YjR9o8V6+2ZbNjx6GnV0hJsel5byvJxETbMe6cfXYGDbLnJiTAz38Op55qjYJnnrHHzpxpW2GpqdZneMcdtkJMTbUvRG4uPProoa+xISedZMc4PPSQdRcmJtqKqHdvu2Rm2udp8WKbf7dutpy2bbMtr8I6vwoVE2Of31GjrGGzZ4+99qoqWyZjxth79Mtf2udkyZJj+qFWBXUb4L01PsvKYOVK60au72R/qan2nY2NtfxMS7OcLCmxvvKSEmu8/va3MHy4fc/r614OZ26XLi3/2upVU2PDFDMzrdX24ovw+99bSxAs5PLy7MvWr5+9UO/hr3+1L9n119vO1y1b7EXWbeWsW2dBsHOnrRx694Z777Uv3M9/blsbVVW2AL7/fWvBf//7Nt3ERLjoIltTgk0jPh7+53/sixpe6P37W5fO1Km2s3fQIKv3G9+wx3z3u7bSSU6G//s/C+5u3aw/bPduC4czzoB//MNWYr172+srK6u9FBXZSqGqyvZ1DB1qK5XUVAvBYcNsZXfNNTa9uXNts+zuu63eiRNt6Gh6Otx1l+2zCAc3WNBfeqkF2KJFFpTFxbbMwivsn/7UutQWLbIPZEZGbbcb2LyKi23lt369ta7z8ux62K9/bQH33HM2z9hYW+b9+lm9K1faMoyJgSuusJVASor975ytZLp1s+d06WJBesEF9v4NHGj9i/v313bJFRXVzrtjR3uNRUUWsNnZ1tLJzraGRXW1ve+rV9vrCw+5DXcTlpbWTiu8AvrFL2obI02goG6jli+3wSE1NfY5HTDAVvgffmif+eOOszx65RX7/H7rW5Yxt95qjWSwhlP37vZd79PHGqYVFdYjUFEBP/qRNYZ27LBMyMiw/Bg3rvFbg+1GOLRTUhp+zKpVFqrhcfRh3rfcztOHH4ZevWxT6mhKSuzNLy210UKN3vQ6zJYtFrj1dadUV8Nrr9kKsX9/WxGABfKjj9rzhg+3raBwF9pbb9lrGDy4cfN/+23rW7ziii9/UMvLbd4JCfbhDx/DcDQ1NfbF6d7d3sOaGlt55ebae3/BBbUr8GOgoG7n9u+3hls4B8rLbct87Vq7FBfbdyMvz/ZDxsTYVl5VVW0XJFhDbfdu+96kplqD7PjjrXGWkmJdxs8/b1vb48dbAychwRpga9bU9tF36VLbE9Crl61kSkqsIdS5M3z72/X3sIi0ZQpqOWYFBbaVnZZmYbxnj43Omz/ftth37bL9itu3W2PxlFMsxBctqu2qLi21LcVu3WzL82hOO822WLdts/19WVn2NybGGjMDB1rIx8XVdgWmpdljwrZssRVMp052CW+JlpfXNozmzrUVw1lnWQOuosLmOXCgRgZK5CmopUVUVlpAZ2VZ+H3+uW3RO2dbt7Gx1irfvNm6VTp0sDAsK7Ou5bIy6zbctctWAl26WDfhbbfZ8/v2te7BrVvteUfTs6etKHbutB2xdXXrZuGen197W7nUdBUAAAi4SURBVExM7dZCp04W4lVV1p08cKB1g48fb12cmzfb1kJ8vA0Y+fBD2wLp0+fQrszhw21ETufOVk94q9t7u8TEWHfo+vX2vF27bOUwZIg9vqzMbq+stNsrK22rIyur4dftvT2usVvwEkwKamnVvLdulJoaa+F/+qkFfVWVBSRYl82KFdbNGRdnY9G7dbOwLSmxgC4ttS7EhAQL5smTbZpvvWVdmikpts9u3jx7TkzMoYE/cGDtPqkOHWxa27bZPGJj7fnFxbWPj4+3Pv39+216lZW1w9eb6vTTrSs3NtaOd9q8uXZLp7DQ5pGdbYHeo4d15WZk2MrnzTftMcnJtuLp2dO6vMrKbKV0zTW24ti82abRv7+tQF55pXZgSYcOtuKMjbVlNWiQdXtt3mzLtWtXew/S0w9dqRyt6917ey+PYd9bm6OgFjlGmzfbyiE93QLswAHb1zZ8uK0IwMI+3Fpeu9bCvbTURtpt22at6/BQ3F27LEBPPtkCvnNn29+2Zk3tKLLduy0Qs7Ls/48/ttZ8bq7Na8wYC+KkJGudp6dbUK5fb2FZUGAjE8NbCwMGWKju2FG74omPt+eXlFiA1x28cCTh0UQxMbYVsHr1lx9z3HG2Et2zx6bbo4e9/vD5x8KXffvsUl1ty+T44+36sGG2cnjnHXve8cfbiLnSUlvBDhxo9RcX2+tOSLAVUkWFLa/jjrNRc3v21B6TkJZml/C+w8JCm0aPHjavN96wrbnw1tD27ba1dOKJ9j4sX24rtsGDbRrFxfaczp1t+ps3W52jRx/7/lcFtUgbUFFhrfLGBEFFRe2O3169am///HMLvIEDLXQXLrQdxqedZuGWl2ejAWNj7Zii8nJ7zoEDtiVTUmLH4CxcaCusc8+1QNu92+aTl2fdQsnJFqJJSRZ64a2OupeOHS3okpJsgMbnn1vre+lSm8+QIfa8bdtsJRneR/LZZ7X7H/btq31tHTrY8qkbaXVH+x1NQ1s7hw9jT0216R0+tB1qt6qOZWe4glpEWo2qKgv+8FkCKisPHWF34ID97dDBHltVZddjYuy+zZtrz3k2aZKtECoqLECLiux6jx423fDWx4kn2gGwK1bUHgn8+ef2/8aNNgoqvNWyfr2F+gUX1G4d9O1rtxcUwNVXH9vrVlCLiAScfoVcRKQVU1CLiAScglpEJOAU1CIiAdeooHbOjXfOrXfObXTOzWzpokREpNZRg9o5Fws8BJwDDAUudc4NbenCRETENKZFPRrY6L3/1Ht/AJgLTGrZskREJKwxQd0bqPM7S2wN3SYiIhHQbD8d7ZybBkwL/bvPObf+SI8/gu7AzuapqlmprqYLam2qq2lUV9MdS23HNXRHY4J6G9Cnzv9ZodsO4b1/BHikiYV9iXNuSUNH50ST6mq6oNamuppGdTVdc9fWmK6Pj4CBzrls51wH4LvAS81VgIiIHNlRW9Te+yrn3I+BV4FYYI73vp6TG4qISEtoVB+19/4V4JUWriXsK3eftBDV1XRBrU11NY3qarpmra1Fzp4nIiLNR4eQi4gEnIJaRCTgAhPUQTmfiHOuj3NuoXNujXNutXPuxtDttznntjnnVoQuE6JUX55z7uNQDUtCt3Vzzv3LObch9Dc1wjUNqrNcVjjnSpxzM6KxzJxzc5xzhc65VXVuq3f5OPNA6DOX65wbGYXa/uCcWxea/3znXNfQ7f2cc2V1lt3sCNfV4HvnnLs1tMzWO+f+PcJ1PVunpjzn3IrQ7ZFcXg1lRMt9zrz3Ub9go0k2Af2BDsBKYGiUaskARoaudwY+wc5xchtwSwCWVR7Q/bDb7gFmhq7PBH4f5ffyC2zwfsSXGXAmMBJYdbTlA0wAFgAOGAMsjkJt3wbiQtd/X6e2fnUfF4W66n3vQt+FlUACkB363sZGqq7D7v9P4NdRWF4NZUSLfc6C0qIOzPlEvPcF3vtloet7gbUE/5D5ScAToetPABdEsZazgU3e+83RmLn3fhFQfNjNDS2fScD/evMB0NU5lxHJ2rz3//TeV4X+/QA7oCyiGlhmDZkEzPXeV3jvPwM2Yt/fiNblnHPAxcAzLTHvIzlCRrTY5ywoQR3I84k45/oBI4DFoZt+HNp0mRPp7oU6PPBP59xSZ4ftA/T03heErn8B9IxOaYAdEFX3yxOEZdbQ8gna5+4arOUVlu2cW+6ce8s5Ny4K9dT33gVlmY0DtnvvN9S5LeLL67CMaLHPWVCCOnCcc52A54EZ3vsSYBZwPDAcKMA2u6LhDO/9SOy0s9Odc2fWvdPbtlZUxlw6O3L1fOCvoZuCsswOiubyORLn3C+AKuCp0E0FQF/v/QjgJuBp51yXCJYUuPfuMJdyaIMg4surnow4qLk/Z0EJ6kadTyRSnHPx2BvwlPf+bwDe++3e+2rvfQ3wKC20uXc03vttob+FwPxQHdvDm1Khv4XRqA1beSzz3m8P1RiIZUbDyycQnzvn3FRgInBZ6AtOqGuhKHR9KdYXfEKkajrCexf1ZeaciwMuBJ4N3xbp5VVfRtCCn7OgBHVgzicS6vt6DFjrvb+vzu11+5S+A6w6/LkRqK2jc65z+Dq2I2oVtqyuCj3sKuDFSNcWckgrJwjLLKSh5fMScGVor/wYYE+dTdeIcM6NB34OnO+9L61ze7qzH+3AOdcfGAh8GsG6GnrvXgK+65xLcM5lh+r6MFJ1hXwTWOe93xq+IZLLq6GMoCU/Z5HYS9rIPakTsL2nm4BfRLGOM7BNllxgRegyAXgS+Dh0+0tARhRq64/tcV8JrA4vJyANeB3YALwGdItCbR2BIiClzm0RX2bYiqIAqMT6Aq9taPlge+EfCn3mPgZyolDbRqz/MvxZmx167EWh93gFsAw4L8J1NfjeAb8ILbP1wDmRrCt0+5+B6w57bCSXV0MZ0WKfMx1CLiIScEHp+hARkQYoqEVEAk5BLSIScApqEZGAU1CLiAScglpEJOAU1CIiAff/eU+GcpDrDyEAAAAASUVORK5CYII=\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ },
+ {
+ "output_type": "stream",
+ "name": "stderr",
+ "text": [
+ "/usr/local/lib/python3.7/dist-packages/sklearn/manifold/_t_sne.py:783: FutureWarning: The default initialization in TSNE will change from 'random' to 'pca' in 1.2.\n",
+ " FutureWarning,\n",
+ "/usr/local/lib/python3.7/dist-packages/sklearn/manifold/_t_sne.py:793: FutureWarning: The default learning rate in TSNE will change from 200.0 to 'auto' in 1.2.\n",
+ " FutureWarning,\n"
+ ]
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEICAYAAAC6fYRZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOydd3gcxfnHP7N7VadebLnLDVdsMDZgqsEmFBsSEkpCC5BQDCmQ0AL8ktBS6IFQAoReHTqmNxuwce+9yLZc1Pudru3u/P7Yk3TS3UknWXIR+3kePz7tzsy+e+W7M++8846QUmJhYWFh0TNR9rcBFhYWFhbdhyXyFhYWFj0YS+QtLCwsejCWyFtYWFj0YCyRt7CwsOjBWCJvYWFh0YOxRN7C4gBCCDFHCPHr/W2HRc/BEnmLgwohxHYhxLT9bce+QAhxqRDiu/1th8XBjSXyFhYdRAhh2982WFgkiyXyFgcNQoiXgIHAB0IIrxDiJiGESwjxshCiUghRI4RYLIToHSk/RwhxlxBinhCiXgjxmRAiN6q9o4UQ8yP1VgohprRx7e1CiJuFEKsAnxDC1lb9SC+8MHLdbUKICyPH/yqEeDmqXIEQQrZ+cAghRgFPApMj91rTJW+ixQ8OS+QtDhqklBcDRcCZUspUKeW9wC+BDGAAkANcDfijql0AXAb0AhzADQBCiH7Ah8DdQHbk+FtCiLw2TPgFMB3IBHonqi+E8ACPAKdLKdOAY4AVHbzX9ZF7+T5yr5kdqW9h0Ygl8hYHO2FMcR8mpdSllEullHVR55+TUm6SUvqBWcBhkeMXAR9JKT+SUhpSys+BJcAZbVzrESnlzkhb7dU3gLFCCLeUslhKubbrbtnCInkskbc42HkJ+BR4XQixRwhxrxDCHnW+JOp1A5AaeT0IODfiaqmJuEOOA/q0ca2dUa8T1pdS+oDzMXvixUKID4UQI/fqLi0sOokl8hYHGy3Spkopw1LKO6SUozHdIjOAS5JoZyfwkpQyM+qfR0r5jySv3WZ9KeWnUspTMB8aG4CnI/V8QEpUO/nJ3quFRWewRN7iYKMUGNL4hxDiJCHEoUIIFajDdN8YSbTzMnCmEOJUIYQamcCdIoTon6QdCesLIXoLIX4c8c0HAW+UTSuAE4QQA4UQGcCf2rnX/kIIR5I2WVjEYIm8xcHG34HbIy6SGzB7wm9iCvx6YC6mC6dNpJQ7gR8DtwLlmD3zG0nyN9FOfQX4A7AHqAJOBGZG6n0OvAGsApYCs9u4zFfAWqBECFGRjF0WFq0R1qYhFhYWFj0XqydvYWFh0YOxRN7CwsKiB2OJvIWFhUUPxhJ5CwsLix7MAZVoKTc3VxYUFOxvMywsLCwOKpYuXVohpYybkuOAEvmCggKWLFmyv82wsLCwOKgQQuxIdM5y11hYWFj0YCyRt7CwsOjBWCJvYWFh0YOxRN7CwsKiB2OJvMUPivKaeuas3MquCmujJYsfBgdUdI2FRXcxb802fvvYuy2ODeubyws3/xy3w56gloXFwY8l8hY9nov+9iLrdlbGHN+yp4LTbnkKXzCMNCQDe2dx3xXTGdavrR0ALSwOLix3jUWPJaRpHP3bR+IKfCP1/hCGIZHAjtJqfn7PK5TXePedkRYW3Ywl8hY9lt88+g4hTe9QHUNK7p01p3sMsrDYD1gib9FjWbJpV6fqrdle3MWWWFjsPyyRt+iR7M1mOP1yMrrQEguL/Ys18WrRIxFCkOFxUesLdLjuH845sd0yJZV1XPnwm+yqqEUAJx02jPuvOrMTlu4ds+as4OF3viUQ0hACCnplcdYxYzjliEPoaz2sLDjAtv+bOHGitBKUWXQV89du4zf/frf9ghHsqsKtF0zjx8eMabNcSWUdZ9z+34Tne2elcs/lZzBhWL+kr90Z/jd3BX9//euE56884yiuPvOYbrXB4sBACLFUSjkx7jlL5C16Mqu3FfPLe19PeP7m80/i5MOG4QuGKOidnVSb0258kiqvv91y918xg5MnDE/a1o7w2ZKN3PLfj9otd87xh3LrBdO6xQaLA4e2RN7yyVv0aA4d3If+uYndFqdNHEleZmrSAv/sJ4uSEniA21/4JKlyHaWyzsdfXvw0qbJvfruaZZs7NwFt0TOwRN6ix3P7RfF7ssePHUxGqivpdgzD4IkP5iddPhDS8AfDSZdPlq+Wb8HowAD85S+XdbkNFgcPlshbdBu7ymuYvWAd89ZuR9ON/WbHkSMG8vjvfkp+VipCCJx2GxdPO4J/XfuTDrWzs7wWvSPqCthtaofKJ0NI0zsUPbR88+4ut8Hi4MGKrrHoUirrfHy/bgePv/8dJdU+XA4bqqLgdtp56rpzKMhPzi3S1Rw9ahAf/e2KDtWRUnLfrK+ZvXA9KU47vzp1Uoeva1O7vh91/KFD+Pd735HsOq+GUIh/vzePt79bhaYZHDe2gFsvmEaq29nltlkceFgTrxZdxitfLuOBN+fGPScEDMjL5J2/XooQYh9b1nGKK2uZfvuze93O0sevS3i/UkpWbythW0kVu8sqePnLFRw3poB7r/5xu+3+58PvefaTxYSTUHqbqsSMpFKcdj7/51W4nVZytp5At0bXCCFGAG9EHRoC/BnIBK4AyiPHb5VSthkOYIn8wcvGnWX84m+vtFnG5bDx8i0XMKRPzj6yKhZNMzAwcNjaHsROvOahDvm943FI/zxev+2iuOd8gRAz//UW67eXEE+mrzljIr8+8/g221+3o5TZC9bx5fJNlNc2dNi+IfnZZKU6Wbql5QrfGUeN4q+X/AhFsby5Bwttifxeu2uklBuBwyIXUoHdwDvAZcBDUsr79/YaFgc+73+/tt0yUkIg1PUTkbHXkfztlS94a96apmND+mTREAhTUm0mH0tPcXLvlTM4csTAmPo1Xv9eC7yqCP7085MTnn/wrW/YsLM0rsAjJY9/tISCfr2ZNuGQhG2MHtSb0YN6c9P5J3H1w2+yaOPOmDID8jLYWV4bt35hSVXc47MXrmdrSQWv3BL/AWVxcNHVPvmpwFYp5Y6DYUhu0XWUVbefuTEY1hjWt3vS+O6prGVXRS3Pf7KYBRuKYs4XFle3+LuuIcjMh9/i7stO4+G3v6Wi1oeqKpwyYTi/+fGxnbZDCBg3uA+3XjCN4f1yE5b7eNF6ND3BkyTy27np6Q+ZeWYVV5xxdLvXfex3P+WZjxfy2lfLqWsI0j8vg9sumMayTbt4+uOFHb6P9TvKKa/xkpeZ2uG6FgcWXS3yPwdei/r7N0KIS4AlwB+llNWtKwghrgSuBBg4MLZXZXFwMLx/Hl+u2NJuuS17yhk9KL/LrltYXMmNT81md0VthzNOSuC255pj2TXd4OPFG1mwZnOn7fn8H1eSne5pt1xYSy7a6KnZC5g6uoAhBW2/Z6qicNX0yVw1fXKL42MG9uaZTxbSGa/sgvU7OHNy26t/LQ58uszpJoRwAGcB/4scegIYiunKKQYeiFdPSvmUlHKilHJiXp61WcPByplHj263jF1V9toNEk0gpPHrB2exvaSqwwLfRBz1q/Z3LtwzPcVBiiu5iJWjRiXXodGDYS477jbuuvmFTtmUmuLk3l/PQOnEyPpACsqw6DxdObNyOrBMSlkKIKUslVLqUkoDeBo4sguvZXGA0ScnnVMnjmizjNvpYNTAXl12zbkrtxIK63RaiqRsco10BXUNIY75/aNc++jbGEbbD4pbzj8Jj9Me9yHTAkWg1geZ+9BHzPlyRafsmjphOIv+/Tv+cE7bE7mtEYrlcu0JdKXI/4IoV40Qok/UubOBNTE1LHoUd116GteedQzpKY6Yc067jfuvmoHahREb5bXepN0ecemmeaPv1+3gxqdmt1mmf14mH97zKwaneUyhb/wXjW5gK/Wi1gdBN3jxwQ86bZOiKFw0dSI/OiLxRG5rhkZFQdX7g7wzbzVn/+W/TJj5EBNmPsTUGx9nfVFpp22y2Dd0SZy8EMIDFAFDpJS1kWMvYbpqJLAduEpK2eZuDFYIZc9BSsmSTTtZtGEnOekpnDppJFmp7i69xsrCPVz90JsEO+uq6UYEsPSJ65Mqe9ZRN1DVEETPcBEanodUFRAC+55aUr/chBLSCRRk4ps6AtVh41enTmJ0QT6DemczqHdWh22bvWAtT3zwPcVV9XHPKwLGFuTz/E2/AGDl1j3M/NebBMLx3+fX/nQhI7pwhNaaVYV7WLJpB0P75HHCuKEHxTqLfY2VhdLioMUwJGu2l+ALhBg3pA8eV/MoQUrJT+94gR2lMfP5BwSLHv09NlvsyEU3DNZsKyE9xcXgPtkEg2H+efvLfP/6fPSwRjikoQTMfwCVv5wEzkiMRCuB65WZymu3XUhWakqH7QuGNeau2sotz8QuX5lz39Wkp7rxB0OcdMOT7c55fHXvVWSmddyGRGi6weX3vcqaHeUx56aMG8qDM8/qsmv1BCyRtzhg0TSDuoYAmamumMU3hcWVnHvniy187lMPH8Z9VzZvznHd4+/yzept+8ja5FEVweLHros5fvqtT1Fa7Wtx7NVbL2TkgOae8B9++TCrXvseNIOGw/oROHJgm66l3lmpfBwnZUNFrRebTSXTk3gEdeS1/0JLMH+w7Inruenp2XyxrP1oI0UI5j4wE0+rVAm/e/Rtlm3dw9TDhnLHpae32w7A7ooazr/rJRpCWsIyvz/7eH75o7ia9oOkWxdDWVh0FF3XufPlz/ls6SaCEReAoggumXYEvzvbnBw0DMk5d74YU/fL5Vu4742vufH8kwBw7edl+Yf0y2PT7tje5kVTJ8Qcm/KHx6nzB2OOX/C3V3jrLxdzyT9fxxcIQwoovzoaQzdM30k7lFZ72VNZ27QT1Ncrt3DDkx+0eDjOnHE0V7QKr5RSJhR4gFe/XMzXy5MLJzWk5PbnP+GhmWZKho8WruP255vTIX+wcAMfLNzAizeew9ghAxK2s6qwmCsenEW4nYR2j78/zxL5JLFE3mKf8dSHC3ju00VNwh6NYUie/2wJZTX13H3ZGTz+wbyE7bw2ZwWfLNlIdZJ53bsDl13l9z89nvOnHM4Lny3hqQ8X4A+FEQJGDujNZacdFVMnnsA38rM7XmrxtwHQgeRmO8tMkd9VUcMfn4ydoH1i9gJe+3o5X91/TdOx9lww97/5XdLXB1gcteI2WuCjueS+N9vM53Pny5+1K/BAUmUsTCyRt9gn/PXFT3n/+3Xtlvto4Ua+WboFvZ0MvftT4AWQlZbCvW/M4d435gA09ZqlhPVFpUz54+P87ifHcWkkc+XrX3dvTveZj7zVbpkaX5Db/vsh9/xqOgCOLk6D3Jg7//u1bbvPVmzZzeHD+8ccr28IUFRWk9S1PC4rsVqyWBmILLqForJqbvzPB1z491e59/WvkxJ4AAR4NQ1/MLE/dn8jgeKqemTkdaJZrUfe/Y6GoNl7X7m1ZB9Z1zYfL9nUlJGyq6fjJDBh5kO8P7/taOndVXVxj9vbSRoXzT+vmN4R037QWD15iy7nw4Xr+b/nm9MFdDiWWohI3Dhmt/kg5vQ/PU29v/uTsnWEGq+f3AwPx133aLe0/+myttNbjBvcJ+5xl8PGCYcO4ZvVhW1uMnPbL07mmNGD98rGHxJWdI1Fl2IYkqN/+0ibE3oHLj3gqXKAYFcE4QQ5LI4bM5hHfhN/V646X4BrHn2bbcVVgMQf0rCrCiMG5PLItT8ls4vXWvQUrOgai33G6m3FB57Au3VQJXhVEot4os6OJfyd4aWbfs7P//Fa3HPfrd2GtyFIakpsnp90j4uXb7mA9UWl7KmoY3j/PAb2yuxuc3s0lshbdCn2OIt/9hspOuqkWkjTQYKssWHMyyS+aEtzhsogwXmLjnD5A2+0eX7j7nKOiDP52siogb0ZNbB3V5v1g+QA+kVa9ARGDeyNw971m1d3HIl6bA2k6wgVhA3w2cwefVxEgs58TxL8feOatSmChnDbo7ny6vgpFSy6HkvkLboUIQQPXt3GknPdwFZSj1ru7frwjmg78sJgl4job7irLeERIAU9S9T3D1oS+aRvfe4TJsx8iBc/7/gc3JyVm/nlP1/h25Xt719gYU28WnQTK7bs5vIHZrU4Zt9ZTeoXm5oiZ6TTRv2pI9Hzun73IdE/gDLOi7A3f7+lAfrn2RBQSOiyMWt3uT0WifnqvquTmlCtrqll6p9iN1efe++vSUtL6w7TDhramni1evIHCfNKvuSdrf+lrCH5cEQpA8jQYmR4/T7fAKJfbkaLvxVvkLTPNqKEdJSwgaIZqL4Q6bPXQjdkkZTVdlBa3rNQQJlcA/Y2XDaWwO9zrv6XuZArEAhxwvX/bkpl/NBbc1uUiyfwACfe9Ey323gwY028HiDous6ts2bzzdJtSGDKpMHcfc50NtWuI1B1NYenVKG5FJTqB3huy/FcNu4/TXWDgRXUV91EGkVIDGyidcoTG6j9IOsZhG3QPrmfvMxUHDa1aem8Y1M5cbeFkhLH9mpCwxLvh9opfCpylxP6BU1/PCB1052Ebgn5gURJVR0L1+1g5qNvtzj+0hfLePvb1Xz78G8IH4DppA8WLJE/ADAMgxNvfYyGOo3GnuRn8zczd8eDXD75e6ZlB3GlGkRCPzgv5xte3Xg/F4y4gS92vsdHRe/gN/oz3uPiV/kb4vRFNQxtB0blRdh7zUWI7h/A+QPBFrlRFH8YEUfkhSERwe5ZLGSsSENUORAFfoRNYux2Ire6wbBE/kDCHwzHCHwjvmCYbXsqyEpvO41xKBTC4YjdrMbCEvn9hhYqorbiUjLELtbs6oVWfya20gAUBJEngayxE1yaxhNvHMcTUqCmhTn5lPVcP3wZbkXD1zCXc77axuGpFVzffyPpagi3oqGI+FlpFQF+rZItFR8wOu/H3X5//5w1p8Xf4f4ZuDaUImJ2chJofTLoHgSyyIUscnVT+91Ao1vtB7QxRnvJxs69+yU+uPPyNstYAp8YS+T3A4bRgFH5IzKFgRDwypsFeJ5bgRAG4UluGib1xViYATqIXkFEQQApJN+uGMy4vDJOyy7i/F5bOT27iD4Of5MetLdlqUDyzo7PGJV7VrfvrhNo1TsPD8hCy0tFLfeiRIRe2hSCQ3LQs7tus4mDnsaUDhZNGBKm/198fzxYsyjtYYn8fqCy6m6yMQW+uNjBolVOQtelkDsgxNFj6zkmeyHVI508VTKaBhwR4ZY8cuwXjPFU4VRMkfQoWgtRb0+3HYrB/NoUqkJecpzdG41w47kn8Vn0ZhOKoG76aJwby3BuLkeqCsGRvQkNzUncSFfQxZt17xMONnv3M9OPHMmt//2I86aM57Ch/dotv72kiqr6BkYM6NVip7GeiiXy+xApJW/vXMQzm0JUaz8lxxagzmsjeK0NxQZ1ios5/kzm7u5Prt2PLpSmXsrolGpGplQ3CTwkpwXRncL5tfnUaC7cavd/sXMyPRxakM/q7VHZF1WF4Oh8gqPzu/36Fj8cZi/aAMAnSzZy5IgBPPH7n8UdqVbW+fj94+9RuKcSm6oQ1g2uOXMyF5/SszcfsUIo9yHPbPmSf657j0rNgYFCuZZCwGkHm4KBgt+wE5IqQWljdyiVUNQzeJirttPD0u0bnYSkwj93HclxvUaSYovNGdIeUkqkUYuUoaZjujR4ffN8Tnv+IaY+9QAPLPyYoN7spnnh5l9w6y9ObrPdUQPzyG1nUm2v0PQfnvvDkNh3VOFcV4Ja6Wu/fA9i0cadzF4QP631H554n3U7SgmENbyBEMGwxkNvf8sjb8/Zt0buY6ye/D4irGs8vfWrmONmjyNeEqyWf+8KeTA6IfPBAHz6RhaFlwxlUPoh/N/Yn3W4DRn8Dln3Z9BLAAXpPguR/mcuffdF1n7ZvDz9lZXreWf+GuZe90fUSATPOSeM52+vxd53I8eNHcyQPjkcO2YwAjj+D4932L42samdc3+4dZQRPkRuGBlQkJtTkKUdfzi2YB9Mqip1AdLfX4MIaQgDEBDqn4n3lBFJbSXYE3hy9gLOnDwGgIXri7jvf1+zp7KOQII9Y5//fDk/mjS6xT67PYkuE3khxHagHtABTUo5UQiRDbwBFADbgfOklNVddc2DiYWVbS3Bbv/Ht9ybR2nIzQCnF3tkkY8h49ds1JBwCFbNT+XdD/rw9H33Mig1r8N2hwJr+G77HWwLpFIeHktF2MUA5waGOmew9qvTaL2FU8NWldtnv8ffzzy76diwPtlsKa6K2/7THy1qen3MqMR7f3aaTgq8OqUabGZaBOExkBl1GOs8yG17MeoQAuENonqDaPnpnW+nDVIWbEc0hFAkGCl2pKpg21WDa20xgUP7dss1DzSKq+o46YYnuPSUCfzr3flJ1bngb6+w7Inru9my/UOXpTWIiPxEKWVF1LF7gSop5T+EELcAWVLKmxO10ZPTGszevZQ7V7e/RVsjKjoSgRHlUctQg/xpwFKOTS9GCFjfkMULxcO5LH8jBU4vfz6/P6dfUMPoiQ3U16h88HwOX7yVjRzam883PNYhe6WUPLv1a17f9iEhqeA3GvsDAhs6dkVye68lPPvNBDZnekCRyG1u5B4Hat8wd532YyrLaynzBhg3vB8PvjmH4ipvh2zoONHf5c73WpXx9YiBAVovJ5Aa6B/n7l2cvT+MUAXS0dn+VRupj6UEzYCwjhLQMNJdICVKUMO9qAjfycM7a/UPhjOOGsXdl562v83oMPszn/yPgSmR1y8Ac4CEIt+TGZne/qx/4w/YJTRGuavIsvn5qm4gjT/qWt3JLduPwSYMVAwCuo1JOUM4dJi5CfTkCz/m3t8920LrjAwXj826scP2/m/H9/xnyxco2Fs8aAA0VDQD/lwyiUPG16D6bUgUZE49BEBfn8Kt774PVXbTlq+Wg4C8TA/3XXEmizcW8dj7yfWwkic674wEEdlZqhNiL3JDMQLfdAmPDvWd/NnoBmqtHz3H07n6pnWmIQIzbYMqIRQZTQkBdhXsKobb3jSKMewqvhOGdP6SB2OEUif5aOF6/MEwD1x15v42pcvoyolXCXwmhFgqhLgycqy3lLI48roEiEkQLYS4UgixRAixpLy8vAvNObAYlpZPlq29ob7ALcL0c3jZFkznq7pBNItU846imhQENBvjUwbx8KRLm2qfd+3pvFvzPEdfeTL5U0Zy3G9P5YNdTzFqXEGHbH17xwLu3zAbkDECH42Oynp/DjJioxCAC9RDGxBDGhD5QfNg5BbKa3zM/NebbC+N77pp5JjRHXXbNPZuG9+rSNpgR+c2L5H+BKmSFSDYgZ+MlM1++LAOAQ2hG6YQ7xUC0jXUybWIMT7iphBuLcqKFWORLF+v6FnZLbuyJ3+clHK3EKIX8LkQYkP0SSmlFELEfBullE8BT4HprulCew443jvpJk74/K8Jz0sJDWE7W/TMOD1JyWGiipLSbAZ6xvGXaWeSlxEb656a5uHuJ2d22sYPdy/lvg2zI38l23trLicESBuIkAIFAWSJs8X5QEhjyaZdbbY2vH8vHrz6J3y9Yit/evajjt1AtE0hBQwjInCND4L2XTpycwoyq7Yp5w2YeW9kmcNsMykivV/dwLanFrW6geCo3ubq3r3uGUtEdhiRo0G1PbkqezPp+gPpxfdUukzkpZS7I/+XCSHeAY4ESoUQfaSUxUKIPkBZV13vYMSlOnj5mN9y2fzHCEfy0ERPichagfAYzTG+Ue5Xt+Lkj0f/lRHp3Tt59uTmL9Dl3m3fJwTQO4T+VXarMxIJlFa37Zu/9szjsNkUJEnY0Z5gNr2/UWXyQqY4aglEvtyOsToVZazPdPsIkKUOjGUdmCxtfJ5IcGwpw3/MkC7owTe3rRQEkGEBqQfWJuFNSGk+4Iqq0QZmQ/SOYVJC2AC7sl8eIE4Vgj+gfGddIvJCCA+gSCnrI69/BNwJvA/8EvhH5P/3uuJ6BzOHpPdh3ml3s7m2mG/L11MaqCPHmcq03FRKq5+mPriDObUDWFLfh4C0k+1M48x+E7hw8HG49sEiprJAbZvnpQHGZjeyMMUUyeww6lgvIqP5VyMloAJ6Yw+6kbbEOFJO05ly5QM8e+el3PbsJ0laHX8yUiAZM7CMNbtbLb7y2lCOrTHz2iSIlpFFbvSdLtMHH1QgnLy7QxEGttwgoXI3qILA4f2RXbktoktHX50KlY29+AOwpy0EqAra4Bwcm80MpKGRzd5aW0kthsuO0avrVl4fNrQvO0qrGdQ7i5vOP4lvVm3hydkLW5RxqArf//v3AEz54+PUNQRj2umduTdzJgceXRJdI4QYArwT+dMGvCqlvEcIkQPMAgYCOzBDKBM6ZHtydM3BQHmtl+nz/9amZujLU5G7nREBBzAn/9STqhGe5p639Cvon7WXskA2/xfdozOk6cN2ttMHaerFRwLC4xh+/pGr2FSSy/Ki6BGQabNyXA3GyjSoSdLlAeZEZ0bYdNt4FWKntSQj+5Rz0rEbeeLN45NvN2kk2GRkFNLqfqWMxNXG5Jrev0iJ8AaRbkdzj14zTFdap6OMYokOgbzygddZsqW4xflZt1/IsH7NsfCBgMbUm5/AHxU/n+Z28OW9V2GzHVxLiLo9ukZKWQiMj3O8EpjaFdew6F62e8u49MNnkFmJNV4GBHKXq1UIoQADjC0pqOOb3TDSm7jnmp9RxwPnf8Ih+ZVc+NQ5bCppFb+vCHAk4dpoejAoiIgrKBq3I8SRQ3YxsWB3K5EXoIOxyYMY6EcmK/L9A6jj65FhYW4IrgiaPUoSRRicM3EtN50xj0ue+SlthjvuDfEEPpp9oe8dWdglBDK11UIymxLZbrFrcNpUarx+bn/uY+av2xG3zHl3t4yFd7lszPvXb9ldUcP8tds5/tCh5Gf3vB2mDq7HlUW3sK52F1d8/x/CWXrbv1mvzQzbax0nLgWypvmrJCXInfHT+3qcQV789VtkpgQQAooqM+Nfq4O+2nR3gKBmIxC2R6ob+EN2bnvzFI4dHu9HL6DSZvq1k0IiXDrCBsZ2F/jVmIedqsA1UxdRUZ/C5pIcukxtWwhqW+IuQE0yJene0tG2uzm75nt3XM70255p0SuPx9fLN3HS4Ye0ONYvN5NzTzys22zb31hxVT9wQmGN2+UFvjMAACAASURBVL57lTB6k37IROlePHr8hUBCItLNH5c0QFbYzO334jB93EZSHOGmiL78jK5ZIBXSVK4/ZR4j8stRhBGxXxDQ7MzdOLhlYZcOOSFzY++KZF01oim0UpY44r4PUsKVz5/FOY+dR1jv5CSrISGkme6MkIZaXIdjQ1n8XbXaa+dAy9nT+sHQRQ+hw4f15Y1vVrQr8AA3Pf1hl1zzYMLqyf+A+XL5Zu7647M0/BEaFV7f6USu8aCeFjt1ItwGIj9ohkVGi5wCyjA/stKOvijddGEkiFwZ3bccl6N5knbmSYv4y7snN/XAAVOgdMMc0icpBEHNxk+O2EBdwMX2ikyCWnN7mtG4WEiiTKhD9AmZ9qsSuduJsTytfdeBkCh5ZiSLcBoR51DLOpqhRlxPnRevtNlrkE47an0QW6UPLcNF7fmHd1wQE+0e0wPplZnGd6sLkyqrH2DPvX2BJfI/UHaUVnP7k7PxfFuIuLoAma4i61TkyjRzD9QGgUyRsWtqJtRjrDOQO9xmlqJUHeXQenAZ6HMzoyZk47O9IrOFJ2Hq6EL8IRuPfnE0lfVu3AuLcK8rAd3ASHXiO3Yw4UGtQzFjUSJLMNYX57UQ+BZlRvkQ+SGEijmBCtAniGhQkRvaiagQEvIDZjtDAuilTvP+Ywu2a2tbNBwxkJSlO7FFskf6ju7knrwHgsDvo5Wyny7ZiF1NzilRkNc9OYMOZCx3zQ+Ut79bDburkYrA8X4NhA3T1xwRLn1jfNETKqiH+lBOrYDcMPhV5B4nxrqUpCbSXpo/nmqfs4UnYfr4TTz/q/fwfFuIe10JQjMQEtT6IGlfbMJWUtdcOIELQjNU1u3J45D8Cpy2eMN2iSgItFjgBCBsoAz2t2s3hkCEFaQGIieMGOU15yfirTbdC/S+6dTPGINvkrnq18h0JxbK2LWFBxb78EHT3haCjfxq+jFNr32BEKsKi9lTWRe3bFjX6arcXvsTqyf/A6WizoduUwGJ8/Uq9Fwbek4GTT3R3S4Y5435hkgD0AVyXUqTP9vs1Ud8+jERhS17c7q0ceoDl/LMZe8ybmApSPh6/TD+8toxuDevQrQeT2sG7sVF1M8YY7px2ggNvOeDKdx//se8PP8wQpqCJCrME8zQw3gkOt4CgT43CzHYb44GUgxkZhiqunjtQiQNRGB8P1zryxC+EGTEEXq3ZoZx6q3fDxkbktoa3TA/l8be74HQ6weQErXCh5ASLTe1y8NAL5o6gTOOHAnAs58s4umPFmJXFcK6zrghfbnnl8dzzp3/oy7QcoHZTedN4fwph3X7lpndRZdloewKrDj5vafIW87L2+ewub6cUem9ubS/jVx7CBxTUGzNoYqfLN7AXS99jvPZ71EawgggcGgvfJOH0JhTQQzyo4zzQiv3rvQqGDtdoAlEfggcBu4HyvGNGxa7qrMNYb7hnOMpKarg5e/XotYFSH9nFUo4tkcmBVRdepTpo9f0NmOrc1J9TB1VyLIdfdhalhORd/P6ygnVKFmxvXyjyobxbVbCNruMxjj2ZFwLUuJcV0JocA4yJc6DxGaYtxVuFXEjZJsjKuELkfXaUtM5rQgCI3vRMHmwGZWzr0UsqgOglHux76klPNhcW+HYVEaoTzpGvwTRV0nwzf1XUlzjp6zGy6gBvciObE7z1Yot3P7cx63yy7fWwZbvxc3nn8T5Uw7cCJy24uQtkd8H1JTX0lDnJ39wLxRFobLOx/LSHazVdlAWrOHQzEHM6D+BVFv8sMNkMIwQJcU/JxDejk1IltbncWLmHuzCwKVoZmSdczpK1kMAhDWdy+57g21ri3C9s8oUT0Whfvpo9LzU5q98VhBlvLd5oVOcPThEcZi0mTvwHjeMUEF2s9CHddSqBvTeUbHH2SGUQQGwS/oH7ZQudxJUVAjrZL+w2Ezg1QoJNBxTQGBsH9zLduEf17fNFAG2snqcq4tBNwhM6G9mfRQCMsOox9aAYj7HGr/6eqET1qaCTJR6sovEL6Rj31xGeHR+8oKayK8tJMqxNWaqhaBoWgumTKjHWJie2GZDkvLdVtzrmzOM+CYXEDi0D2gGju1VKIEw4b4Ze5ktMwka7y2so9b40bNSmkNANQNbhQ8txW6OZDrJ0sevi+mBX3rf66wqLE5QIz52BRb8O7atA4X9mWr4B80XS9dyx+dvEsgPo1YY5HxQR/ao4Ww8vApy/IhKDZlr53PPah7d+DH3TriIyTlmzm+lo1kDy04gV1QhIp2+Gdm+mA6jDH5ITbnElX0vTtXOTRefwH/eX8Cm7FSc87eRVhPgBCWF3hNHs7CqhpKGGsr71WDMy2pa1q+M8sIQfwvftlJuDm9Tv9pMaGgOwRG9AIFzUxlKjZ+6n5nr5MRwH8ohDU0PihIjiCe3juBXvcCuEhyUhbOwEgEYThuhwdlIm4pjZzX2nTUEDsnDvXQnhkMlOKp309L5aBwbykidV4ihCGrPOwzpak65S40d/csslBF+ZIaGSNfMOYYhQRgURBa6MdZ7aBZI2er/qB+4Ks3edFAh6YeAKnCvKTFFvj0iuV8Ac3ermLYkIltDnVYF9arptsnQ2rdHEfiPKsC1oazJpR/OS8VWVk/aR+vN1amRXn5wSA6+KcO6r4cfaddWWoeWlULKoh1IRWCk2FH8YYIFOTh21hDaC5FfvmU3E4b3b3Gsqq6hw+2EDdB0A3u8z+IAxxL5vcTrD/Le/DXMXrmGnaEKgiIIXpUU3U3DpFI4VCJU0HtB2ch0yjftQumvYhcS3WNnYH0NyqdetvxoINfPe470i7chfAbuVBcPzL2T4YcPbvP6mt7Att1XIjWNoVGu27gDNAmp2kfM+NKgSjd76yJbI+3VIgJ1BkFNMm97OY6PlnHjc7/hxHPP56Xl9/HwymaZMzZ6UNI1c9JVAjbQs20QMhMOO7dW4txaaV5OEfgP7WNWdBooIxrMyJbGthRBKBUzLLPYTXBcH5zbKgn1z6T+lBFmIQENRw3EVlxH6jeFCAmp87eTsqgI/dRRyGF5+IIhM4xcDZE6rxChGQTH90U6bbGukYANY2Uaon8AMcHculAI8z4Y6je9HRsiQq8YiCk1iLDA+NwDTgfYIpuK9I3kPAkJ5AIXRo2nXR+yCOvYav3Yt1WaEUPRtkV/YIbEM2cz9pJ6wn3S8Z00PFZoU3TQzYlj0s3ZcqmBsb79naukItBTndjqzXvQs9xkzVqBEooKFzIkzsJKfCcO7QKRj/OQjELL9iA0g4ajBkW+U4q5RqDGjxLauwRsC9YXxYj85NGDePu71egdXHtwMAo8WNE1e0VVnY/pf3mGB96ZwyZtF8HRlXCoFzm5Ft8hFeCQTaImFPMHKYfbMVSFoGJHEyq7MzKYfJGf+zO/wSYNwkeZQ2S/N8A1E28iGIhNoNRIYflLeIsnka8uY4i7ZYRA3BF+ZFR/Xq9CRnuqGOupxP1mFaJOR2jmF14akmBDiAevepI5O97k2Mx3OHLgLkTj+n1DYCzMRP8mE2OtB2WVm0m+iYh4USaGJDCyl9k7zAkRL6lkEJWCsabrQMtLRcv2mAIf2fwCm/lP659p5rMBDBvU/2gEdf3SqQ9EBB6J3V6FjNx4uF9G/B5w43uRH4x1O6mgHOJHHFcNdh0xOIiaZqBkaagT6kHXUY6qQfQNIlSzvHBLlMk+0r9fiWgIxb8YQFjHvWQnQkLa11uwb68yFzxpzcIqGsK4Vuwi69mFuLZUovhC2MsSLBars2MsT0P6FHOFsV/BWJWK3JlEr9emmJvH2xQMu4qt2t/CjiZ7NAP7zpr220uaBKLqtiPTXeZDrzG3jcOGnp2C4Uy8WE0IsLXz/MnwxLpA01NcHRb4v158SofKH0hYPfm94OZZ71PvDSIK/ChjG5pzwEugtxa/A9TqWFDaeLdqCL8avZZLbBt41RmVx0XCo9c+ww3/vTammUCohOzgP0i3Jd/TkRJ2BFI5J6+Qc/PMxSPXrhhGsRa7QbUv4Ofmt+ejbD4KpUxHcdahp5vRNw5VI+xVcbnD2MZrrPSso+99g6m6aXuL37EEZJrL/DUmWByFLgmt85uCZ1OomzE6of3BcfnYgl4axvY3Rb/VG2zUpiAiPWK1NoDWrzGXfMw7gVFpR+kXX5SFADEuKrOmEIgCHVvfSmSKEvu5OgShH2eQ8ehqas49rOVCJCFMP/i8QtwbzU1xhGaQ/sUmtBQ7DccMJjw018zvkmInOLoP9i0VhAdloQiDhuGJ/fdyjwt9j4sOzxsIQe25h6FW+syHu0xc37W2JKl1Cu1csF174mJTCQ9IPCEuJbz+50s4584XE5Y5deKIpte7y2v48Z+fi9PXiHf/zaOPXlkpnHXM2ITXONCxRL6TbKkvYenGXYhBoZYCTzuj2zjnfLqN/349CewGtuUte+4bF2+N28zGXVczxJl8b0RGIusGubwt7MvM0igmVuTRIPW2PaBLhCFxi1LCIzzUTxsBYUG/4ZWUjIwEd0jYPsaOeHEw6vM6otog3D8TLT+t6c2Q5Y5I1Ecrm8MS33NeMsqXU3vhEeBK0HMTEJ6UQt2pIzFWp8V5kwW6Ow09w4la5ce9toTgyN6Jx6qJjktQsnVk6zw+NgF2EV+uFIE2zIPwlpD65Ua8p40AjWZ3jCIw0lxIm4LQIvsI2BRwO1oKqBBIh0r9OYc13XNydMKdIgR6bqr5WjfiNmHYFEIDs1AqfBhZ7lj30j6YhJRpcb6bUdgUlc//cSWn3PJUi+MCeOQ3Z5OTnsIXyzbx4mdLWLOjNEEr8QReoAKLe8Dm3pbId4KVVdu4YtHTqMcAro4FSqBj5lqPPo7gu/o+7FiXh3ayTsZbq1CCZnjXsDg+eWlUEdIrYo63RdQufC346ZXl3H+9i2BDs1FSNW0SAT2qjsS20Yf7yCJCBbmUDBYxi3Fkjg3tUifaVxk4CyuwF9ei9Uol3C8TEOjzM7AdURVZRATYBK7/lKNuM3vUjj1VhPo29tziWFvqwCh2NddvjQH1Z4wk/f31CG8Qzzdb4vuzFVD7x7rBpATZIBCpZvv6AvNhIkZ5EWmGuQ+Ijrkwyt5sgzRA1rvwHzkQZ1GJ2ZNv5Z8PHDEAvXcazrXFKEGd4JAcgiN7tdxMAxJ8mdr2ae81qoJ32gjSPtsQmfCV6Lke6qcdgpHiAAkipKFWNpgjqIR2dgPtXGfNjmLOOHIUy564nrCus6qwGF03MLZXMucf7/Po1j3s7pWCLz+1zbYUASlOBylOO+dNOYyLTzkCuxrr7pu3Zhu/fezdFsd+PuVQbjp/Wufubx9giXwHqA01cO43D1KjRWbnOyDwEPmJ2mOHhhLBtr52tFV2cKv4x/XBs7gIEFz3n6tiG9Ir6OcMYRfJ7+AkJWxoyGBESm0L/Tl+Ri1b17qZ9WQvNJuK0CV6jgO1JNhkZWhAJoFD+2K47ajb65CnaeCUcSVHFAXIemUzwpCgGUibgp7roW76GKi147m8CIbZkE4F2xo/oqHxHiRTjGWcf3oxu529eX/FKEKajTW7e5n7zEqi8uU0jghiLTBS3NScfzhqhRdFBkGEAXtUWWmmRrbpyE1ulJwwIl0HAzOF8JxMOLUK6mzIUtOfK3JD4Aqir0gzk5MBeHTUw+shUwNdYBR6CIz2oLjqEy5GCvfPJNwokmEd56Zy7EXVGKlOgqN7o3hDOLZXYThUQiN6mSGFTfcb9UESv/02aafnHR6QSfXPJ+DcUo7whwgc1h/psDU9rCQqWm8VpaoBIztqcnc/b/J95Ijm/YDtqsoRw/vzr2ue5ouX5hLwmQ9yp03Bd/lRbbaT4nLy5X1XxRX2Rp74YD5Pf7Qw5vjrc1azvbiGx687p5N30b1YIp8ktQ1L+Hzr7ZySnsr/qoYBcXyz7RGn/LHpe7iu70oGuHxUj3Xx/HeH83rdMFhcxC9uGInTFW8hzCDy7AEW1uUyOb0sKTtCUuG/JaO4q2AxbjVqsk/ABTeVsXjaEFatysDItmGUu0i/awsYBg3j++I/YkBTXLqe5Yb5EuXEaoSruTer73Ai13oQ1Rr1p6SQsmwX9uI6M0VBuQ/XmmICh/VDpjiwrfTFfUCs+cqJLZTLzf/exiljthE2FIKajRs+nMrKdf1p6WOJFvrG/5v94HpeGjqpcRYHmVEz8qtskAKjqU7kXlQJxU6MTc1CJssd5uKvOltzW14b+vwMxCgvcpvHTD2sGvgP7dvuPrAipJHx9ioUXwihGUjAtc4cAQhdIgW415TgO3awGSoK4Avh3F6FWu7FVu4lOCa/OYw0GSJzA21FAEmPg8D4fs2hm63LClBrWok87B+hlxJVEeRmpLY4vHXldj5/YQ5Bf/N8S6OLrC1uPPfENgU+EArHFfhGFmzcmYTR+wcruiYJjMqLSa29gLNzC+nt9OPsQA86luYfw1BXDXcPWsgAl5mMKssT4OqTFnP5ySuwOyUZufE/HiGcrNnZi8npZlRKovVshoSgoVAZdnJD4bF8V9+feXV9aIhKg9u4CHONvRfaBA9GgRM5GgyXDcOh4p84oOXCI1WBkIKxuvnHpRe6kCvSIKQgU51o/TOpO30UwQLT3yx0A+fGMpCSwOTBcQTeFGm3x+DWJ3bgSTOw2wxSHBpZKQEeOeszPKmx7hWHqpPiSBx9ZDYdz9ncuGGFaFlOmhPExvJU8EXlxy91QL0tti1dQa5JB5/adBvOb6raTfHrWl2M4g02iY/AfMY0pnQwXxt45hUighqENXDbCY7uTcOJQ6n72XhsZV4838VmXhT+kLnjUhxEsP1UvID5Gcd7GNjU5FbrtkbKdt+TpNoI681tBcO8fPmZMcUWf7ICLRwnc1wbqZdH9M/lzMlj2rz8wvVF7ZoYDCf5/u5jLJFvB8P3PIQXmnseAC+WjSQou2YAJKBFrxrA7dC4+JR12B0GE884LW69gL+IcQOKTD+7SNyJunDDNH65cRoz1s5gsdfsEf7fjqP4564JlIVcTTvFuVWDn+dtxqVogER4JN7LBxDunRY/N6shoLR5hCHXeWJdFHaFhhMKMBq/YZGLhfLTCBw7JKqxZrfLST+pSXAvkpOHbzMXH7Wi/f5jggUDbdaMndRtd09xReLYUIprU3nCSMFGHIWVsTl64lmpCOy7a0xxVaI+bEXgO3EotqJqM7dNFJ65W+N/ZmE9vsg3Cl9rAYz3QYT1phDVdstGtadUNZjRU3uJe+F2hDdE9jMLGPX1dgrGDuTVv7/NBUOu4ReDZ/LCHbOwO22ocVZDuxbvSNjuy3+6sN1rZ6S2vxpd7egCRkCXBl+WrOaW5a/wl1WzWFaVXMrkjmC5a9rD93zTS79ho0HvwH6g7RAw4g8PVWFw+q9TGTR2ctzzjtDzSeU+rAi7qTdaRidIBJ9WD2RSagkzcpqHmNf0XcuRaWW8X1lAg26j9CcpbCnIg/UJlvq7IzHrOuZqy6gfuugdRDnUC26D+p8MxTG7BsfrNRDSwaHiG9Ob+5+aibG1kgd/dRc15eZ7mpalYY8TMWRXDdJdoRbaa0NjVN8yVu7sS2JVNSsIYSBldHxr4//xoiokcfs+cZ8L0kxulqmhDG5AbncRGJ3fvlskma0NI/bLNnrO/iMGYKv0EfY0P3BDI3rhmbMF30nDTIMVAbqBfVcN4YI4oZCNOza1524J66h1AbQ+rVL1tlUv0q6IszI5+ny7SIlSVg8OGzKyEvqut27miok3smfdnqaP5eU7/kfesF5xH98pa0oJTBgQk/fotT9dmJQ4jx/SN5LMLPHDytbBUY4hDW5Y9hLLqrbh10MI4OvStVxYcBxXDe+6uHyrJ98uze4At6LhVrtuSJZv98U9btgUzr/7kcQV9eqk2p+evZ14AqggOS17V8zxiWnl3FmwmPuHfs+LI77k8elzyM3zIeK4p5QxPhRdIaPQ1nLXouwwysQ6hMcww0pdCqEZmQR/nYNr1+6mYh9vW83kGUcwaYazKUXCiu/SCAZiv5K6obBkW8RXrJsLiNJ2l7F6Z8RfnVCsJTPGrWfqqEJsio4iDBRhcNYha+LkyJHgbKO3KQAl+rwEh0Q9pQr1mFpAEO6TTmhwdmzETCuCh/RKLkGxIBKZFB8jxYGe2nLOJlSQDS4bmbNW4F5ahGvFLtI+3YCe6uy439yQCH8YpboBtawePc3VZs6gWPvN6+mpjmY/f2s0vaUbpjVSouypJf3j9QTG9AGHSta4AaxetLmFwDdStqWMM649FYfbjtq4GE5A9jlHtBD4UyYMY9kT1zNiYC+SQQjB0388L+H5WbddnFQ70XxfsblJ4MH8xgb0MC9t+5ZSf9ctQrNEvj0czU9URcDlvdfhEl0j9FsDGfhb9eb9usr84DSy3G1kRVQSL11vclkaMDN/NUOctUSLnkByz6gB2NQBces2IgSMcVdy1eRFOFWtRRvkhky//Io0atelk2r4mlajKof4YkJEcSmET07DXlvVJKRfG8sJGxq/uusBXNkS6YRV33tYNd9DQ7D5x9gQtPHV+sFsLM0h9b0NZL20mMwXFhNa78VAJX4vXpDj8fHmNa/z17Pn8o9zP+f725/i/d++SE6Kly8fgtE7VpGmNGBDM1fz5oZRDqsnoRvn8DrEIQ3mCMZuIPoFUadUIxyRlcJVdtOrk+Fq1/8c7pue8DISMOwqhl2h/tSRbT4wtEwXRlYKTXludAOlNkDDEQPMydzVxbiX7cZeXItrU5npq49nWyLxVwTSbcfISkHvl5nc5urx2nTYInMLUa7JsI5aWk/a+2vIeH8NrhW743+UhsReF6DuJ+OQHgeENI44fAiPXf10wku/99jHhAyJFlnFG+qVxhaP0uLeP1+2hav/9Wby9wOMG9yHxY/9npnTJzUd65uTzrInrmdY/9wOtQXwben6JoGPRhEKCyu3dLi9ROy1u0YIMQB4EeiN+TE9JaX8lxDir8AVQHmk6K1Syo/29nr7nPRbIPghSDPPyfl5W7ALg38Xj0/obkmWGt3JgzvHcWWf9WTZg1RrLtZpMzhp8B1tV7SPQwT+12YRpwIo8Oqob1hi/JlP9iwmz+ngouEzSXP1xwhPhcqzid7eyPxd2gAJ6iAcqT/h7GkTmXrCKE65+almV2+FE6PCabqppcHsP73K9AtPxzemH8KTYDNwDYwCJ6KPn5NTdrPMmUOxvwZnRioTnzmDL2cvRKwMcvsdI5hyZi2nnOdD1xXeXTGSr9YMwb2sCOeeOsLZKRgpdkLDPZiO8tiLqYrOGeM3U5Bn9obqA3Yu++9P2V6RZXqafjKCs6bN4ycTXqC4NhUtBA+9PYF5y0dGWmjlm3HrqANC5n2NiLPBSON2h9F+8zYw0l1Ilx3hb7laWQrQ+qQTGJ1PaGBWc685kR88LSqGN5K90fA4yHxtGUogHAkYMj8014YytF6phIbmdU+4feseQiOGBGFG7oiGEAQ0MwVGSEfP9SAUBaXSZ64LibfyVgjCvdNQqxow0p0g4IpfTuPbP78dP4QX0P1a02uAhskFcUcgizZ0PCJGVRSumHEcV8w4rsN1W5Nqd6EKBV22HOUoCDy2theBdYSu8MlrwB+llMuEEGnAUiHE55FzD0kp7++Ca+w3FCUFI28+eB+GwGcoShrnDLuGn42dxie7V/Ds1q/Z5a9EIDCQuBQ7QSMcdw/Q1tiEpHdAI6fvUoSq0gtB72SG1O6zof7/4p5qUV2kQ/bLHGkfyZF9Ww41FftIjNxvwfcAhFaCbQik3YJQ80GGEFGjBSPYgKKq6HHym5w8qhCP2+DOK+dz9zWDaRiYj36EuzllbNMFIXRcKjnVFfz5ojn8c+dE/n7vf9n80DIISZjkQRvmxLaigW8eTmHOwylog1JBCZG5awnCMAgOzsZRVI2sD+IorkPLq6LPLzLZWN+v2ecrJbqhsKiwH5+vHcJ/5kwyxd18Q0CAP+zgoS+OIy/Dz2EDi7n45XOo9KaApkbFoUe9jQXtZC1UQJbZ2xX3RvvMiUi9KVhHSJCqQDps1E89JH7++HjEu56qEO6fiWtzecuimoFrdQmhYXmxdboCIcyRQqIHkpRIjylcTY8DKak7ayy2HVUo3mD8eQxFYGR7MNJcqBU+bA4b1eEw9ccPIXX+toQT2NEt6bkJUiZLyWfz1vCjY82UBeGwhrfah9/rZ85r85jwo/GMnDQsufvvBDP6TeCNHd/HiLwQcGzeiAS1Ok6X55MXQrwH/Bs4FvB2ROQP1nzyuxoqmb1rKTWhBo7tNZLhqfmc8819hBL0NM2lJZLf9V3Jz/oOxpH7eIevaXhfAu9drY66Ie8b0DeDkoNiG2yWNQw+2LUEvxHmpwMm4VA7vpvReXe9yJY9lS2O2W0qV5+4mEuONaOPVq3M4P9mjaH0x/ngiHIzBAyU4hBGHwe3sICzjtrDs1tHMusUFyIYtXKUxI/FwJBsnEU1LWKepSoI9U3He8IwaJx8bExfq+gYEgyZeLQ1qk8ZRw3ZySsLxhPWW2+B1Sz2ymF1iIGhhBouDdC/yAJ/En0mzSD9gzXYy7xIAcFheSi+IOF+GQRH55upkTu74Clit1IfJHPWiph5By3TbW4K3qp8yx1h9lHMe3vRPPHs0HSUknqMSLK6rBcXoWix+tX6e1R10RFND5gWROZ3ThtVQP37q1g/b2OzOZH/bQ6V13Y9SWZu5zcvaYvZu5fyz7XvYYtkMlSE4KEjfsm4rEEdamefbRoihCgAvgHGAn8ALgXqgCWYvf2YGUMhxJXAlQADBw48YseOxKFOBxtPbvyUZ7fNBSS2SAyeW9EY7Krjsvz1TEqrwJ77P4T90E61b2i7of4BMMrAOR1wgO8fpmtJZEL6ncwqTeXBDbNb1Eu3uXls4uUckpGHiCSgrwx6+a5sPbmKg8Jv3mXhWxvZucNF+ugx3HHPJWjArx+chaYZBMIaKU47+dlpPHrVUHoZlzf9HstCLm7edjSFgUyCumqGZTO9uQAAIABJREFU8wkBYcngikpemT6Xl//Tm9cfzEdvAOEE51AHdfUeHEVVxJN53eMARaDWx0lFoAjslw1Ge7EQwxAYqU68Uw9Bz0uNKduazBQ/6e4gRZVxfsDSXLFLvoY6ua5FiuToIkKYK2X1BRlQlSDyqvE3FtJJ+2Ijjl21TafC/TKoOzXiJlIAKVALK9GH5XZ++zvdwLW6GM/C5t+SVAX+w/rhnzgwvn2y8f+IRNqUrhH8rnxoaDoEwjh21+KZs7XpmxLduoxzzD82n4YjB7V02YR1XKv2kLJkJ8GCbJw7a+JuWAPgcNn5sOHVrrmHOHi1AMuqtuFQbByRPRi70nEHyz4ReSFEKjAXuEdK+bYQojdQgfm+3wX0kVJe3lYb3d2Tbwj7+HLZPQw05mEL2UnJuJCC8Zc27fZSHfLybdkGBqTkcHj24C65pi4NNtUVg1ZETsN1OIQXuyJxKwqk3YXiObtLrmPU3gf+lpNRUsL1hcexoL71JhXmZz7UWctwj4aq9uPD8iDjUsq50/M9DrtB0C/48KVc3ns2h/8n77zD7KrK/f9Zu506c6aXtEkvpIcQWugiLQqCFAsIWMArXkVBsYJeuepVsGDBqGC7olxEepOWhJKEBEhvk0wmM5lML2dO3W39/thnzsyZOTOZNBV+3+eZB7LrWvvs/a613vf7ft9QmeADj3yMZTPfy1Nrt9PY3sO8SdWcuWAKuqrSsP1MxkSacFyFt/dWIgWYRS6P7pvAzpYIatrl4qo6PrK4jh99ZzzP3ZtJkqL/owzPUpBtDon2/s/TNVR6z52BXVVI8Z/WZfV8cnqiCLo+sojbZj/J8tu8foqTy2mfl6EQDgvJSVMaiCb9bG3Kw7DoM06KRD2/HaEP3S3bNdzNYZQFvbivFYE9uEqLROlJInUVqWv4draitsVIHT8eN+xDiaUJrKlH7U0RXTbbU8yUGfqlINe/f4gzbpGyKP7DG54rSFNwgwY9l87zNPYHw3YIrdrjZShbDqnZVVjVEZSeJOaUUhhB7ndYSInW0otIWtiVBZ4LynFzFToPEXpdBwXP78yyuYa7yuCZvASSi8d7FcUyz9e3rYXQ63uzL+DBWvR/rb8+ZrP5o4FjbuSFEDrwBPCslPLuPPsnAk9IKUfU6zyWRv5zb9zHpaHfcXykjWAmASmZVNi5fTZlpy/nY6/9jJjTP1MMqj5+f8p/UBM6uj5MadeCGwV9NkIcfnDFTW+Ark8BXXhTwPyzkI6EwUXblo2QqSjRhcsC8wD/M3sNmibRDWjvDbJq23j279R47Ks6yz7cyoUfi1Iy/sOUTPoUxO6C1BOAS6d5Ik89toe1zwao/YeG7Wq488r51g+3cNK0/dkJqRBw3rj5+Zsq4IyvKay+yyKd9KobRS+chTUmAqpC+LntGHs7B2ui4RT46P7QQpZf83fufH8ZvVcupNMt6L/oMH32azb3XPUYezuKuev500hZAwzZYANaYqGe1I1UgW4NHJD1AeT+zO+nMEBXZwBSJgLhGVYhEF0JZNg3ZEaJ5Xjqm8PN3LMJS/RTEYfLSh1wTvC1vSi9KazxRaSne9W3kBKtKYrWFsMN+zwZ5DfqUWJmXiJq/OQa0nPHjDregBAovSkKn9jqZd8iEK5LclYVRkMXPVcsPKwVitKVoOihDZ4m0mFCagpuyOiXk1AzwXLLHdp34dU3QILaHqP3A3OxS0IUpBy+fNXZXHhhXnv6L8MxLf8nvGnwb4FtAw28EKJaStlXSPEDwOYjvdehImWb3LvzWdqjD3F6+ADTQz1ZAw8QCLjMnLWZ6x+6jVhlrjFPOGmufe0XvPieb3I06zoKbfSBHNduBWsN6DNRNK8soOumofOzYL+cPU5mAjf5mlkSMKkRUeplZJgPVWBJlTeccfx1a5wphVFqW4v59csnoKnedVMfU3jyha3c9N+vYqaXY+7/E4ZhAyYpC367v4Mnpy3AnqpQ8J8mE9e3sPfrrXztP2Zx/bdL6UjO5PPvedBra35VW6SEXk3nrsd2csfVE2iNhrCqI9nBKXFiDfr+HrBdhOvpu6AqxE/zKhdNKOpm4Vcm89juMMPzEz2mB7rEv7ibJ7Tx2BUKcnwa9mqZwSfPuZ06zjNlUGhBj84QeQOXfleHEOC4GLs70Bu6iJ/eX1lJFgWG/ga66rlGRnrH+vY5Dr7tLeiNPWgdcbo/fHx+g5kZFBInT+wfIFSvCHrhk1tR2+MIx0UKEG7/iip+/DhS88aApiJ6U4RW7kbpy6gdJk4gYmnU7iRuoQ837AcBBU9vQ4mmcp5kYPMBEKA3dGGNLxpG538YSInak8rNxzgESMCsKfaqXTV04/o0es+ahlVTDALUziThFbVo7V7eilVVQO97Z3qDAF7QWomnQVXoDSl84+GXKYwEWXrq8LUP/p1wNNg1pwJXA5uEEG9ntn0V+JAQYgHeM94L5JFTPDZImyZf++t9rCzbS0BxSMoxrOiu5EdCcFHJXr407q3su6ooklsnv8WN8XMZ/IHHnTSbuvcdchDkSOG6LnReDfYb/duUSvB9BJJDFkoHtQ+NygiFnQFpg/NGhF9OmYswbdyEilvkYnZkgpkadJx1HKazGn/AQbr9bJN7mhbwZM9EUhmphy7bT2LBWMo/3kz0t+3c8+QJBAt93DwKJdY1+2fwnVm1fOv3ddz4kQUI10VmUjncSICeyxfg39iE1hzFiQRILRiLUxLkM2evpjVZyMoDM3DzFuMGjztpozV2I69Q6A3Ck12eS07OSgICgUCZkgRNItt03K1h6JNgdgV0G5ls1mEeNIAj0WvbCa/aQ3paOQiBpjicPGUfq3ZNPPhDGAmaihv24dvXhasr6Pt7PIMJOQMMiuj3rUvQ9ndj15QQeHs/WlssRyOnD71nT8OaWtY/IBX6iS2bjdoe91YhcRMZHLDacVzCL9Vi7O1AqgrCcTHHFZFYNBa1O5lPGAIkhFbuoecDc72sX90r4O7lAojcV3TgS227+DcfOCzmpwQS88eQWjQWX10X2oEovcuOyxQN935IpyxEz/tmU/zAmyAheuFxOastaYCjq+hbm3GqCnGL/Nx1/3P//xh5KeUr5Lcg/xJOfGO8gyufvQurzHvpk1IDBGk0kPBERw2GcDi/pIGZgS4sUyHZIJlzoImdj4RxbQNzRjnuLBdldoKfbHuKOxd+iKqA9zFZtsMLb+1i9bZ9VBaFufjUOYwpLcR2HdZ21BK1kiwsnkhl4ND8d27XHZD+P7xpYTFeOGPgAS15DfzBICU4B/s8BF7WpgAUUIIuoqSHaatbuTy8lc5mlf97dhKPL63h8gv2ZH/tHkvjie6JQ7R80lLDuqQIeX8rSkEUOS8I+qlgvcrcs+OcfFo3ji14+ZFi9mwJIAE1DJeddyZfvnwdV36+AbUnxWAxYzfs8+qA9onjC4EqHH718hJ+s/IE0vbQ6Kih2ly5ZBMXnbINR8BjHZN4uHY69u4AosLyarTuCaBUmV7d176uVJuo5V04LxZDWkUkLdTuBLLQwAkFKA3HKQqm2NdRhOUM4LNrAhk2QEr0ph6mVHVy73VPoGsOV/z8Klp78wSED862zfujiVQuz17b14U9NpLry1dEVgPet6MtL+XQ8ms5Bj7bFyRatQ8nZnlGecD+wLoGz33mSITjrY6Nxh7U7uSQpCazppjE4vEeDbIjTvjFXcigjhMJoHYl0PZ14ZSHkQEdqQgvmSvjSkIVBNftw9jfw+FAAMGNTfgauui5eC5KZwz/xgMYjd6MPjWvOlNcRpCaXYWSHL7Smt4Wo2DVHtywwYHzZh1We/4VOOoUyiPB4frkf7r9af60d5X3j5xl5XBfj0tAcSjXU/x3+SvctHQqbkLx2BSZwFDsrCmYk8vwbW4gFIjx03tuY9KkCVz/w7+yr62bZNpCV1VUVXDL9Uv5VcdTmI6NRGJLlytrTuam6efndfVI6SKTT0FiOdidQOsh93k0aDYDfGPviWxKlA7zHAa2aeiKIJA2eWrO4/iDEinh7i+O59ovHaC0yittuD0e4Ybas/IKtoWEibpsH13fOQ51nskXZl7AFYFPIKV3LZlJvjTTCrEeldrOCG8//lEWn/gb7vjqcdgNaZyIHxnQMccVkZ5dhdRVj82iiEH9yf87K8Ll19c+wozqdvx6Jg5jq7wRq+CWDafjvlzsnedzUM/tHMKgkQ7I2gDu5kD2FiVdrdx5zQrmLYxiu1591bufPYXH3u6f1YmESckf12GWB3ngxQ1UFCdQFHhywzS+++QZuf5/y8G3tZn0cVXeu6cqDOcawXIoeGEnRn0XUhV0X7kQt8CfZceoB3pwKgqGJv5IibGtheD6BtREvxGTQOzUiZizq/PfD2+Q/Mp5L/HtR89E6l67teYohY9tHhIfyYfU1DLPZTUoDlH41Fb05t5hFYSc0iCuX0dri+UWGD9MSMApCqAkTYTpZNvuagrpmZUkTp2EUduG2pn0lFcHu8Fcl+AbDQTe3u9lJQd1/rz5x1RNHJ0swrHGSD75d7yswb07n+s38JA7ixnWsCkkXZ196TDXPnAqbsLzuwlAuBLhuIRf3g22S3reOGLBMJ8/93Z++8ir7G3pIpn2PhTLcUiZFt+ve5guM07cSZNwTEzX5qF9q3m1bUfeu8vuWyF6C9jbOVYG3nIFn9h5NlsSJRyOgQdIKhrXXTCbzlYNRYGbf9jAMw8Uk0wo2K5gnL93mMIlEn/aIjW7CiIKCNjR+ktAeoQVBVQNNB2CYZeKsRaLZndywWXLeXj/bOxGr2CJ1pNCb+4l+GYjRX99C//b+9GEnac/+ft38tQGplZ2ZA08QEBzWBxsY1ZDqv/sAjtv4FSoQKnlqUBmiop/5+a1zF/QjU93CPkswn6LWy94leNr9g840XsG0+alKAhbWffzRfN3cdtFK6kojJHhLOLL0PgKH93EmPZ9+Ha0Ely1G+VAtN/P77pgORh72tHru5CaQuq4Sty+0ngZZUqnahi5BFd6wcaElTPJTh5X6Rn4EbJ0gz6L98zfy7JFuwDwbW+h8MmtQ2br/cjNe8ibbaqr3oqMXIbVwMendSQw9vcMMfAyz/GjgQDPjZR2cgYnxXbxb2tG9KbwbWtBP9CTX2fHkWhNPdlrKQmLB77798NoyT8f73gj//u6lUdwtkBfGSOfFI0UAkNpQb2wA+dTAbqXj+cPxnOknUFc7SIbmUcCN+lYPNywduh1ra2QfpqDa9cePtZEK3nflotot/1eVaXDhQs9DSr33j4G8Iyzbkiu+87xvNZbhV+6nBusH6LlYwiX6MOSxCk1KBVe4O6copFTyP2KS83UBN3t2pCvWLgSJWUTWtdAQdDylvEHka4VwmXhhCZCvty2tccCfP/J06itr6DPIsqEmrekoHSBWP8qpbKwl3kTWjCM3GN9us3Vp2TCUbaLb1c7INB9ckjOz7L5O3nic3/ki3MfJRjfTnBXA+bEEqKXzady+x5Cr+zxqnCVDyhXJ0Ft7cW/tQVrXITes6eROHkSQyy6qgyr9uivbc8e3dek5JKaQcZ9UL80iw8u3kzAsLli8SZIWgRfq8tOiPJD9Ot86mp+yiZgl4QGnDF6HAkFYvD6rw9SEfhq29GbomjNvZ688yCdHaOhG601lnPe41v3YFrDu3f+XfCOlxoenBJ8qHCrdJIfLQEBxqoY6t4Mm0CRiHEmQutbWgukH5T3dOI+N4CJo8phpxZxO09BC3MtA/VijjZ2JSN8ue7kbCD0YJASZKMO1Va/Pxog5WL8I4qbhjXPRbKbTVOhYWk1X6qrQd+TJPSVfSz9Qz0bQ9VEHYOwa9L1agHpcCViSgIRdAkImwojj+bLYCgwtbSTPQyTkauD8+daSjoS4EqcogDx06d4BcMHf74S2nrDpEwVv+E971ha5+rlH6QzHsAZqDuU0JAdOpRauS4bF9zdgew/S8NJLEfNWRmAt7KvjMTAtFF70wTWewNa3UsuchATZ83zBXzr+ok4tsCPlxuoGEmPeigkqZkVHrVxoG6NKnDGRIh+YN7Bn6HESxrqC7wqgtCrdYi0jVVTjEjbaM29OKqAQQbYr9u4UmCoDqajcsaMvXzi9PUABAKOZ/xGOY2WgLAdb1acZ+BR4gcp9jICjh7XLXM9yyW4dl/2ugXP7SA9rZz0DM8V49/eilHblntfAd3TSvn8V3/P975yJUIICooPnoD3r8A73sgfKdLXlWVfXPMDxfge6sL/505QwVkYyDlWCMAPBCxIesZfdOsIZei771d03lvd/1E+VL+aHdEmrq62GXfsusOfW6eRHpZhMgBSoj/Xg+8PnYguh9R1ZVjLIl5HNNBX9OL/tad/oqhe71wXXqmuwR3rGWFrcgDrVxMoeb2YJXsDrK9J0+BXwQfKST0oZRYgqTTi1Piio2r/Fafv4jmGqdJjCLSOeHaM1LqSFD65le5L5+EWe7+VIiSuFEgEz+yYwn+cvYa+E57cMJ3elC/XwGfgri1EndmNnOR4ViThqWwOnMnvaStGU4ZOKkxTsP7VCAUv7EJv6Mq6A+yk4Ns/XcS3v/AGmuripCS3f2xSZnYvskZDb4uj7Wmn5kyVTU0lo5PztV3U3hRuQPekEDJQ22IUPrkVa4JHU9QbukhPLaPro4s9lUoNSDkUP7sZ0ZtGFvTnaqQtjd9e93dipsGU8k4qIx6lUEqoCkc55327WLvq4CY264KRENjYRHL+2CE++eD6f49yefliAkKCf2ebVwBmmHPSE0vQOpOskZ1cVubleBoBg+8+8zXmnfbvxbp5xxv5MiNMuxk7+IHDYWCARRWkLy9Gey1O6oYy0PMbS/XsbrQXqtBQ8Bs6100+iV82PIvtOji4BFSDKeFK3jfueLZ0N3D96nszgmXwjwMWz8wRGHncA0eCPrdAbW8kSzscFq7Ef1czxkux7AsevL8d94EO3HINtdNBxD1jphsuZ17SjZTw2p4yNszKTYu3ig2u/cZllIVmk3JM6qItfHLNcsyMYVWQ/Gray8M9yhzYluBLl033Bs1BfHrpE5CSiMGLIMclsLEpw0fHo1CWmKiLeon5Xf6zbil31qyhUDV5c++Y3KDnQKTBt7wbTIvEmZPwUlyF5xpyXdBUUnGFe59ewKfPXY8/6D1w2xYkehUe+VYAo82bmUtD4JZrKC0OKw/M4Mr7anj/ou3s+V06a+AHI/zKHlaoUwgXpOnMV3RkgFvFt6mJ4BteOTrhSsyJJcTOmAIIQq/XoVgOvt2ezpAUXsARTQFN8ZyEAZWuc2cTfL2O+Lkz+mmTCO59+QTuuvIZfLqdc2t/QPL1ZRu59cWZ7HjCYGAoJq+hzPw3sL4RkbJILJno1bC1HQJr92Xbl/0ZI37ip07Cqo4gbAffthaC6xqOKPlpNDjUVUHfz2c0dmM0diODRrb/ZtLki2fczt97/kC4IDDyhf6JeMcb+TvmXsFN6+87ehfUBL03zkBMSSPy+M2FAKlCyRkmt025lJOOq0FXVU4ZP5VHGt+gMx1nacUMzq6cg6aofGLNr7IGHiDh6ny57iTunvzaUdeB2rg6wI59VYip6bxaK33wLW/NMfB9UFISccDKxCgkuiGpqklzzmWdfO8zE3js6kUQGGBshMMZxWmKAjP55oa/8uyBjUgkRWqSu8e/wSyjB0d7H4WhcyE9MqNWSvjRLePoau43wtInkKpAWBLrhBD6m3FI5H70QoLalQAJwTV1JN4zDvXknqzraUuqlIu3XsCEZIr2ugpAgiMJvL0f/5ZmhOVgjYkQP3EC/u2tSCFInKaC1k9BxHTR2uPoDV28uDXEiZMqqa5OoiqS12on8MDjY0i47QjhIMMK6StLMC8shKdV1N0xmprKuLf5ZApf3YTG0OcuAJF2MDf0eAlKF5Yhh4jyew/J2NNBaO2+HKE2Y28XIbGH1Jwq9JbcCY+Q3v50H4Mm0yfXp2FXFOTy/qVk7dYqPv37Zfzm44+iDFqfGn7JFTe2cseWKaiNplc3IDGY6Dq0b4EtLfi3tCD9nq78YFaOG9Tp+cA8pO6VOZSaQmpuNU5RgMLn8pMX/pUQ0nPxAMie1JD+f/P93+Xul779z2/YMHjHG/kl5VNR8GR+jwakEFDk4vYqHl88zxssBLT7Ozltbn+t0onhCj4/86Kc4zZ01eHIND+a9DqLwu1IAWuiFRRpnj7lkanRD23T3BOTBFdrJCeZSEXmH0SiNr4nosN/mKoA20VRJZap0LArwC2Xetm2wd3NOF8sx6wwMITNjeO6+OD4uTxZ+w1WtNhINC4r3cUt4zYMuOBDWDHQg6dhm6sQEjY3VrJ693jCfpPz5tRSGk4Q7VJZ+Wi/718WKqS/Pwa3w8WZ4gMH9OuGVtKSisAuL0CJpfFvaSX8HodOJTdHQaiCfYEAjtBBQvilXRh7u7KCVPq+LiIHophjI/jquwit2E38jKn9Il26ijAdfG/up/v4cdz84IU4QvNYN0jUizoRHywES3pfVObBKwvTyMYQfSG/1PRywq1DV50SSM+sJLnEWyXp21sxM9ztLFwXY1e7518fFHQWjouvroNEHvExCUhdIfh6Hb7trQjbxRobIb6khvTsqqH+cr+GVBRSlk5YzS1ooShQXZwk/u0JKDETpT5N8AfNMIrYowBEKn+xneTsqn6JgT5oKtb4IpxCH2p0dP774QjTh5WGMMx5o+F1bVqx7TDuduzwjjfyACvPvp3zV3yPmJM66LEHE8UTCogJB3+pJLC7t4UpBZXDHtPQu53X5j+afRGEgNMjzdn/P9pISI358xt5dcVk1KXdSP8gQy8lal06kx6evwHSEJAWuI5A1VWUDP+vekoll37mQhZ+8HiEG6Mg8VVU+y2Ir+S8sOCCubArUcDMYHRI3zQNejv3sb3wAT7/m6exmv1IW0FXHX7x4hK+dMkK1v3EJTp/IuaEYpSkhW/LAcQEHbum/xW1zgijr4pl5YklIFWPThjKsD6SLyThnDyJaI5ABG2CT9Vj1HXmuAEEgOXg+rxh11/bjpCS+JIajIYupBCY44rouXIh4RW1BNY3gvAUJOOnTwZ/ZlanCk/bRgARG3eM7mmZZ4yXObsaubrek2boe94AqkLipAmge301p1dQ+OhGYmdMBSFwiwKgCdSO+BADn/OcuxJDDZOmoMTSGPu6solQRmM3hd2dfOhek8d3zmVHc4ZIkPnh9rYVo6lDyQGWCW/viuC0BZDTwR2nI3+lIjqG0hwP5fW2y8OZAXMQHIlTHMwx8l6OhITB7rwRrn+4n1o+/v7AbY5fA0WgJK0hq5M/fuchrv76Bw/zzkcX73gKJYBhGLx47jdZe/5/s/q87zAxMHIprqOV//Vi86YR959vfKEvMTNr+EZROGhEpNNwoF7P2wcFSe8YF1Fq4rxY4mVzZqjWSE+r+q4T1wz70ksB9Lr4zirj5uU3cNNPP853n/4aT8T/xEkPL+NbE17ikpU/5GOv/5iHmroBB02AoUg0IZkVyh9cFQJCoXqefrWF9IEArq0iEZiORtrW+a+/n81LY08jOX8sTnkYa0IxsffMwLc2jdqkYb9UhP10KbGTp5O4qhq3SEXqCtaECNEPTSe8ag9GvecPFzGJzEdeUiWyV8O3sz2vn1cAajTtDRyagjmxlKK/bcA1NMwZFVDgo/DZ7eitnrtFSND39xB5eBP0SNxWHeeZUpzXIjivRHD+UQL1Q+WRu649Aau6IMv3NsdF6PzIoqyB72uMNbYYtzSMWxLyptCuQOtM5OWVA+BIgq/Web8jHu1fKpCcVuadNzDTVYJrgvVmN7+57hHOn7Mz51Jx0+D+VYtImP1tsh1IOj7+/PuZsNWApIp0BMn/rPTcakr20ocMrSORnxKrCE+zZtC2nkvm4frUnHsNR488mui7vutTsQv9nqZNygZVwR0ULP/THQ9yafl1PHzPk8e4VQfHu2ImPxCKUPjDqTdx+vN3MHjslRLcbQGUSUmk/8iMrYoyonCZlCkUnKP25kkJPR0Kv71zDB0tOrfftxefv/81dyR02H62pkpQp8a8bybD5+5rpovkWf8k5p3cxcbXc4W8+tgQyi+m8ourv0hNyBsoTdfm42vuZUtPf+HvbsfP8pbZPNY5ifunv0CBlhuky4ft8WKeXrcNnHw8boEpjNx6plUOnf4KeNOfPUe2GqRCNVj3FiIKHbBcfI+3oR+IApLJ81MUnGnwqiOxhfAKiQPSBrYCCYYV7JSAUxLELdcx318AsySJc8cgd2kUPLsdrbkXYeUKRAgJpGxCtzQSO2smhAe0PymxN5UQ2lCLffb0/r6pKr0XHIdvewtqNOUlBWm5zBMAt8CH2hYjsKEJJZrCGlPIcRPaqG0y6OOi57QF0GIDBhQJToHhGfc8UgZmWqF2U4CAYXPbspW8sG1KvzwD8NtVx1PXFmGWtg9fLIFTGuLB2sV0yDS+jS2klGrERAtzjIHzuRDGY53oDVGUuHXIr7xR30FqbnXuMtt20JujnkzCAEgg8sgmr8j4Id7ncJBvVWJVFWI0dPdPFjJxDdenoqQdb5B1Jb0dMX75ud+x/JY/8kz6L/+E1ubHu87IA/g1g9vHfJjvN/6BlJJ5caXAbTAQpTYchfKJmqJwTtUIxT7k0Sn2Df0rj0DYJdqlsv7lQh74SQXX3NqSlSBvNYPcvPs0QCAKJNrieB7XlODp7om89Oe3+PltY3jhoRJcx7vu2C/42HLKdH6y+FoOJLu4a+vjRDRBS7KOLdGhTldbqjSaYc7dfDFBYbGstJ7rKrcQ0ewhxJCEo/K7thlYfhOPgzoILpmi3JlWVqYRx0dxnysdNCgIbwm/sgj1pG6Ez8H3SBeTZyf51u/qKCyxMfwSKddxx+YTeS45HmyBuzuA3GmgtsVwDQ0lZec1EP62dpL3jkcJKDiAjAkK/3c7IjX8/FQAWlOKyIObiH5grid81bdHUQldXM2y4zYRNf386CgxAAAgAElEQVS8vH0SyZTmaZmv3uuxXjKXVroSnhJiawwQ2OV+Qq95yotCgtYR50BYRTMktjk6GqPaayJ9Q+r0AKD7XCbPzhhQCdMr29nSNMD1aDq8uHkyL7qTQFEwnmvHt30fhk9Db+xGxEycHWHs0iBWWRnW8YUU792Q914jITW5lPiZA5RZMxINxs42wq/vzTlW4rGJ+ozr4fraRwupKvSeMQWtI05gQxMCj6lk7O8ZshoULpDJzh3cJsdy+M9TvspPX/vvY9ja4fGuNPIAEwvLuLy7mfedvIkmM8TtvzuH7hNs8LvZGd7hwqdofGLK2UwKD69bIZQwMVMjqNtH7H/vO9/nh6/8sp4PLyzg0fvKWXBqjAVL4yQclQ9sO5+s9y2uQMgddqWx1yrglh818oW7GrHSAtdQuHv/AtZ3Wty49tf9GYsy9/55WgZAQhr8rX0KD7VP4cqyndwwZhsaLpoiSTgq62MVrIqORalJ47b6wBl0QdPB2N2OOcsr+qHMj4GpMETSt++ejsB5tYg5u9dw8mXNXHNLC/7ggPiDkHx77mpaf1/B+vqxAGj7Oyl8dvuwflwBJD9YgqVp2X75/rcT0sMb+JynYDkEV++l94J+jrSqunz09E1cdvxWbFfhyxeu4rN/uJDG/93vGe6uJL7adszxRUQe3eSl3GdaprXmKjkKV5KKq4yfa1G30Rjik+5DUZnFZTe28dj9ZbTuN9Da8k02PObUsms8GqOqSHpTmaIefeJvishZYZiTSxGWS/iVPUggsK0FtrUAHv3RzCRaHcqr7moK8bOm5a7gAGzHM6R5XDgDDTyactDM50OFVAW4ErfAT/ykGqxJpVgTS1CSFv6dbbgBHaV3mNjfCK/KttW7jmo7DwXvWiN/XE0lf3u+mPH+OBMCca64cBO/7p55xFGID44/iQ9NPJXxodIRjzsQb+aq9RfyzJInMAYl0ByRm0iFJedEeeWpCFXTLf7ePom/t0+ir2PSBmdTAepJnn9cxaXCSJJ2VJZGmnhvUT1TAp4Gh6KALyBJuxJXSm4d+ya7UhEe75iEC4RViz7XQNzN8MaHgZO5/wPtM1kfr2RZyV5CisVLPeN4NVqNRCAqTBiXgn0+j5GRGUUKntuB3tJLXEJ6dqUXyHQY2cFrS4Izirjha2/nLwcqBcctreetmiCkBL4tB/K6OAZusxcGQe8/QtuRGpUIV9+1tObenG2aIjlxciM+3cGXyRu4+yPPcukjp2O87RnI0Mrd+EoCiEGFK/I9accR1G0wPKE2y8nzfCSOA++/to1l13Rw62VTqN3UX5BdKN4s+bgT4nz2u/sprbSxHUFjZyE9D+xHn+4iHBersgBZMGjFpanYpaG8s2e1J0Vg4/BSwBI8jvyA2a9UBNH3zR5a8B1AV0lPLcO3J5dLP/BIuyJMct4YCl6qzfhh5ZBjZJ7zRoIEOq9ZAsZQrZ3kovH4d7ahdsQxxxdj1OcWsJECXL+OOoKK5b8K71ojL4TgE++dmM2q1gst1LibNUaHiqnhSr6z4Comh4dn0wzEvav+m6Qa5IxNF3NT9WYuLq0jpA51ZRwqFAUCIYezro9yY9s5dFp+TNRscNXdFEa2+iCqcOHE3Xx+7EZ04eJXMkvJAffv+zYcCV+f8GZ2+ycrNnHJ9veRdDWcwyB67kwWc/f+YgYvqIUAbUEMfeMBxFYFYdoYdZ3Zsn7BdQ2kj/Oer9BAjE8h9/nzz+g1lf3RyNDteH26te5U1sfLUYq9a6e/UIacoRP4ba6Ec45h7bRhXL+kglOlo7SO3u2Wo9OiulRP7GRKRa67RFcdZi5KsHsDWSOhd45C8qGvjRKE6WQDt7lPRpCMqXz745M4+bwon7y9iS9/cGr2OOkKrri9m49e34hpKyTSGu2xIA/+shxtb5TCvd7EoOO6E4fcV2/opuC57fnbxPDjsQTip9SgtSXw7+rPIE3NqMApCeaf8UiZpbcO55JxIwGs8UV0X7UQY1cbSsJC7UqgN3t9EI7Mror6W3kQCIauKvrul9HSV0wHN2TgBnSE6aDYLlJTPE19e3i5kkhZwbD7jjXetUYeoHrsh3Fbf4kQMDXQg09xSLiHZuTPqpjN9xd95JDvXWumwfC0LJY3z+GD5XuO2MCD98rOOSnOa8dPpa0rkB20hMjErSakkPsCfNTZyyfGv4U/Txp+H4Tw5v8BkZsP8FzPRBQk1hG/Hvk77Hu+HbV9qPEUSQsciUwIREiizIvh2AL2+4Zey3KYO6YZV+bnLn+8aistDcdTl8oMBH4Fc1kE35PdKM399x5oRHwPdZGY7ge/90zTV5Wg7WjKUjbBG2/yze6lgOR8T8gN1UVZEKNlnEurGcjV7ZEQDveglyjYXTKTOToMnXXQHikgNbea1JxqpOH5xoNr6nMYPLYlWL+ikM1rQ/gCElVzsW0le60Hv1XEUz8rYNpZku4OlcWzW0jsSuMFqry7qV1xnPKCft66lIRW7R6RvpmvB32Pyb+lZcgokJ5RkZ82CeC4+LaPrM6qNfd49NKwj9TCfqEQEUsTXFuPf1f7CGcPAwlaay92VeHQ+7X352gEtjRjji/CLgmiJLxSgnpTD4o1/PNZvvGHh96eo4R3BYVyOAi1EqF5OignFjRTrifRhlF/VHBRBu3zqzqfnHbOId/X7fkBC6s70DJL9MJBSSUHQz56ZB8VMhWHcy7tZkXPmCGrEqGAKLZBlVxz8tsjGvjsOXkonZsTpXk14scZMXzC5vCIcv1QovlnPDKog6og3w57szkFtMW9UGWSk0fvuGi2zY0f2URTNExnt5bzzISA2cFOfj3tJUq0Af5TCfb8fveFNAC/8Gq3Avq6BME/tmXYKBJnQZDEzZW4xSpSF0hDIANDzZkE7NJQRhNeopzQizIuja64bE6U5BwrbIfa37moCQddl0ybnwC8coaDn2rfDLlve/z0KSQWT8At8CN9GuakEnounY8b0AedBemkSrRL9QZJco1wrEPlrYc06l6CxlofG1/PnWWGVu3xpBzcTFlJ00aJmThhH7EzptD14UV0f2Au6Ukjuyz7aI1qTwo1evAcFsDL6t3d7pV6ZLjhzwsq+7a3etzOPrjesr2PTpvbikG3Gaa9wVf25CpQujIbbxkIo6Gb4IYm/Lva8dV1oqSHn8X/tf0+SqpKht1/rPGuNvIAovDLgB9VwPVVW1hS0Jwx5gN/ZklAcfhE5WYK0ilIu4wVZdy75JNMLag6pPu5rgvJ33JVRS16xsh22n7Sh7CCEP0TqJy/H35+DIGM0J06jLNYAH5dJeQ7tIElpw91JvogpcyzIw3MCHRiyUyptiOAuSwy5COTmkLiBC9jU3b40LsFhue4R13cg5iRAL8Ntk2p2cL3rn+KpxumctmPrkL3iyEDlSJAEy7vL63r36gJjy8vQAYE6YuL6f1VDdbSMNIn0AKS87S9XBnbnZ0M2KcX0PvHSSR+N4HkN6sQCTnUQKiC2HtneI9lTBql0nv2jhSEhYUrIW0ppJKC73+mhkRUI51UsdIK9dsDTLrMxRmrDftUBeAEDdJTy3OFvhQFqQmSc/okCwa1LCPUNhyEAm+8EMFM9/+mTqGf3vNneRr0XUmUnhRacy9uQKfnsnmkp5fjFvhxKgqInTWVxIKxw15/YPsHw7ejNdeY9h2bMAm/vHtEF1AfQq/X4d/agkjbHuWyvovIwxuPqMiI3pGg8JltaE09iLiJ3tBF5LHN6HkylUeDuafNoqTkX+eqgXe5uwZA+E5Chj8FsXuZHezlzn2VTPV3UWmkWN1bhS0V5gQ7+M/qDXSukIjPBLn4ziv56hcvPbwC3m4j4DLGl+AXU1fyPw0L2Z4s5t6m2dw8bsMhCZP1uWCkhHRC4cZvNaNmvvELS/byt/apmLL/o1dxmUiMT1xzHYr4+aG3PYMbZm4n1etH06BINXklWsXrvdUkXY3Rz+IH5yj0m5vUx8tQ6k209V6tWDeokzhhPOb0ChASMTOGVQyQUfpUQZ2RhBme2yMBlFWm+epPlqBqgrAvf7DLr7hM83fnbJt5o8tbn56SrQAGkPxyNUngPUX7iIhCfrdzJm4b+ApNHC2zstqQInBPq2d8BJ7xFB6fPXbmVK9CExIl7GT6Cymp8oum2ZyTiNDbqLPqPySd+3NllC1TsC9chLNAoDb2DJs275QEveLbg33GmpqRWs7vvR7pDVYUidBEjiyBU+AjsKEJN6gTXN+Y9Y3HT5mY0ZYZcH9dJbloHIHNB0Z05eRrh397C9bEYo9zXt/lGX0BStQrGCM1BbvQn00Ay3tNCaHX9xJ6fe+I9x6I0Xjo9aYohU1bSM4fQ3BD06ivPRiaofKVP3/usM8/WnjXG3kAJXwTMnA54801zGx8k429KrUpydmRBi4s2Ysq4NHvFfP6w2Xc9cJXmb909FKhjnTpSjUTMf+Mar8JyvjsvlnBLu6f8SK2FPR5RfckC6k24vgUZ1Q++j53SiCc+xF9qmorm+Kl7E5FcKRAE5ISLcVPp62gVF8x6vbnQ01VkrurXkcCL3WP5fmecRkDD8N/Hv3GX0Ui0zCvuI096Qi9jkFAtXE7XKxmF3eSj8S3xiCaLLRNCdT1SYINbRhmmuTNAUR45AdjofLVbadgWwJXU4mmfBQFh0pRJB2VrYkSMoVuCXyzkZ1pF3441Ee1INRKXSrCy8mxUO6JaFmWwPhTO/6/9yDM3MEtsWisV5LQr/dfSwXKzAFsH8H2dCnbW0oBSbC4EX1/rttCSkFM0zGvjWA804O0+5/wQLOt9qY8et9gOK4n0HYYqyvHEdi2yLmfsb8HmcdVIpLWUGVMyOr6D/RZjwZCQsHT25E+1WMWDaRGAonF4zEnllD0l7eOKh/+UK7j23n4VdtKxxTz260/JlQYPPjBxxjH3MgLIc4HfoL3CfxGSvm9Y33PvO1QKyHwfu49+SLu3Pwwzx3YyAs9NaxtmMLEv1osnjid329cRsX4kSURBuKRhjd4fO8f+dXUZxCAJQVCrGdbvJigajEl4C3xtD7XivFeplbfg5RpzOYluHYSVR1ib0aFgOrw62kvsyFeSm0qwlgjzpKClryMtENFVoIBWBkdQ9LNJ8/rfXoKLi4KCg7fqVnNGUXNKMDvWqbz+5bjssVLkq6Or8RG3SXx/9cBrJNCkJbIJj+xOVP4zNUrKGEnPwydijUKRo9AeJWbENzz8ol87r2vEVLtbP9dCS6CFXVVGI934ftLB5UVJnfcX8fnZDkdToCBn/w0fw+Pd07Czsh3CgEYAvOqUvxPRGGAkZe6QBbqyMBAWqmEsjSKaZJP6llqAnNpAfrmob5pe5ofgio935uG/74ejD2dSFXBnFSCvrcd1XZQYinU7jhOcThXVMyVBDYdYLiZ/IiQ/fyTgZ7rfFcJbGhCWA6JUyfnbPdvPoCaMfCjbcHA+4lBvuw+N03grf2kp5XT/b7jKHp86yg7dHTQ1z4lefgJjadcvOTfwsDDMTbyQggV+DlwLtAIvCGEeExK+c/91QZAU1Run3c5t8+7vH/jFYd+nb/tW8ODu3/P3ZNfBTyjoGeM+ZxQFzFHxZGDaMDWGlxzPUL2srztMqLRTdw25dCzBD0IhJAsCHewINxx8MMPE37h4Gl85houFUmVEafLNnBdwfVFO1ha0Jrt78PtU4dUp0pLDf+JEG2chxK1vIBhjQJIIuMEFy1q46ebHKw8RT0G44vT1nGrfxnugh6eqK7g+S3LuLF6MxeV1ONXHDbFS1j+1nQ6v9FNYJcJSL7/4G6qxpvo210Gm6PtiaL81bQciT3Lj74ukd0kFIF9AygHYri7gxi6TfncdloCCurOFE5Vn/JkLuypIaTaAU4uJ954LkpyXBCnqZjEdUGSehVui4H/iUbUpJ3V0I88tpXY6VMwMwFPpTdNeOXurL6LUFxkNvYz1OTmc1WMxvcNIFyJf1sLyUXjM4MbGDtaCb7VOOzgkM/oj3oosh2K/m8DybnVJBaOJfjW/mOa3dqHge07kvu99/rTjkJrjg6O9Ux+CVArpdwDIIT4C3AxnpLIOxaxdBs15s3cP6MTnxgqRywEhFVnyHYpexCdVyOFn0+UJXhaTuC+5plcX7U9e97Bs0wBBBQ/hNXzI3p61lMaTh4TVUuA95Xu5dmuCaQGVZvyKQ6Lwy080TmJcj3JJVW7MQbUum238xdNSEvVE3QK52pLXDR/G5qAp+Y8QcLVeLh9Mr9unk3OpyY9vuQpBU3MK+yg4KJWeoWBEN4A8pOmBfykaUH/8QUSfiAxnuxh0Vv1FJfbqFrfs801Ny1WcMg2APwqmAJXzwQnNYX47VWIQg1RmEKZkcIQNmeW1PG3R8YgI8MvzRy7iM6rK1DbYxS8WIua8AK0vhd7SS2pQj0rwwpRQJvoaeQ79T4SJ0/EGluEsF0if9tA+OVaj5dt5mrpVE8wac34/MuqLZr3Gdn+jGTIR/3quKC1RLHGFoEQBNftyxU+GwGHkpgkwGM4ORahTHGUfxaO1mf02RO+zhd+fQMXfPw9R+mKh49jza4ZCwys89WY2faORm3Tp5kd7MSv5Nebh/zfuZc7aoOM4VNczitroMvxc8OuM9gUL6Hd8rG2t4KnO/v9+n1GX0qPIfbnH5ez6c1LUHxzWf7ybJ7cOO3od3AA5oQ6ubZyG7pwMpRQj9SnC4fnuydwXvE+fj5xBX4td2k7xsjvow0rVvYafX9fumAFvkyA06e4FGsmH63YyQ9qXkFKmQ0+q9LlhxNXccu4DVy27UJiij7y4CYEGArmBRHcBYHss5wR7B5yqDco5aHaCYieNpveZccRff9xdP9gBu683GzQlNT4a8d07JPCONN9+TmwLshmH/g0nDERej68kDM/nebnz+7gvk074RQvwCz6xghDYJ8QInrTTKwJxaCryICOG9QRjkQZZOABzv9wJ/e/vo1fPr+TUKGT0x8nZJCJFQ/tI0MHgbwUQykpeHYHRQ9toPhP61BjI0tyC8ApULDmBkA/dAM6eCLwTsPdn/zVv7oJwL9B4FUI8SngUwATJgwtevDvBilNZvo2D5EqOBwEVIcry3dx+bYL+FTt2d42xeLOiWtyjnNs2LfLx91fGM/ODSF8P9vPL1bczHUnPYtPO3JtnIPhyvJapga6ua3uVLI8bFfj+zWvMSfQxX2rFnH9aW9iaP00jc9Ub+L2+hMGJVRJYq7KDeeu4fVtNZSEknz67LXZrNCB/fApLkuLWlheuhJVgX2dRew6UMrSRa18ac/JJFyVUZsNQ7ClshJd3wzAVeW1vBqtxhrATHKHme8IQIxP40zQUCakUCPD0fOERwbqozgO0FqQNsi9fkj2F+eWqsqWijncNmc7K7rGoCBxB/cnoCAmWsiOUHZTekYlatdelDxslg2vhVn3kpcI5Q7SB3Iqwqj1ncNO6e2gjpaw+vs8fC8Hcd6Hd8BIAYnvjSX8+QbEMNn+I7lv8koXHRHyZSK8+3Gsjfx+YPyAf4/LbMtCSrkcWA6wePHiI8uy+WdAmiijFTQZBcKqhUAiEQQUi4Whdk4qaM7uFwJUDaprTI47Ic7ODSHMpIlfeY6gMTQwNDp3z+jRaRnc0zSP57om5CRfpaTKd7csoWtlJSlb5fITNuPTbDRVsuLRCPffWUigsQ5/qUrqo6VY50UAAZbAmWhy3ymPjOr+88Z7qfCzx7Zx/lxP5GlNb2Xe4OawEJCYHGTNykJOOjPK/FA7F5Xs5ZnOGlJS9QK4rkDR5FBeuQB1XiLvZUe+p4Coixs3kPuCyGZjyCG7WkpJ2yp+zcGv2yRkvgB3bnvSMysw6trRm6IImetBXv/y0EzN7FXM/EFECdhlQbT24amKI8EfdDHTAjePhLQzL4BbpsEI8cth76kM1eI/cggU1WXRGVHWvZhfEuNQ8P7PnEdzfRtrn3jz4Af/C3Gs3TVvANOEEJOEEAZwFfDYsbqZG38At/U03Ob5uO1X4Nq7s/ukdJDpV5GJvyGtw1eEE0qYqJOn8tBhwpWC84vrOSvSyDcmrOMHk1/Ny1TzByVX39KCqknmnBilpDL/1OhIi5IMxs5kMSvzZNeCwApDutLGcRU+ft+lvFU/hpceK+KuL0ygtdHwGAodDoF729Cf9mh5Uld4qWd0Hru+vvT9KZmYhSGGW0UNM/gKgazUuaPqDFKKihBwbcV2zo7sQ+704zxdhvN8CW5czfqYpZ3f63JI6LVx1xZ6bpp8HHZF8uK2ybyyejJ2vmQ5UyL3DnJZqAq9F8wiMuPQ5mdqZzL/i6EK/vDoeiZOH71+Tp+D5+xLu/j5szs565JuRJ6JjzPOAEPBmekf6g4a5h2VgFQETtg4JvNs1xGHbeAHurXGTa/mpp9+nO88ettRa9uxwjGdyUspbSHETcCzeBTK+6SUW47Fvdzub0JqgDC//Ta0X4hb+ihCiSA7PwJuFyBBukjf6YiiHyPEoT+CYPGdpHo+i4qLrkivZsAo3sgMXTtbIxqgVE9ze806Xtk1gXsfPIn/6ipkcnkXN52zhoU1B3LO13TJ7BPifPsPdcfcRdOHOaEObDnUAPmFzaUVtdy/0EAZl6JtdYRfvnQC1q93kk4OkltIS/x/6sC6wPu4goqVVznSlbA7FUETLhN9vXn7uP1NP+8tqufx3smYA6iWunA4PbKfqO3jjVgF5xY1cEV5LWHV4uXusfy5bTppV+WPLTNossK81D0Wc2cIuTPkSR/b4LxYgjs2hSixkTEF2aOhzkogSnKnogcrIekdIxHVOuqpvTivFWasWv9JmupgqA7fffJ0kqaBUZWA4+OeEREem0V7oRc7VgI5iwCJ4XP57XMbuHHJdDqa883+h0JNWjgFPpSEmTMWBook4yaZlFVb1O/MHyzPh1PO7+HLP/PCbV+6p4E1zxcS68n9ltT6NDiQvKmC8K2NSMtFWB4FFSnzzvClpoAi0EZZ1/XwcPCPZzg30twzjuOG/7mamSf0a+BPWTiR3W/tHXLsz9b/S9jiQyDk0aqFdxSwePFiuW7dukM+z3UT0Lrg4AcOgATStp/P/flKaltLOH3uZD57yVLKIqGDngtgxv/G/rbvkXRhd7KQC0oaDmroXQldtkGpbmK5gl3JCAWaxbbaSr796NmkrP4P1qdZ/OTDT7F4Un/GnWXCa89EWHpRTzbz9Z+BB9um8IumuaSlV7bPL2zG+WL8fOrLnLf5EgKKxfcnvs6SwlYuqpmLbeXhiQuIPjoVYUtKfn+AP9yxlpKKfmXM9b3lfKP+RJKud48yLcX3J73GlEB/ScGWRo1IiQN+wS17TmVTvBRFSFxXMNkf5Z5pK1GRPNVZw4Ul9QQydUotV9BiBbl6x7kouKRdFctUcf5RCvZBFrOKRD21O2vopQMo+Y181vinXUSnQ+i2RsxlEVIXleC+UAqugiJcDM0haFj0JHw4A+ICaA6iJgUIZFqgVfWgrLSwqcANeIHTiqJefKd10qYE0B/oxPdgF/IQ7KEETy1TesHbMZPS3P/qdl5+tIgffXEcqcTBXyxNd7ntF/s47SJvdea68LOvjOXZv5Tk/PYSSezHE3AnGoiYi/FkN+ruNM4EA+OxbpTDV94YsX+QN4Q+7J7hrpOP/nn3ym8xL0+y5MZXtnDrWd/GdVwi5QX8qf4X+P15CuQcIwgh1kspF+fd964w8snnoec/Dvm8vq5f85tL2dlcRUlBkIfvuJaQf6j/NP/5JrL3l9y3+3k+VLGLgDpyMLbPCDzUNpmfHZiHiovlKlj/KMNKDJ2Rzapu5Y+f+lvO+akEBEY3Dh01SAmbEqU81DaZbtvPmUWNXFhSjy5cLtl6IW1WgA+V7eRz4zbx8dNm0Lh76MstS1RS/1vDub69nNu4i0VL4xiZ8oXtlp/Lt50/IKsWQBJRTR6f/WQ2yL3jrQBT5yZRM4ftSkbYnSykijjKrhTzTkyQdBT0TM3ZgUi7Cvfsn8tDHVMBr/ats6IIekYxEy42UU/r8aiUO4KIiIUYl5kRD7CJ3i0l9Dj4f96BsboXVIl5epjYnFmQ0lGEw9fft4Kf/ONkepJ5Zs5CMv2cPewJFdBnZtx2nRn1KW64YA23tS7B7luAS4n2fJTQL1vxCWfICmr6ggTnXdWFL+Bw7+1jiXXnBqt9AYdrbm3mgze209mm8onTZhKPHiyg7a0k/rJhC0IIAmGPYbZpdZA7rptEIqbiOmSvIQOC1PVlmGcWgCrQ3ogTWN6G0pEvgH1ohvhQMNorl40rob2xc9j9xZURHjzwm6PWrqOFkYz8v5xdc1Sgjjms0/p46fdd/zBf+9t7mFzey8p1fi5Yes0ozzdoS1RzXdWOUd/vzd4yftY0L5t4Ix1wkvl/hj1tgxQMBfj/iUl0fYOSEDAv1MG8UG7SlekKLimt43fNMynIMGuu/+oBvn9TTY7B0QMu77m5lw/P2ka5noTp5FTnerpzAs4QJ63AkgqvRKs5K+LF6n1BN2vgAaYFepgW6CEeVdiZ9h6MIVxsqQwx8j7F5aTCFh7q8CinQoB6WjfOqlEY+i4D5/Eyz1IU28yadIAZahevq2W094Y8FUudTIRLQLFG8iuVxNdPQTboXqWXBCAkLip3PnEG6ggaRqkvt2C818G8qAhUgVJmsVM3+MLOpSiRASWhhMA+N0LPiSGmbmqi4/+xd97hcVRXG//dmdkq7apXS3KRLXcbjDHFxmB6J0AgCSUhJHESQv0SCEkgEEICKSQhEEKAwJcCoYROKKaDjY2Ne7ds2XKTrC6tts/M/f6Y1WpXu6tiywT4eJ+Hop079965M3PumVPeU2vDfLIbkFzy/QYu+G4LNodEVWHCoQG+e+J4ohGwO60qWjPmdnPO5S2sX+bmd/9TScA3MPmcVFV85QVcdNhkrrxjN8ee1cE7z+dx740VhMPEzFI91muBCEpcf2rG9afm5H7SjGSzS879VhPvv5RHQ709TYvBI13/gxuUAkwAACAASURBVOmtvbGz3+PZeR+zhjUM+EwIecU+CRMnMEg60wQIK7+FX13wRuyXDzEbbwe8kP8oin18xnOl1Mkzbx5SOcF/No1PzqxUAFWCnvoIRlujXHzYRL7xkwaOP69jULbg4cRAY9kVSZXDhyIkp+fXAzD7tC6uv3snD/+yjIaddorKonz1+kZOurCX/rWveGuOupKI1nqgS0F9KJsGl4sSWxBDF4SDAoerjwB3mYydbkXAqIpF1JbaFzRG+rygCiiT/JiLB+FIj2nt6hQftR4PW/CCAUaLA6U8nPoMKKAc1g3jVYxFuZBgxjBMFcPsFYRJg0jYO34i3kc2oW0MEj47D3VzCLNQQz8ii7QPm1dl6+xKbAEfbrrJLdTparPxg3PHUj4mzAXfbaakIhL7chVUVge5+le7GTUhxA0XVLNtnSu2KfcJu3TZrApUxA6pCr6TxqMXZRPd5MWbtwPTUPjjD0cQDfepxTtEaDaT0RNDXHRtE3t3OGioP7AYeakpcdK0odgqFEWgODSi4fQhQX/6hNjZh4LPhJA3Q++xPwK+B+mFWRe0nYVZ8CyKbXLa87rbX8Q9xHDKlmiyKUMIEOMCyM1uSIywiBq4lu+mpcHOH66vZM4ZndgdnxzTGlgEYOsD+fy8ajGlCYUxjjmzk2POzKwR9V3vmZ4mXmwblcKRI7DWq8AWQhEwsiaEr0NDKEZ8LaS05J4np39TWVSq/LulOmUesqAnOSuTYDIR5WHEmBDCqyNsJIVZKiPCpCtRIASggsw2cB7aQXhpXnJ4pmZab18oUbha/9UrcwmPKsTxXjPakoDlzNEE0qHg/3UFZkWyOVFKgdmh4FhlGee7O1X+8498VBW2rney+LUcvnXzXmwOiR6FbevdPPXnIrK8BrVr3H0EdOyqbSpdZ07EsX4fkepChKagF2bHIwzCE0t54akygr6mtOf3Rc8KSwBNITShGNuezjglw4y5Pr55817u/N5IliwYXPSL7FlohaTMW6kpmFl2RGco3lIMYuOx2TXmnHcE1/3125ydlfo1X3NENS7X4J3TnxR86oW8GVkLHd88eAO0XopZ9DqKmqZAgpk5fjqT1n20t8FijkwISVTGBS02v83ZYEiEbuJatjNeLi0cVAalwUszvaLXF4YBHc0aWV4Tpzu9cIwaEJA2vGo0o5NREwbXlK854K+L2d4Gxji72BrMiRcrcSo6czx7uap8LY6YaUOzQZZXZ+cWJ958ncIyHUUhrRNaWkoxIVMlIlV+sXMmO8KpceQDrZdySDeiKpw5s1mFNMFHScf1EoPz5q7m6fcSggN0BeHqRIYylDB02EDSW5UqKiFk4LqzAf+9I1Payy1uAqNqcGhLqagOsavWhR5jtNQ0g0f/UByzlVtY+J+8fq87UpVL1rt1hKaVY5SnmaNpsmTDCGTX4Ei8BBAtcGPkughPKYtXXxL+CO66Rm77+yoWL/Cw9M2hca93njEJx842q/qUsKxFoQklHGrfgk2DirERXn00n/42cofb2jTHzRjDNffPx+Vy8br5FLd/+S4WPrMUu8vBAxt+T+mI/oukfFLxqXa8Sn03suUEhvZBlhndhsob7VU0R11MyWrlCM8+K/tPKJD3NxRHb+1LM/gidF6PlKnUBv2ZVTp1OxdtOokuwx7PuLRLnXHv7yZ3mcqaRVFE2EgpMXfnE1uZPtufROcNEAkJDAN+//1Kzv92M+MP7T/e+e3ncvnzzeUE/VZd2HlfaOeqO/bEnaBgKY4SkbEwycFA2FR4umUMr7aPxCZMzi2o49S8+kwlNzOiR7h36TZWdBfy8L7JbA95U+L83UqUUluAxoibroWF0JKmUHlOFHVOB/1H2VprpCIz1w+WEptiEm50YC7JAylR9/lQ2/xEJpameVgk3ufWoPoiKIHkfAhpE/geHoUs0OLXiwTjxSIwJceuf531i7OQST4OiSvL4Kyvt/DUn0utCCEGyDbt+R9F0D13DJHxfWobR3S8/9mArcnXTy/JMDWFrrOnYOTEtGEBakcQdIOcUlD/uREzMPhMchMIHhqjfNZUlGAEtSNI9vtbOerodvJL4Myrb+Ku+c9Rtzo9B86v37iFkD9E6ehiRk/55GfcZ8Jn1vEqO29kuAS8KWFTIJ97G6ZwtKeRKkcXr7VXcox3L7sjHiaI7yKLP0IIBTO6CTq/D6S+nwPtmTlahEcnvM4TzWNZ1FWGv04S+Es3u5dG2U0Upc+r53AZfOEbLRSWReMcLoljbl7lIqdQx+0xeOC2cn7xaB12h0RRrdC2xOSoVYuy+P33K5Ocou88n0c0onDjn3pfAgHDmtU7GDgUk4uKt3JR8db4bwOtZbrNVAh4o30EN9cfSdoEJCRXla3hvKJtGKaCppg8XzCG3z58PGYfv4Aojg6QLtg7QQNhSZ3kcPj4pKJSRRTrUNWN2Ook+7060A1LyKdB11lTQYLaFST7zVq0tkDvkCEDKWNRMAYYb8S0ckXQUGfvI+Ctqw76VVbXldB1XA2uVXtQfCFEPxWU4j2Ykuz3t9NZkI1RGPNpGCZKIILW1J3mYjND0U1ynlmDXpKNkePCtKsEZ420io8s2YErlKmOVeKDYBl99Fw3nedOTaqUpezw4X1nG0LA6sVFHH/RHMbNnMNfVh7DheXzaW9MLqr+h0U/Z/JREwY9/08rPtWavNk4iX5zpoeIqAkRqeJQTDQhiZpW+bRbdx5Ol+7gdzOvxemcgtn6NYguTtvHwLQCdqSMIAS0Nal8+EYOm1e6ePvZvIQYZUvQazaTP75cS8WYcNzZ2Ld/w7DMFaGAYPtGF/fdXM6Xr26ielKQPXUOCsujjKyxbLU3fmkMK99P/Ry22U0eW7kBb17/ZdOkhO6QRpZTj33h9Ns8CRED6mrdPKFO5O1gJV8qrGV+2fqM/PdSwnp/DtWu7ni8e7o2fecQMFRuqZ/F+12pWbVSwqXFm/hG6cakPoOGyt8XT+fBN2eRKLTE6ADKFH8/Jp1UXTiLKH5DI+2FSaDdxPOtnShBS0PvmjeW6Lii2ICJjUV80iJikPvocpSoERd3UoHg1BJCR1YnnCEp+/tCwsF0se6S7lkjCR9aAV4d9+5tOP/VOigRLYHwuCL8c8aAAmpbAM+Czaj+IdYu7nN17V+Zgem1fFTeZ9Zga05fYk9RTUxD4Mo2QAoKR0RYdcxxlpc98QGQEm9I57zsfI678GimHjMxqbqblJK9dY0UjMjH6fx0k5/1RX+a/Ke8xuvwZgRpAtyKEQ+/sykSu2Lyo4oVrPfn8vD2tVZDPTP9qaU5Zw7J8xm9wsWbZ3DaRW18+9a9PLxoE4VlvS+N26tz7DntjBgdToom6dHMe4R9jz3a6ZaMmxZg1IQQt10+mq8dOYnb548i4OtdI4t6Ns112yRtTb0fdf3t+7e9MI9Tf3kJ+hD2VinhqQ2j+Obq43i1YyQhU6PDcBBOwxvf87Xyams5L7RV4zc0jDRf8FLC7rCbkKkQNhVMaQnrtzsqWNxVgl2kbgxCwMXFtSmbhks1+MqstfSNdJF+MYCimnpwbFYHZxfVxYu4920uMOMCHsD79lay3qpFdIchO9obhpkwaakIwuMLkS6B5xIn3kkSxQT36n04Nu7rbdsdiT1D6W+gkecCIVGP6sCY5ADn4HZpAThqm8l5bi05T67C/e7WIQt4gHFTAzzw9iaOO6cDzwirdGJ8bjnODFQHksOP7+KFbWt5bMVGnqtdR/SCiVZIXBoto8uhcfW932Ta3Ekp5TuFEIyoLvvMCfiB8OkW8q6zhrW7TLwvbjXKbG8jL+6N0eDbpvffUdEHoE5JeyiRo0SL7QWuLElugc53fmZlt2p2yZe+18QNf9yN0z34Ly3NBl++qinhb0nN9F7n8KSZfpQ0CVtSWlzkPYiaSkZBf/WJS+jaYfD6v/OHxO3y93Vj0aucSJt1/W91VKRtF5IKl24+gRnedq4dsZpCexgjlrzUM96+iIuLN53EJZtP5sINp3B/w2T+2jiR7207lp/vmomOSpXDlzaU0qOlF04eW0+UTQyKRKkJZXQ6Z8JqfyHrA/npv3KkRFuUrK1KYqX9PE5EWTS9fLapRGbn4vvf0ew5fwSNV1bhGmUdcn20E5AII0LB2i3kFqbbfSWKHfRSL6IwCioYh7oxRjpIE7ma5mwLQjcIHDWK8KSyIRtJ7U6Tb/10L6PGh/nxn+t58sPVOGy9cw1NK0+ueBWH4Nrf7MHhkrhjJTC3NBamXycx0Kb8/xOfaiEvvLeAUjJwwzQYioBSgBsrV2CjCzO8GHJuytzYdhiKmoNS9AyiZDOoycIsV0sfraJqMOsEK4VfUeD481I5zxORyVRSPCKC3WnidBv85C87kpKHLr5uHw6XTCKTcrgMLrp2H3anxdse1hXebKkglIYwSwgo9vqRThsv/r0w4xom/i4lREwFtiU7EH2GnR9sn02XbouPFTUFN20/kkuLt5CvhXDHNO6e4uedbSpBv+C6ujnsCHsIS40mPYt/NY/nr42T2BDIw6noXFi4lTtGfYBDpAq8LYH0MfFb/TGWzN6rRbjTm4kyRtpg8tPKpfxvzVu8MuVFvle2hmy1h3NAgt/E8WBvUpCMRYP4YyX1ZFRAuiQp1cQ8QkN6VHAo6CV2nF9wWSazkI73iZXkPfQRco2P9UuzqRofRFFNhCpBBTNPo/O3VahndEJO1Lr/isB/xwj06a5+BbYU1hdA22Wz6LjoMKKjC4hUF2A6VcyYV1zSG2HkdBuoqkSzmaiaCUgqqkP89KEdHDK7t8aAosBlc3rZG42ibHwn1GC6bEkafdXkCvInLwf3N8D5FShaxLxpNRkmK+O1Yj9HLz7VjlchHFD4PLLpaNIFK/dof30jUvoeH4i5UQhQhcm3y9ZB169Qip7DzH8B2i4kOT4/C6LrMBungDrWejCN5pS+MsEwoKA0wi8eq6N4RK9QbGnQiEYEpVXpN4hEaDb4xo/3Mu/8dnLyktdkxJgIf/xPLY/cWcqGZVnkFel8+aomjvtCR3w9DEPw0dKRnHxmqklKSmjzOzl+7l6uvH7HoAqmiFhw9GXjt3A3RyW1W9FdzBfWn8aPKpdzXM4edFOyrSWfY0Z9iK2PsBMCPLkG28Me9oazUvnfY2Oel7eVK0asB2lVrwoYyXbz3++Zzh+r38euGKjCKkAUlSormopx2aIEozZQTcSYIMJlpg7QD/635k1qXJ1WKUh0Li7ewhn5O7hu22wO87RwXvFmvl86nraQjeCVxeiHWWUC5T4D1piw0wk5upWBa8bGU0zINhAlCV8gLoWWMi8KQYvIrCOU6Elg52Y30g7+G8rwlhh88ejdHO5ZTEMki3/ljWNrJNfirncqhOYXk331zoQathKbw0SagvLRYcZMD7HezKPLNJGGJbSzFtahSIPomEKEL0KWx8l3fvZljpnTzNJn76S10caEGQGmHeXv93m9/JgVLNlxLKu3B0E3iZbnEKopwrW6l6/ppn9dh6K6wPvD+G93XnUuC+bfZWlfPQPENIu/XPvFAe/T/zd8qh2vPTB9fwD//SQK+qYuN9985BxOm1rLt4/7KK2g16PWs2EbHFUNUVNgUxwopWt6xzZ94LsXgo8Med6JkNJyxOYXGXFHn5QQCQtuvWwU7c027n6pNiXbc6hjvLp2LO9sGs2dF7ye0RRhyvRfzlJCi8+N2xEhyzE0h7cehV/WzWAreWwJWtEgAhOPGuXfE1+luS0bkJTldOOypy+EIk1Y4S/khu1H4zfT3TRrbf42bgHjs3zcs3sKj7aMp6+AHuts5/LSjdS4OtkW9FIf8nBx0Rbeaq7klo/moHtNXN4QJ+bu4pWOUbFiHv0L+TGODh6d8EbaaKuGiIv5tcdTYAtxZGs9/whNxszpdc5KEwgqGK/mMHvUOlZ6RhKot7hrREUIZVwgOYxTNylc3U705swcK5F5HlzXevjHIW+RrUZxKCaGhIipcvvmGbwZqoxrN/ZHWnA+14HbHuWeVzbjcEJBqY6hCwxd8MyDhfzjd6WERuQhK8G5yFIKIhMKmfP9M7nm/GMpzs3G9D0E/l/3u04pKFxId8TLWy8v5y+X3YceiGACxnQXwTPLKMwdyb0XfYnRZckx6lJKjvr2H4j0KAOm5HffOZvjZqRWSgvoYR7bsZC2sJ/zRlSRHf4n3aFl7A3n4fZ8mcNKv5Riv/+04TNPUAYgQ28gO66CmMPrkge+yJbGAo6pqefWL7yJx5nKv77oFS8z5vpwZQ28BsmRHNmIklg4ZfdD0D3EB3vA/pPRUG/nxxeN5s+vbxmSjT4dOgMOavcVJLFbDmZuUUNhU0MhE8uasWlDm0PPtZkSdKmwM5zN/9TNZpTTx/UVK6l0+GnrdpCbFc4YtaNHLZOW39A4Y/2Z8aSpNKORo4R5bdpLmCacsO6cGPFZb6cuJcqPKpaDEEzNaqXYFuAnO45kSVdpnGkTCaowMAZw7ksT0OEK1wa+OmVD2rkHDZV5a88FrBKGRhSwJ++iMgq2ZWEq5oXZE85CYBJJvMbEjkMmIx/ZQceLmaOhwufncsVNuzi3aHvSV9ETTdXc12AxioJ1U0SHQd7VdZx2Vivfu30Poo9PMxQQ/O3XpTzzQBH2Egh4nSgNUXImujjlf8LsbM3ha2f/jLFlXmgewF+VBGeSwgRw1i1303j4vuSYCr/CU3OvY1Tx0JORXm9Yw02rH0cCxbYAZ+fX8c+mCYSkikCSJaKMcXbREM3GYxvB3bO+yYq27Tyw9Q2QkpkF1Vw86hhGeYqT+jUMg93BNspcOdjVQWqJBxGf2Tj5RAjnicjC16DlRBo7s9nenIcpFXa15aBlIIN69V/5TJ9tEToN2H/Sy9uNbPs65P0Ruv8wPPMXmQV9QUmUkF+hrclG+agD42dVFZPRRe0DN+yDQNjG1IqmQfCoW/9NimyjJ/beIhAb6+ri+UmvxNuYEiKGmlbASwl6VGDooGqSbE3ne+VruWfPNKKkI9QSccpnRYHHq17lyk1z2O3MRUEyytnFjyuXMzmrdw1ebqtiSVdpMqeQwKIBHuB6hQLSEKzQ8rkYgZbmWWrXe4WAIZQ+/PA9/Uj0I+3sCPdEfqhIIDsSQg8Kwg4NYQIqTNywl90vptZ4jfclJHkNPmbnNCYJeL+hxQR8IneSQPEKpt+h8O2T9qCk2dOcbsmXrmrimQeLCEzIJnRtMV8s3caVlYtRhRXbHjHeIRx8HId9LkTeSzOrLCCx7q8TCpb2rothsK2xjcaZloAXIsLR2U3sjGSzi1y+uuAvvHfJjzNccXpEDZ2bVj+BjD2BhoSH9vUWh5cIuqWDNcFCAJr1Vs5691ck3vQ9e5bz/J7l/Y4zwpXHE3Ou+UQI+3T4zAh5AEWrwsx9hFDLdXHnYl1zPhv3FjG5ogmHlqz52OySh35exvd+sWfQJps4oouRkeUgNJAHTozdk7iUDkJAKKhy+/yR/ObpbbjcZtqXcSBICTbVwGnLUHAzA4SAHHfm1P5EhCXsCOUyytmFKRWiUiFbTV2fJLs9UJgdyNj/tg1OisvDON3SikEHxrk62BDMo68UFpgcmt3rB3Gj47+wmYqSRi79RwdnjN+TEsL+QuvoZAGfODGs+HOZ+ENfmIIPXphI0+gVFNuDSUqFlPBgQx/+8XS7eaJ9uWd4AX6HExzgDEVwRCMU+ivJz6lkN++mnwuSgpIo99y3npagGxKokjYG8tCEJNxnHzI0lbbxOdj7oT/Pybc2FdktmZzXztz8BnZHsuPFXTTFpLPxa2gjl6OG/wbddwNhEEWQ9yCKfSKm0Q3RjWCbhKJaiVX3v7SYB19eYikH2VHU4+Hv4xdQk1BHQALXbjkq3bT6xQt7ltOboQatGYq19w2dHSr2BNu5cOHdPHfs9UM+9+PApzq6Jh0U52xGTnyf7IQY4Gv/dTpvbhhDRLfiqXtw+iVtvP1sHi//swBzf+pyd1xjfWcPA3reb91MfgijEVjxfjYBn8qurU5CgcGHifWNctENBU010fZjg8gkgHvG6LHl/2XvVC7bciI/r5/JMl8REZk+L6hv36qSOeLpg5dz2NnuYovfy7kbTuOevdPYECyIkU4ln+QQJpeUbInP6S8/K8PQBY0XlHO/fzptUSc9NbDjc88wL2lY+/cPKlZiTxf33tOmwYGMqMx/7TQ2BfMImwqRWBiqCfy4agX3jX2HUltMkxUkX+wgIkJCTjududkcP+swNmxVMLyOPvOWgGTyrG7uebWW/GKD6lwf0YTnKUeLkF7/l+RokX6nsXe7HdOuEJ3rYXMwj+vrZnPJphOZs/o8jl39BX6wfTZNpoPfPnkLm4MFmEXLUUo3o5QsRLFPBEBRs1Gch8cF/POL1/HAf5b0LoVdcmvVYmpcXfFgiJ6oyLtr0icf9gdfNIhLSfQdDebF2T/b/N5gO0HjIFRBGQZ85oQ8gKo6uP3yL+G0K9hUk0DEzh0vzePSBy8gEOnV2A471sdF1+7jo3ey0ffr/oQZroxbIcAwBa+vqyYcVekO2QkGFLZvcvHbay1OjXnntpPlMTNGC6XrswfbmnIJ60r6UOQDnHfPfwVwRkE9d45axK0jlzE3p4Ei2+AWNl2EU8/LH3YpXBM6gctqT0zi/JFxh6jEpUTxqBF+UvURk9yWKaZVd7L5zJHo1Q6ix3loU91ctPlk/tIwhQ3+XEKmStQUnJS7C2eacEt0gXg3h2Nce7mr+oOYkJa9m4MOhBXMWjeYgsYdeXyz9ngu3nQSIVO1HNjCSqqb5m7lgXFvo0V0tA/9iDZrvHwtxHlFtRzhbSRXHbjO6rItO+nwBeg8/xBCU8pwFKt4Zns4/kaTZ7au53fP1ZFXZPXdM3YPqh2d5KlhUra1kEQs6eap5mrCRupmGwoIHr6jlMoJYczjsghLjYC0YaBioBCWGkt8pVyx41h2tPqxt/yC1r2Hs6NzSb/XcteTfb5G2jROyd+T0i5u1mvMEDqZAeeU9N0IDy52+1sHbvRfwGfKXJOIWROqePqWr/PswrU0tHYxa0IVJ80oxq5Xg+9uIIoQEb50ZTMXmDFN1EwvbPpHj8XZCQylGHIq6przueM/x/Knt45kQlkzDe3Z7HhTxyn3YcvVOfuylv12vI4t6UibOToYDJbHXggY6+pibMKn9oGgZ0zf+YWE29IQiMWgIvlj9XtMdHckFQsJmirr8kuQv5I9/nh8hp1/NE/gH80TAMkohw+3EiVsxBLAFOJtjWVe1LDKy6vGc9ns1Tw3+RV+sWkmz28aj3SZyCY7cqczVkJQIhzWAh+a3YImzKQNVVMkWYrOsc3bWfRRDuqWEEdeEWSmp5m79h6acDXJIZ99sSG0k4jNg9roI3DUKELqSJw2nZcDklf+OIs/XPQy0ysbU87rCRd2EUV0GEinYsWPqgLnX1tY+YbKovZxrDq9iFurluJQTQwd9u2x8eZTecw+rYtrTtvD/S0Onmkdm9o/goipsNHhobUji5G5e2np/C6G5yPUDLZFf7ivAqAMmS6jP+SqLdxQsZKf75yZGnJ7EDAy65PJUvmZFfIAZflerjh7dvKPjsuQ7ouQ+3ozUgerGWeGhKzLwf8IVgmg/YPHGcYwFRo7PTR2xjhmpkB4Sjk/PuMdxk4dGmd+X+GcKSxyQGdq/F+xLw7DWrOPK+pscVc5/Qk+Exjt8CULeEPl2ZYxSKFARh5+YdEPSwldYGz0IHINiCjIXXZs9T7QTZYUjeCy2asBmF7UzPOvTcfstFmZQi4DURKCqEBUW/d+hN0fT+RKhB2d4kkGYVsuMkvlA18e7/oq0lxbZkEfyQ6BPQvD64gFxygEIr0OpWseO5075r/EUXnJTnIhLCfxVSPW8NOzypGlNqRHRd0aAhOiR2QhDZPJ7lYcsaxoVYPykVEu/UFvFvVZBTuShHyZ3c+15as4wttE2FR4rWgkVZ52FAHZapjatteYUHh62mvJctrpDqZ+6WUinhsybBM5Lb+RNd11PNc2BnkQBf2UnMrPHa+fJMjuvw1/p/6H2R+nTSLKcrsZV9LCxr3FGAkk5dVFrZwzY9Og++n53Dbl8NAFSwQ/3j6LU/N3McrRxeat2YzT2qkaF0ZLeIIOVuWq6ypWsaK7mJfaR9FtpH+Rugx7rH6EVdpuWXcxTzTHYqZVAeF+diYhkCGg1Y5sUlCbu/G+vNzSdIEdbxlcv+NQNhRPRjcV1MIopgSlKmwV3jaxCleogCHZ1J2LP6ri1gzWBfJZ3FVKlqpjf7eT136m4fHVgyKInOol+o1CizRpsFDAlmMSjdiT7CrVRa2MKW6nucvN71YewWPz/oNdJH+6KQImZHUQPXkC9jd9iB0R9MlO/D8bAUhwKfy5YSqdhp3vla9PP37C4+RRIjxS8yYeJYKqgFMxOLdsW9xEZCKIGJmLx9xw4Tx++rfXkn77qK6YmWOa0rZXSrf0szCpENpYdPtsJrrrea3DIGAOnO+wPzi6sIY/zLxs2PsdLhxQnLwQ4jfAWUAE2AZ8XUrZIYQYBWwEeoqfLpFSfmeg/g4kTn4oMNuvhfDL/bRIdeh9XGj2ubnyn2eyt92LqphEDJVfXfAac8btHJQA7bmd722pYt2uYr557EpAYtdSee972utRK1M23XFDwkuto7hjd0IIbsikcuk+7vnC0jhzpTNr8L6C/UHQUAmYGpdtOYHmaGqhWwXJ4Z59lNiCbAzmURtMpi8Qu0LICkfGXcimG4TfK8DsVMj7+3KUPuXfpKbQefYUjKJsVMXAHBW2GCr7BGbIqIB1Th4/5xke8U3ivc4RhKWKfVU3jp/t6y0CAkiHIHKCh9CVg6HmiGn3EnINDy3/sUJhHJrOXV96helVjZhSoAhJrS+Xmrw2nEqvkK8LenmwcSKr/YW0RZwQNsm6cTf+X1RAdrI5xano3DV6EYd5krO1A7rCd2qPY3MoP7ahmpxTUMcPKlalmD1hIQAAIABJREFUda6HTBWzcCHZ9mQzxlXL/sqy1jqEEEzpHsvKNzswYw9ucU4Wz373tzhSOMRuQyn98sCrpO9C+h+C6Fqw1XDPrnKe3ttIyJTYhUHETBfkaiHdo2H6FAip4NVRFEm23YFUIGBYdBUjXPncO/NyyrPyU0/+GHHQkqGEECcDb0kpdSHErwCklD+MCfmXpJTpWboy4GMT8tGd0HpihqMqovhDpO8+0FeCOhVCT3Gg9vahQEqoa86jsTObaRWNeFzpI3gMCc+2jGF9oICLijcz1tmV0s9tzx/LxUevZVxJ+uzIvhz1fbLEkcC2kJdf7jwMl2pwbM4egqbGq42VtJ/TzCGzfJRURJh/6x6yvanP0kDa/VC0f13CWx2V/LT+iH5a9cyht1On0Lmx/CNur5+JrqX5eJWWAJUhgfKkJPuZbSjRPg4MAdPOiHDCVVFeXlPDklIPSkHmZCQnUQyhxJ3EWdfvQlufam6TNkHX42PANfAOmaVE8Jt2FAQT1kxhzfZGrj3pA754+Dqctt65hA2F3eEsyh0BXKrBhkAe82uPQ5cJeQVSQrcBTgVsfceWnJS7ix9WWtwyphTYhMHde6bxXGt10g1zKjoXFW1hftmG5B4krNYvZkblLfHfPmzZwlXLHultFOvHpdh49+SfDXj9A0FGNyPbvgzSCoiQqIRMuHbbMaz2W7Hw0mJmiI1v/SPbBEQVlFKdeAx9RGB86IUOm8UnZAoYHSBrjEHYFU75IHh89tWM8aSvDfBx4KAlQ0kpFyT8uQT4VBBHKLYqTPKANElBnl8iFC8i50YAzH0zSS/gD562LwRUF7dTXdx/0pIuFR5rrqFLtzHZ3Uq1syueCNTTz83nvEtrd+a6lH0dzYlsj4piXeU4VxcPjnuHKAoOYWAi+HJRLf+8rpSdK+ycdnFrWgHf038mDNW8owmrfGL/SI15LrH7OSa/kbsci7imbm5SGylB6gKhgXBJ1DE+hCah774qIU/xc+rUncwdv4PXWqr4VdOMjLMIYUt6PJTGDKG2KtBlDErI+00bSIlQFO6/+gJm/889nH3oxiQBD+BQTSqdfv7dPIbzirbz8/qZ6H3pJoVI0eATDvJmRwVdhp1ILBzUrkhW+gtTbljI1HiieRzfKu2T7Svg0Iofxf+8/YMneaFzZe/YCQiaUV7ctZyzKg8bcA36g/T9AmRvwpXAwKXA9RUruGTzydZvSqq/Q+RL4lFyUiIRGB95oD3md+kJQ93pJDSpLe0z+72lf+WVE35yQPM/WBhOm/zlwBMJf48WQqwEuoCbpJTvpztJCDEfmA9QVfXxld9SSj/EbLkI9J4vBw28d6K4z463McNLQQ5PpMhwwpCWgP/97unUuDq4ZeQybMJIEvA9UBUo9g7tKyRdhJEqJFqMo11BognJN67e22OO3i/sj/0+koaDvp8RANgbyeb6uqMosoUo0oL4DSsEsKeN0HrnYkx1pY2KdboNZp9u2Zfddp1Ti+t5rnMUm8PJn+lSAkEBLpl0fUaNE7HEn1TW0SzQ8N9UCsWDfQ0FCElxIIrTqbHwd1eitD6QtqUmTO5tmM6fG6cSzVSEVlgUzulug4nCh77BaaYBU8Pok+0rRAFCWP4TKSUvdKykv9CZ3258IUXInzH664Sa/KDBpFMnc88Tt6Q9N47IypSfDAlNERcKJjZhxugc+kBY/4orHWGg1U4Kwb3HJNMD3xrx83rdOuZU1uAacmblwcWAT5cQ4g0g3d3+iZTy+Vibn2C9Go/GjjUAVVLKViHEYcBzQojJUqZKTCnlA8ADYJlr9u8y9g9K4WP9N9A393PQBooHZLDnzR7OqfWLBe0V3LP3EASSpye9ilPpv6LTUDAYZsnE38RBcramQ8hUeb51dJojqSaaRESlygp/MQoyIZTO0uhSYvNzNUJfzcf5zzaISIS0BHzN9CBzTu91ItqEySn5u6hv9BCSNtAtDdBcn4UyOZV9MXRJAdkrAphRiXF4FkaZjcj5ecg8dcgL6HdFqd3TQnWJzlJ/Pod5mpNs4qaENf4CTERKScO+GI57V2wLoCbkDwgBFDwdP772/Y39Cvh0OMl+AehWPIxEsPGpdRz/7pd5q/HxzCcp2WCG43926ja+XTuPfVEXJiK22WWeQ3x6dlAmdWOuy05ur/c3f8lPNj8Km+AE13TumDew/+DjwoBCXkqZyXgNgBDiMuBM4AQZM/BLKcNY+yFSyuVCiG1ADXDwDe7DCcdx4Pt5+mPaBETBE7GNQEW2Dm8Bk/6wzl9Im+7kwsJaxH/JQQyWlqRw8KJqemBKiEiFVd0FPLwvtSanholHjdBuZDZLAX1ipXvMbakTj5yfjz7Jhf3VLioiXXz1gj2ccHZ7Eje/IiQXFG3Fq0X4z9YKVmytwtibhVIdSqvpmaMd+H5fATka0iEsgjKV/Vg4QRd2mju7uWPbH2nXZ/BwzVs4FBOnYhA2LSqJX+/ObEoabuyLuvlp/eEcktXC+RWTEbm/RiTQZjbtbIEBQsivm3AGYGn9Vx19Buhueu5NzwopTQZ3/ujP3HjHd9N34v4qdP+ZHvrv3+85hN3hLPQY25nZzz1PhBDAyBAiqCK3JTj5fYol6PsS9CU5teDN0Gqe3DiaCyf25zv6+HBA8RBCiFOBG4CzpZSBhN+LhBBq7P/HAOOAugMZ678BRasEW7qXRYD3NoRQEbZJCNt4cF06pL57bN/74/eel7uLb5SsZ4yzC1XsZ4bTMCBT2eXhhiJAIGnTnXjVaNxsBOAQOkd49nHH6CU4FR2Rpq7AYF7svjAnughdV8LWH47l1jHzOGfTGTzZXJ3kr7ApkjML6vlGwTaMDR4I2Czu90z1C0Y5kXkauFXLwTBkAW9RFyBhVHke6wIO9kQ8XLjxVP7aOJG3O8r5274JXLjxFOpCOUPs+0AgeL1jJPPGPoWS97skAQ9QM7PaMnP0fdhjL4BDqHyhahYAi3bezq71mcvzLXjgncyzyJrPLvMoIqaCL2znrY6KuIBPnOugrkgDZVwA5YgO1FNaUOa2I8ozZG+nuY93b35pUON8HDhQm/y9gAN4PcbH3BMqORe4TQgRxbq935FSZia//iQj7zHw3QbBp4EoqFWQ8xsUezLplJJzM8HwbmzG2ylfppk03f4KmvSHw7JbmZHdSkSqH3u1s5731JCCfREnI5zB/dqohgqHIjk9fyfH5ezhsaYaXm2vwiZMzinYzheLtqEJyeMTXuMf+8bzfOtoq2QgCg6hk6VGadPTafmDWT2BiaBFd3Hf3qn4DDvfKN0YPyqlFfbaYzKSrTZkfhQxrBkoPZuUpYlKFM5b0ktv3Wk4+EfThD7th7axJT6j+/NlVuLModDlTXusasIIxv7BQe05kXhmXU/35bYcnjvRCnLYF+qkkmcx5ai0cxdABgohAJ7ZtYxfbSggXzudijqDSIV6YGqsXSJKrEI9wqkjD/MNbl2EIOrQeWXPSk4bcejA7Q8yPjN88p8ELN92CpNd9dgT4pMPtikjHbXvcPadqV/dtGopSwm6FCzxldJl2Dgxdzd2kT4mfzjntSfsptge6EvLDkBjxMUjjRYp1nUVq1jYWcbtuw4nZB645HUpUV6b8iJ2xWRTIJc13QVEXgnxh7ozrR3bbqIe3wr24bon/fkbMgnyoX+5ZB5+4AdMAE8dcx1vN27gnzveJ2rqzCmawM1TzsOh2Tn3lkeob+oAdMTMbkS+jhKRPHT45Uwb05s9+9yuZRyvXMZ915Xy5r9TGUZBMvOSWdzx9xvSzmPuglsImVYUk9lkA0OglET+OwxdUuLWnLxz0gDO4mHC/ws++f82zOgmxjt3Jgl4OPhOyYPdf6IOkDhWrLwnHYadb22ZR5vuJGyq3LX7EA73NHFL5VLc2tBMSWm56GObSCLRVjhW8MGW4dpL7UFujMV4CwFzcxooafBTH0nUNPdv4SSCVt1JrhrmLw2TWewrRU4RaKs60PNzLUqEbg0lf3iI6/qfZyYBL3ErDgLmEFj3YvvCnKLx5NiyWN+xC900KHHmEGj1s0/vwnAJNFWjNeqLn6YJlQdmzedHK/9FbXcvZ86CxjW8vW89JzfPiQl4AA35US4SiRQQPuIBVjeMYWLxV2loDXHvw0spOrGE6+7axaKXcwgFkqWz6RIZBbwpzbiAB1CKoxi1TsgTuNwRgqYt7XkHDULEE6b+2/hcyA8X2r+VxJ2SiIOtzR8sDObz/be7DqUx4o7bPgOmnUWdZfxaOYxbRy7rt/++bLtCkBIGKgSEDJVuUyFHjbAtlMNLbSO5qmzNgGu6N+Ki2BZkfu1xMQE/CBvaAJAS3EqUhxonsdhXZv2oAIeEUTw+crtMuvL1YVOkB5oL9L0My6zTK+BjiV5Rgdxnh9wIIqs3vNOMgNzqRtY7UaIackouN3/nLJQ0dsQPmjZz7Yq/Jf2mS4P5H96PkcDb3oOoNHhxz3Kgr6lMIKWkuXYtcye9xL6dD3LBXV9BNxTuef0oHrr8WZ7asJ7/vaOEt5/NQ3NICkdr3P3OMxnXQhEKIoH5H0AdF0IGBSe6dvOSf9TH5kPqgZbJOfMx45Mxi88CzH3UBnNSmB4/C8XjM8lC04Q9kSz0Po+RjspbHRWD6ren78ebqzO2cyomZ647k6NXf5FLN5/ESLuvX476Dt1GwNTI1yKoAr5fsYoCrU+2aSxGXOpWFqT0C+SAkaiSHDXMuRtO59Hm8UnXwUQV90u7yD+iFZGRL2j4HgZpgrnBhdxns+YvY9mcKRCYTTaM1/IxV2VjvpWPudiL0uzguLzJmAsKkbVuiKiYUvLu2jpO+dGDace8Z8uraX/XMbGLDItXmlmbbfe7cKs6q7aUoghrM9qyr5CvPXg+b28Zw+lXBbjmrQ6+tfCLKQK+I+znyqUPc+yCWzntrV/y0u7lzCuZnHr1LslO7aj/ShTaBVVDL3RyMPC5TX6YYDbW0BRxYldMHMLApRoEDRUDgVvR0yYqDRf+W18KUlp0vu26g+u3z06K6LAJg/enP5vSPtM8/bqKWzXSHo+YgnM2nEnAUAlLjRcnvUihLX2lKhkLt3QkmM10KagLevnqlpNS2hpv5UFQRVVM5EwfSnHmIjD9mqdDJjnnbaP7P2OQQmSgtt1/W7mpAw12zGY72E1EQRTqnch9jpjyLiFPR5uTTAhmhsF8tTDNuJLCHDctnenzOwoLTVpbBYqqcOLMsXRPaObD9tq0bR0xLv50dXfNFg1zUW7a8d+4/hFy3WF++uzxvLxmfMq5YCKmd+MarTM5t4pZ+dUsbNrMvmAHLbovpfW84kl0RAOsbN8R/63GU8YjR36XOa//9KCL+cTne3bheH4/82sHecRefG6T/ziglFJsb6TbUNkYyEURlnOydY+HE2rqEYo8aIL4v2UKEgLcqoFTCfCn6nc5a8OZ6FJBxeQYb2qhcCEyC/r+ErrsiuSJqS280DqKhS9spU1RKJqWvm3A0HCqyfZwTUgqHd2MdXawNZRAXKYD3dYrYFcNcl3dNElHvwlh6XQiKcH2fjd2l40xDS3UlheTKtBlLBkrVdjFek8/KJaAN9/LteYqYxE224Bp3ahTAhjvW76AuUV7uGLcB4xw+tkVzubPDVNYuC7zF1ImAQ+SlhbL7GPokteNZYiWqMWymQaGFGSpUcKGmnoduTqoMhYV0xOnDkdPryMUc+wUZvvRFAO9J5vZlNh2tcLpUeQIlYgJK9q2s6Jtu3V6SIAr9Tl6u2kDbxx/ExLY3LWXsZ4S8h0WZffJZdN5rWF1xrU4UEgJwqdw1cyTuaDqSJzaJyfr9XNzzXAh76+ASrZqMMPTSo29kxI9ym9fOpbL/3ouhrl/MfGfBijCKi1356gPKLH5KbCF+J+K1Bcq0/X3CP7+NiuvXELrb7bScHuQ91/IIRRM39gkfblBXQoKbL0mGynB3GiVoROYeJ1h/n30ixye3RgP88uExBwHKYGwYPxHXqbMmUDT933khYMIZMxEIFExubRoM7Oy96H1iePXhImtz28p4eS7nBBQE9LsY+GU67KRDgNlmo/jJ27jF+e9wdisLlyqQY27kztGL2Z8dib+IwFuvZ/rjI3lNqwwwgwCXmCiCUkg7thM7k/RQDmlFUYGICuKWhhGndvO0lEevrDhdE5fewZHTNnRa+KKGuQ8uwZbVjOyQgGb9WAIAbLJhvFqATKkZnxWHt2+kBy7m1mFY+MCHuC2aRcyPXdkhms9MEgd5BY3T516DZeOmfuJEvDwuSY/bFBs4zCLl0P3nyD0HHe8NJUF68dimCpnTN9C1FDR0hSS+KxAEXCUt5F/TViAKkwcSnrhkZEeYYD+pZQce+YGXv7bWJ66r5gNH2Vx5S93M2ZSss3Xqejopkgqpg1gV0w2BnIBiSIl5mYX7r0q0h4hyxHl3ktewqHC5aWbWFtXgCpIEFx95tKhgM8GThOzwYG2281vXvgWix9byKr3N2Ccv4fCYx1kHa1y5EldnF25E10KVEawvLuIRN2qL3GYlHCEp5GLirdQaAuxqKuMf3x0GB2GQlV+B5fPXc7UEfvY2ZbDwwtnsKHLRX5lFzdWv4fLlvwF41RM/n7Oi3w4ZQS/eGlebyEaANVEjAsg13pI3mOsdRPTfCgVsezdfm6ORKQtgq7sjuB8pAVpQuiqYpQpfhStm3K7n3K7n4+6SzARtBlOrm86iqNm5fLeYh/OdQ2o7QGCxxdYDJkxmN0K5rIcMAREMuumufZUGmoAIQQPHvlt7t+8gIe3v5P5goYAa4MHc72Hu876IiO9RcPS73DjcyE/jFAUN3ivx4wsJBCxYZoCTMnRZdtw2Q9cwEdNwd5IFgW2ENnqcIXoDR/UmPkmHQ7UbyAETD/aj81hEA2rrF+axTVn1PCbp7dSWB4lv1hH0JNIKpPGCxoqL7WO5JmJr+JWrXYdNU5W7izD6wpzaFUDamxTyLeFOT1/Jy+3pWp9Gia6EJBjYizMBgUUU2VCVQmKCCPHPMZja9djU00WLSvhkR/k8eTIarxenctKNjPO1cX88o280V7BnbtnEDCTNT4p4UuFtXy3fB2u2DpWOro5/Ss7+dETJ3P3xS/j0HQ0VVJZ0MnMUXtZ0FLJqaX1ST6IRCgCjqzew9NX/ouvP3QuW3bn4djRghr1Y3oFkUMMzFW5lk1fCsg2UGZ1Ity9uQ5D/gKVEscTbYRPzcGY4Y5/WpkIGiJZKEJy95j3uLbuGAwUIlLlg+LtXHHtibx82mZ8hkT2iY81dzrBlIiyCGgm0iQ5szhmHbtwAGfnd8afTHPEF4v6sZCtOvAboUR6tT4dJ6L3mCYlx0T93Hj1T8j3ZA1mZf4r+NzxOswwTRNav0Jzx0Yuuu8CjKd3cP116znpgjbSUZn3oEu34dUyO/0A1nbnc8P2o/Cbdk7Oq+fGihXxePVPMobLMSwlfOu4GnbV9obkCUVSUhHhR/fVU3NIMCmDOF4hCyvKKYU2PQO2Bz3cufswNgTy4nzwYH0llNoCbA96MV4tgCydMqWQB689n4a6c5lY3hin/dUNQVu3i/t3jOPmaauTrt+UsLy7iKu2HZs0rlPReXXKiyn+iYih0NiZRUWuLyVDerBrKyWsbSjg+8eOQugGIiyRLoGZq+G7oxLpsCGcJsLR297c7gQBSpWl0QuR6mdIq+ZHTeuQLb0NzqVE+dXIxSxor+SljtFJxw75SYTtK+vpengkssQWj4IyV2YhyqKIoghCS9h4eiI3BZxfdAQ3zjxn4MUAwkaUWl8j5a5c8h0eokaQFdsv4IG95WwJ5qIJk6hUmexuZaW/kDwliFOVNEazEFg+nm+WbuOkmidQ1PSZvh8nPne8fkwwfX8H/+0AFHlgwQ3/4M3qXJ6+v5h557SjJRAb9b6cgrc7yljvz+N75eszvrBSwnh3O49PXMD3ts7lxNzdsbjfg7tJ76+ATleI5MAnA62NqfbOzhaNsdOCKQKwZ1yVXiK1SBgc7qkgAmBsSztMqd3P78Ys5M5dM3incwSmFFQ5fPygYhW/qD8M2aGhHNmJoiu8cMnXeXPpM8wu35fE666pkmxXhKvGb+StjaN5culUukIOjp9Yx1eOWMshWS1U2rvYFfHQIyjHOjvR+9LbAnbVpDyNgB8KhIAppa0owRG9/OhhMKUD23t+9C96U9orlSGMt3KhKhR/VlORRtAPwMsjAJ+0cYp3V4qQd55dQtTZgizuLVUmBIjKCCKvly4i/pUhrOvACZWBgcN2e+BQbUzJrYz/bVNdzBrzd2YU/JrtHe9TH85GNzWW+TyU2AOckrubQ72S1dGzCEZbqMk/mRG5ZyI+IbHw/eFzIT9MMI1AXMD3QAg44fwO6jY4+fVVVVz7291oNomqSQI+hbyiPKCF+xqm0hJxcUX5+ozmTyHALiSaiPL76oVkK3pSFujBwlAFtC4F24Jexrs7D0iD73uulLD0LQ8BX6INWzLzuC5WLfQMOE7Pcc0GW9c0M+6Ed/EFVpDl+0rSmgcNlfWBPCa52/n5qKVEYqyOTqGzNZTDXj07KZv1qAU34TUj3JXrYao92cnptus89PoRPLlsKqGoZd/f3u3hybZq5hxSh5QxFTSGdt2BLQ3hnClhYyCfiVntKQl3Q1nfcFAB03IHB48sJjSrEoojKNNC6Z87DdSTO9Id6Rk9/c8G/UoWXSpMdLWzMZDXq5LHnN2rjuwmdEhZSteiMJr+WiXgBNmmUTkir5+5Dgyh5GPLu5OaPIsyF+BUfTdEV4FaDLaZHPUpEOp98bmQHy60fTPjoct+2MhZo6ezZkkWp365jZyCKJNnBcgragGgIZKFLhVeah3JWQX1/b64ioB8LdxvMtB/E35D49u18zglt54bKlaiDqXGRwxSwramHCryu3FoBqYUfPS+hzuvqExshSvb5OQvtbF5VRbhoII7e2AaBUWBh7aUsZyfEzQiVDjO4raRHzHO1QCovN4xkTvqa7hqxFrOL9pGVCoIYG80ixvqjk7bZ5ewMX/H8Tw2fgF6SGV1WzGHFDbhMnUe/XC6VQ+2uhPhtPIxu4BXOkdBPPpGMsuzjzPzd1hmArMPjYOp8lDjROZ6Gji/pJfMdSibqJTw6uP56JOcBH5UhpmjoahWeYeBaggM2aLbjxx0Cp0T83ZhSKwyjgkUvUgIdQQgJ9XhnTH8VrF8CebKbGZdWJly3oFCaBWgDf4L4ZOIz4X8AcIMrYCOK4D0JJtCgM0OV/9mJ6d9pT3tC1Vm97Mr7OG3e2ZQaAtxlHdf0vmfJmSpOiGp8VrHSE7K383MPsWg02FnwMUIVzAuGx7/cAp3vTYHgBxXiEDEjqpHmHfiIla/qhAJCybODHDlL3dTNS7E2Km1GNGBJZGUllZccWSEd5qCgMAl/NSHBNlKNuXZR3D2hFuZXmjjsrv+xb/crUwcvZeOVi/rugtxHB7ALnQifemMhZWmf+mKU9CdWHbiDnDsFHByG0pCkXSbMNClEjO1CcY4OvjT2PdwKgZOxWBb0EvA1KhxW6YbBfjjnql82F3G9o48zsivRzcUnDYdBZkxtDERpoQPukr587uj8f+8DFzKkFKyhvwMKlbAQVIGoJQUaEG+VrKZMwu2880tx2OkqOsCvFr6zziRWuAFrL3B2OJkxDwFp+1j5qf5lOBzx+sBwGycAXQP3M7AcmBl0HDe7ijn1vpZ8YzBHDXEbG8D80vXUWwPJ70rpoT2qAO3qscjMHoQdzSa7JcGPRzY4M/j8toTAMnZ+dv5cdWKAc8JGQofdRdz/fajOSN/BxN83Xy0voq3N43BkCoOLUqhJ8C/r3gMTSWFojmxGPlgBJIhSalolawpZtEeKOHZteexoaGUmooivnjMNApzsvjW4vtZ3VlPOlNF34gPGQFiAn6cq4MfVSynw7Bza/0sQqZGRCoU24LcNXoh49yWVr0pkMt3tx5LrhYhRw2zPZQTL1lntmnYF2dTntfFyZNruWzOKjQ1+f3tKx8jpsLPdh7Omx0V4DctZ2g66s6DgSR2O5jiaqXa3cUKX1HMF9HPOYkX0VOdpu/vVnozOBR+O+MS5hYn03//f8LnjteDALP9JgYj4MF68fsTPvNy9zLb+xxPt4yhwu6nxt0JEkoc4V6TZSxdX5cKDzRO4ttl61OEvFBKQB2Hqi/cz6saOnqEiikhLBX+sHe6NZdYHdh07SXJSp5TNTnK28ii6c/ERef5k7YQiGjc9MwJTK/cx8VHrsLWx+nWg8EIdynhjY4R3Lt3Gl8r2cg5+TvSkqH9X3vnHR5XdSbu97t3imbUq2VbLnLFDXDHdAwGU02AXwIhAcIPCBAIYUkCBDa7GxaWAKElWbJAwgIJNRAgptr0ajDgblzkKsu2mtVHU+49+8e9kmakUS8ji/s+jx7due18c2bmu+d85ysW9WT6t3Hp/HtAG4/kvtq8wHZYqsbq2MwBLf3QWnfaCj7X3cCfJrxHneHm6q3HxfiVl4Z9XFN0HP+c9ioezWSSrwqfFmFvKJm9tLjlqQionUk0RtxsK8vm0Q8yGJNTzaJpsbV4IkooDqaQ42pka2M6/10ynbUNOdbB5AF+8rf6UNYFclgXyOn2degCWwOQqlsjfRe2yxTg01iUP+NbreA7w1HyPSX4XJdP7cro0qPBBXlti2dFe6h4xcSLyc2j7YLFrmPALAItG9LuQvOMxzxwXdxC1P1B9EBNATURL1sDVv4ar5gsztrV5prW9uYm4q0x+D0R7rvgzT6Rs8HUeaViHPeO+5jR3toOcwnFjIbNIlTD80jy91BKcXXe0/y1eL5tsOn4g226x7nZ23CJyauVY9qaKOzaox/X5HNCRgmawJ2Fn/GzoqMxlRBUuvVgLPdYka82EVPn1hdPIsX7GnML91gJy0x4qGgqz4SmdLOH4rzvRNGeABN8lp98SRjckJkbJNtvctuEA4z1V2IGC9C8xwysrAcJjpLvBQn9UehzIOthNbDbAAAgAElEQVSRtilhI1sHTITo964LpOshzsku4rnyiXw3dwuHJlfEnB80NIoa05ji78hjI/79e4qhrARnt2yfx52Fn5LchSCyNu0GnoHk74GxE8xKHpnwDldsXRhTpEiFpN1CIeN91Xg1k4pwUozffYuMwoFIiwI/NLmCF6a8xrKq0SytHMuOulQaVrRKlQwYps4vnl3M9xesRuVEeM+d174ZpB3aqxcwKNEEVeABFNeOWsXi7F1Wj4SA0DuY7tlo2U8nVsZByMHnDzRo6KQycX8geeA6DPCDsRJKD8EsOwUzErW4KYmLvEvSDY5J38s1I1Zz9Yj1QIsSaTB09oX9rKrLHlBlogFJmuK+8Z/i07o2xbEKlcQ7ogMm01Kq+PjwFyn0tNhtxAPD3A0sztzJ0Wkl6MpEGda91tdn0WhqzEstxafFD3ib7rc8rQKGzoGwhzcPjObZsglsDmRwjNpHm1KlNo2mi8fKJ/N45SR2B7um4KNrCzeZuga9go8iVQ9xStautvOo8JeYgfZzzn9bcUbyPSTgeh29bh5u7wD+QFQpREpj9xnboeIUGGYvcKZcCVVXDpBAsZgKysM+tkelHI4ooaQxmRrDw/PlEwgrDVMVdSn1cl/MlGIWV7t4jangr88VsPY1H0cefYDFF4ZIyapGXKNQ+igwiqgLwfZQOk2+f9eMWMN3c7danjMKIqbG1c+extYCD/9wjeOCvM0ckbaXCUnVbAlkxNjldVGsqM3nhfJxvHFgrL3Q2iLtcn0kZIShonWBawU5IbSJrXLlt0P8xel2ola7gVciXDV8HbNSytgdTOXJ0kl8E8jq1T074qi0fe2HANY/Ab5z+q3tgxFnJN9D9pdU84M5s9m23pv47JKqDjPwGgBa0kJIOjvuaaaC58vG8esdc6kIewmaWp8WNTGUMMZbzXeyi2g0NEKmlYuxIKmOGSmV3DTqS87NKaI64u60zwaqT+O1o2uwcE4Z65b7efy3+Vx+tJuKDaejjP1I5oMgGdxdMr/5/AWp+zg3pwivZpKsR0hxRUhzh7h/yVuoD7Ko+OcILnp2CZ+WjuCewo/50bAN5LkamgtZNJhu/rj3UF6unGB7WMUqXRFBX1ADnlaumzroUxraKO72+i76nNGeGjL0xjZtdRdB8er0pZybU8QkfzXHZxTz0MT3OTJtb6/u21mbRpzIYIB2Kqd8q3GUfA/JKciioUG49jSrEHHCFX2oJeGSlnEX+H/S5pS7imfxx72H8lbVGM5YfwaXbl7IBRtPZmegcxNPTGpdG9M2a9Qb1ujVJYoJ/lom+mrQxURQeDSzeVHVrxtM9VfyyL6pVEY6fjgWB5MJmv379eyo/WEjrfJ5wYBOVYXOk3d7UHX3I64JSN4H6J6ZNCnIs3O2tUnMpgkke8NMG7kfwhp79mdy494FnLJ+CQ/tO5TSiL975eg00ObUgN+wAoAyQ+hHViEZbU1Qnc1+0vQgvx//AbVG71PiKuCzmmHNi+m6gE8z+GXBV7RJudH6C9RDPjowvP2ZoP+CXt9/qNGrX5GI/LuI7BGRVfbfaVHHbhaRrSKySURO6b2og4u0rFSOO28Bmu7ls2WDIAOdp8VF1jAM/lA8jMf3Teb1ytE0mjpl4SReqxxDo2mZCRRCUWMGO0Op3L47rnttM0rB1VuPZdmBkWwNpFIbcWEqaDR1lBL8dgbEaE8gt9aOx4xucE7OdrJcrSo7uReD7zLAUjw37ViA0c7Xs68eqB0pw+g2jIjGp2+mQeO79nVebpxxdfNxXzsFT5SCJDv9rzauvQIdXZdVyw3jXlTOCzc8ifvYKqSHxcLPzNrB9mBqH2U9Em7bNZfaSGwgUpYrSKarVem/PjL+1ygvL351SNvvgWsqWrKj5FvTFzb5+5RS90TvEJGpwPnANGAEsFxEJinVeRXNg4nrH7kSX5oPpQbOoyUukobmOxWAulCARe/ejqFMhGkkaQb37jmcK/PX4RaDUBvvDomtlhTv9gL3j/8Qj6iY6kg+LX65vpY7t6XJPNTmOnMT4r8M1fgUqBBZriDXFR3DfxV+SrIWRhOFBuwPJZHnacDbR+sg7clfVhI7yvX5TZCWXOU+t5cjcybxSflmlh0YxQx/RZu4BU1XrN07zHqR3HFfdRWF8JNtxzPSU0dxKIWemFtEFDduP6qdEoXdRxfFJ7X5nJK5O0pOaDD6LwL1rreOodx9HFfP3QhmI/gvQPOd1vmF30L6a+F1CfCMUioIbBeRrcA84NN+ai8heLxufvqHywhVVkPwfxIkRTrktviSX77iYQzbLqnQCJgaoHiydDIRFb/uaIarsXlRLt5ip1LEFAERga2BNJ4qm4SOyc8LVrWbz7w1QVOP7+ViHgDXDNCGg7GDH+Vv5Pqiozlr/elM8FnJzoqDyZyUWcyto79se30f0hgQnv1DXvNrr8/kzB9Vgf/imPPun3MJX1ds48avH+f0rJ1M8lXh1yOETcFA4z+LZxNZVAVvpkG5C3KCcSKmFF7RSHL5qA43tDnWVokL5REfnl4EQzxXNoFQnEIfPUUBZpSNPGhqLK8qaI7U7Q+0ZJMLjroSLTml39oYKvTFo/waEVkjIn8RkaY0cCOB3VHnFNv72iAiV4jIShFZWVbWeZ6TwYgr46cJdEGrQcya5ldF9fvjnCOUhX2M8NTjou1k6qrh64io+Ao+Hp/VDOOyzQt5o3I0H9WMiHuOUlAV8VAd8VBnuKg3XARNjVV12Yz0tlZmgHs2IoJkPYahT2W0N8SvRq0l29XIjsZUdgdTOCNrJzcWdJ4moacYyvLlX/pyLu8vzcCXYuDxmhx1ai1Lrp6NJF8CQMQ0eKV4JVeueIRHt73LL6ady76kB7hj9zyWVozhmbKJXLTpJN6pHgUa6KfWMHNeNhluywUzqpfwieK1E37FX464khSX5SvvFgOvRPjFyK94/pDXOULfj7HRh7kzCWXr9hAuu4B2940ubWdzvSNk6sxOKaXO/ow/q8nnzl2z+rSNGBScsGQE2Y6C7xKdPs5FZDmQH+fQLcBDwG1Y37TbgN8Bl3ZHAKXUw8DDYOWu6c61gwVNc2N6zoLQKwloXUHwA3CN7fAsA43TR53N33a+x4FwU7ymcElBEosySzu8NqY1Bb/ZNafZBfBAJInlB0ZxYmZxTLGLiBJu3L6ADYEs5iTvJ0WP4NfC3NgUrRuDDun/AcDSvXt4cNNMGg0rTP2M4TO5POPX+PUIni7OFnpKZdjL9duO5orFG7h7/s8p27mLCYdqjJg0H3GNBsBUJj/78nHWVO2k0bB83tdV7SYvKY2d9SNYXhX70Gt6aK6uLQYgXQ+jlEaWR+eCUVNZUnghmqaT6knm7RP/lWdW/ISCzLXMTClvXsy985BPuGZlFquK8mF9MvoxVUiqEdcTp2u055nSM59VA43vbzqZMd5aSsN+ysI+Kw1DqRvJDENS97JlxptJxrjCavCDiU50a1fpVMkrpU7qyo1E5BFgqf1yDxCd97PA3jdk0bLuwdy3HLBGqQMZDatIav7ZjvHnsLOhPO55FxYu5KIJi9jTUEFZsI5paSNx6y7M0Peg8qyO27Dfz/bGVCqjojMB7tg9m4qIl/NyiqxMio3p3FM8kzV2zpTP6poUn+LLulwemfQeRY0ZrKnPJtuby4ljbyJdz+Pjsk3cveEVGs2WgKFX967m6iyzjYI3IqDZA9K+6ucsd5AnJ7+NaOlohyyABW1Lya0o38raql3NCh4gYITYVR+/z1tTbVi+7uGgh8Vjzkez34Qy62kMBVgy8r3mxdomktwGPz5+JVc9cRYYCuPLVFzHdy1quFsE7emcR1B24d2u9m2d4WF9gxUgaJa6MT9PQ/JCSH47eeDjoeyog+jfjmr7SJqdWchhWWO6eFOHXhnmRGS4UqrJIfY7wDp7+xXgKRG5F2vhdSLweW/aOijIehoqzwO68cXuC1wto8eH5l7GGe//FrPVNP7y8QvR7dSUI/3ZjPS3ROxqnkMwcaFUJK7cIUNDNIUo+LQmelKnSNPDNJgu/nvvoTy8byqm0jHbL33CnnAqS9afTqreyHBvI6IUf97zR+6adQV/3vpejIIHaDTDvFY5mvNytsXItuz5TJY/n8FVt5UwemIQl7v3yr7ZGyjzz+2e83nFVgJGqM3+7k5BAyrE4rdvJ9WtUxoKoKFYnL6Tm0fH900Yk91UkESgxoUKCuJRVst98WUzFdrKerSQIliYC3UutCn1KL17t1dhwfw8DQwNGRFsuwQR75qmt1Hp4c753+PBtW9RopeimzqnZcxm5Og0Xt3zFS7R+P7Yo1kyam6P3+a3kd6uvtwlIodjfcd3AD8GUEqtF5HngA1Y6bJ+MtQ8a+Kheaaghq1E1f8N6u7HSqrR33gRs8XckuNL44NF/8Yd615iZeU2srwp/Ov0c5mYNrzj26T/Dqm+rp3psnDe16dyav4O9oQsd9Fj0vbw84JVZLqCmAhLK8Zwf8nhHSj4JoRD/JVsDmSyNeDFVIImijvXPEBpJL6Mj+2fydnZ23FHZbU88dwqlj2bxQ1nTyRQr3PCdyq58Q+7O3WL7FRh5XyG5mo/WjPTk4xHcxEye58FLqBCBEIAgomwvGYUP2cV7lbrJqaCIjMVbUEV5voUqNWt4W2bN9OL6FUB86gUK4Haaheq0o3K8CC5YZRbQUjAqzpV2mp/lFeS3rU+l6Cgv5PPHZeeygkTJ7BwYtsEa5eOP6EHb8oBeqnklVI/7ODY7cDtvbn/wYiID0m5DNN/AVRdD6GP6E1ayE5/JKKBa2LMLo/u4d8P+2632tF8p2K6D0PKFwOxYfJ/fP9I9q4ayePzUiDZ4NDUcm4b+3mMDf6MzJ149uv85455aAWt/KOjSNeCbG3MaM6dD4CCnaE0Jnj2URXJbDMqDuFDy/sCqv8FwiuAIG6P4q4Xivji7TS++iCFzLwIkbBVoCUeSkG1kUSGezio7fFP0qd1qOD3NFSSpPc+gKiF2A82pFw8WTqZi/I2xbhjBpXOI6XTkNww+jEHML5OtUfxseiYKKRnrpFN9VQB/fD6ltG1ZqU5JqShAkCa0VxnNS5Gy3tSJV4kv/OBzlmZR/DT/1pEWnJSp+c6dB8nd00/oWnJkPUwYNlbVeWFENnQ7ft0PArygGsq4p7RMyFboblGQP4azMAyqP8joEPKDRw5P5+nV7yE8V4m+Ax+dOlHeCR2tJnkMjhl8jbue28B9ak6Wnr8idsh/gOsbWib3K3R1PGoCF7NRdCMNCv6JN3N1RNPxu1Kg+xHUSqEKj8TjO3oOhxxcg1HnFwTc6/WQTLFQT//s/dQTin8BccNm4FZ+yzU/5oYI4s2ArL/Gldm0zS5efXTfFj6DS7ROrTNmA0CYQ3xG1ZSsW7G/zy2fwo1EQ8XD9tEhivI1kA6D5YcyoaGLMvFVQP98Nq41xroCCbRI/omZa3qdNR+N9roIOLt3Lgk0nwLxAUq2UBt8kNDGEa2b46UvBAoy+tFFXthWh3Kq9qt6nTe6CP4xdQzO5XHoec4laEGEHPfbCD+D7T7uMB3PpL6c0Tzd356L1lfUsId/3yLHXsP8MyFf2Vkatv3URd0c9nmE9geTmt3Wn9kagmr6nNpMNsGysz1lPLTwy/ioW3bWF9dTF5SGv9//EIW5k+POU+pCCrwKjQ8aoeVng/eoxDXMBAfKvQBn+//kAe21bKt0cXwpAx+NuV0jh8WW1jCDG+G0BfgmYnmjj1WGw6wu6GCkBHmys8faV3wr12UwipkHRZIsn5bPTGZW2nPuo6K0Jypsqk9oygJtc0PEYGQZqVDcJvoJxxoV9F3NHM0q3XEZ8adRURjbPKhtiRb/ZBkos2paY7OFbH8ti8dv5BThh/GmJTcbrxLh/boqDKUo+QHEDO8GSrOoT1bfdc9cjQk5zXENa4vxesyZtW/YAReRW9V+SkQ0Tll7ZmEOpjPj/JUUxZOjsnCCJCkRbghZz1nzXwZ6dAe0L+YyuTW1c/y9r61vQr779pn2YENvanxTu6hFBDQMN7NhNwg+py6ZhOL8UZOjPkEAE0h4xvQ7MRm3ZE9XmW+9q5XB1xWkRMDZGTI8rSxr1u28BbSPYMgFcgQoiMl7yQoG0A09yTIWwNpvwHfRZD5F8j9xMoTT1dHbi7IeChhCh5AUn6CSFJMBstAyMUT+yZ3qOABGkwPvx79BV6J4BYDQZEkEeZ4Szls+KwBUfAR0+BAqK45MrgJQ5lc9fmfWd5LBQ9dfVi3f5Lq+HDsiUpZo/W9SdYMAqDGBXHKL2IKqtQDjVqXslU2N2OCub/rn42WFUE/rA59Vh3asFDMPX+77uUu38eh9zg2+QFG0zTwnx+zT2U+iKo8v0s51sn9Ak1P7ChIXOMxMh/ni83XMSO1gso6H//78Uxey8pDUts3bLgwOCa9hIWZe5ieXMlbB0axtiaLEZ563qkdSU7Guf0qt1KKR7e+zRPbPyCiTFyic8WEhfxw3HHURRq56OM/UByo7FcZukpXTTyigfKADAuh9nsxv05Fm1ODcpsQNx2vQnwmqlxHshTKH99e3nx2k01/WxJqfQrq0BoYG+rwms5kX166jt+YBi4tQdXmv2U4Sn4QIJ5ZqJRboe4/OzoL0n+fcAXfxLqqEm4tmUft7hTUumRrsXFUAG1GPRLz27VMEkkSIUUPc3m+tfic5wmwKHM3/6wYy/v1Izkvr54U3+H9Jm9JfSXXffm/MYFihjL5/eY3+f3m3teRTSiaghQD9oPa78X4IBNtQj2kRKC6VVSsDjIuYEWi0gX3RgFztxdzvVV1yixKQR9T2ds09OyuL6cwdVjvbuLQJRwlP0jQUi7C9B4PFYtoY7hxzYCs55qjIwcDbs0qiaUXBFEjgxASCnzV7DFjS9ClaCEOTa5gXmopZ2TvIMWusRowdP6y7xDKQj6uGp3KxYf8e7/J+oOPHmRz3b5+u3/CMbHMM03U6phVbrQ5NZhfp0KV23oQKJDp9UhO14P1VARUddS9G6Rdu2JXbfYAD21Zxl2zftA1IRx6haPkBxGaezQq501UzW2W14f4IflHSPJliAweBQ8wNftYfNprNJgu60ftVVTh45ZRK1lfm8nHtcNxaybzUvfzz4qxHOHdjyhFyBSrLum+KZw+9npumXdEv8r56Ja3h7SCVybQoKPKmryVFLgU+qQGZo8Yy6qUHZgNYhUaTzUQHVSDoHzxzTTRi66WqUasBdTmEzQmekewJVgSM2NTJqgKF5IZ6VKU7OcVCU7P/S3CUfKDDHGNRbLaD6sfLLg0N7+beSbXfPUqprJSzYaVxsbgNK4eZ3KZEvZzFs+UVHDumBQWFt6CMoVlJa+Rnzqc6+ccNyByPrH9/QFpJ2EIGBuaXGitRC8yNsCYzGy+qrSDvvzKToVvmc5UjRshHF/RR5vyGzWMr1Ig3OKfccb8Kfx64SKu+PRh1lXvRhkCmsJV52H4Hi/lewIEDus8+M+tOapnoHBcKB16RSBSy8cl/6A6VMuc3CMZkz4z0SLFsOCNWzG67OV+kKEUxkY/altyrKukbiLT69HHxivwrVAGGJ+kox9tBZFFF4IpCOQxaWwOJjA/ewKL8w/nrS+2UFUX4KwFU8lJb0nvu6ehkm11pYzyZzE2JQ/V8BR7yh7gnI3HYznutT+cv6TwOK6ePOQKxiUMx0/eYUAIG0FW7H+F8kA507NmMSFzfucX9TMXfvR7ttT1X1HphKEUqsHEeCu3JR1nNH4D16K2nkJezcUVE09CK0/iDy98gjG1CtIi0KCxOHkuv1nS8+hTZVajyo6nPBjmjA1N94lKJ2lvT04dzuMLfmJ5mjn0CY6Sd+h3imvWceUXj1FnaJhKUMCRGQa3z70Tl9Y2unX1ge08suUdvLqbG6acwQh/+zljekNVYx0nv3dHv9w70aiwwng9N76rpK5wndE2/XGeN52lJ9wIQF0gyHtrigg0hlkwdQwFuR2XgeySTKFVqKprqAoFufyb+eyONC3EC5NS8rlhypnMzC7sdTsOsThK3qHf+eEH17O5wYuKiq8TTI5Og+sO/Tnvlq4nEAmxs7aUt8vWt7n+7IK5/Gr6d/pUpv0Hannqna9pMIP8w/MumrdPb59wlAJjWRYE2o7ktaww2jFtc87fMu07/Z6qVykTIpsBK3meJK5s2reGjpS8s/oxBJn3xq+IjoufnzqG3x/1435rb1/9FrYHPDEKHqwasx/WKD786Hd05lj9UvEX/HDssYxKaZu8rCfc/dy7PP3uqqg9uWiH1cHYQJ/cfzAgAtqMOswv06Js8gpEcePi4/jvxjeoN1oygp5TMG9AcrGLaOA+pN/bcegajpIfYrRW8KBYUbuDaz/+n35T9GGjEa3dRABdT7V1z8Z/8sDcS3otz7rt+1opeIvI6mS0rCBa2tBZiNWGh+CIKsxvkqFOh9QI2uR6vNtqePfif2N91W72Bao4MncSPtcQm8o4dAln5WMIcVSzgo/KE2v/X1G7s9/aHZkyrZP6q12brtcb8bxBus+jr3/W7jG1aXBEDPcl4jOtkXxYg0oP5qo0PmkoAWBaxihOHD7DUfDfYpyR/BAi3O6R7iau7R6/XvMcNUbvi2l8U7WHB795jdNHzmJ8arza8V2jIdh+Tww1lAnGRxnQGOWyWO/irQ3lvP3yLYhXIcCKxUNz8dmhc5yR/LeC/lPw/+/9e3lr35o+uVcIg7/u+IgLPn6Qm776Gz11Clhy5LT4BzSQQ6xC61bmRrtw9SByPuguar/HykDZerZkgmlHqiqazHgO30YcJT+EuG7MSfZWPKXV9x4Oqyq3szPQ1k2vL3indD0vF/fM0+q0eVMYm58Zu1NTUBhAS7UrVolYSn6vPeo/CJR9XPECGphxPltTg4ZYr5u6urr+EcxhUOMo+SHEhVMWEht80vQnfN4P0/XHtvVvyoBHt7zdo+tEhL//60X89OyjKchJJz3Viza/Gtf0+tgTkzQY7rYUftNfl4ju24FBGUC9ZuWIiWpWMiPx88brJpIda7Z6v/Kb/hXSYVDiKPkhxueL7+DWMd+nafE1GVe/KHjAqnfaj1SHG3p8raZpXHLKXF657VIWHlnYRuE1045i73hQL6TrQY5L30O63n7R8p6gVOxftCxKM1HNEw+7tGB6GLLCoEctfGsK/CYyPFa247Ict8ZvI71aeBWRZ4HJ9ssMoEopdbiIjAU2ApvsY58ppa7sTVsOXeesKTM4a0rfFPfuiCsnLuLDsm/ocq26bjI6OadP7nPyIVN5ZeNH4GuluTuq0adAhUHaWU+uNrzcMfYzQqbOTTsWsKK27UKxAJNThlMZrqc0WNP2JnHEELFG7aoStNyWfR5dw/SDgWn3tuDRXOT70zn74nm8/P4Gtm2oRZkgBY1oEwNt6uympKTg8O2jV0peKfW9pm0R+R1QHXW4SCnVf1UgHBLOxLThzMksZEv1RqrNvnfR66sI2HmTR1PwQQHFI3Zbi68aEDLB3f5DSTQwG3RwG3GfA14x2NmYSrorxAW5W9oo+cMyxvDw/CsQEZRS/Gbt33m15OuWE1TUv6ZRuwkIqGIvkhUGTDyaiysnLuIHhcd0+B5/ML7leLxF1neOdhZev630SVoDseKWdwELlVJb7JH8UqXU9O7cx0lrcPChlGL+m7+iN6P4eA6edx52AQuH991sJGKY3PvuW7xcspJIUpiMap0qrQY1wh13NK8iYG70o01raDMiBoUbA00gojRGeOrZHYotlvLGCb8iyxs7cq4I1vJmyWrKgjVETJOwMhjpy2TpxlUU72hAN3UyvH7K80rxJmtElMmFY4/ixxMXdTs1QF1dHf/Y9yWL8g8jP6X3OWkcBjf9nrtGRI4F7m1qxFby64HNQA1wq1Lqw3auvQK4AmD06NGzd+7sv6Adh77nT5uX8Zdt79BTJb8obwa/nL6ED0o3UhNuYGZmIVPSRw5IvpOnPl7J/TtfREU54ohYCp5GDZJMq1yeAM1GEut/bAqHlgyLTTx2xFVMyxjVI7mqQw2UBWsY4cvE7wQxOXSBXuWuEZHlQLzIlFuUUk1l1y8Ano46thcYrZSqEJHZwEsiMk0p1cYwqZR6GHgYrJF8Z/I4DC7eL22bbKw7LCtdy+2eCzizYHYfSdR1zpt3OC8sX8+u/RUYuSG00Y0oj0KVuK0RfMyvw5pv5OoNlBqto2bbPpAK/D3PwZPu8ZPu8Xd+ooNDF+hUySulTurouIi4gHOA5l+pUioIBO3tL0WkCJgEOLaYIcb09NEU1e1PtBg9wuN28fgvz+eJZSt56oOvaPjKAyZIfrAdvzOxFXznswxHSTsMFvrCB+4k4BulVHHTDhHJFbsoqYiMAyYC2/qgLYdBxs3Tz6a/0yb0Jyk+L1efdRQf3n0Nf7r2PIZPSoLccAd6vHMFPzdrfJ/K6ODQG/pCyZ9PrKkG4FhgjYisAv4OXKmUalumxuGgRxONP829nI6U39S0gnaPTUjO6wepuo+IMO+Q0STPCaKPa+x6XFQrUnQv9825uG+Fc3DoBb1OUKaUuiTOvheAF3p7b4eDg1nZhXy++A72NRygJhxgUvqINuc8t/0T7tm0NGafX/fw1DE/Gygxu0ReUjo76st6dG22O5nXT7yljyVycOgdThZKhz4j359JPplxj3238Ei+W3gkr+/+mjXVO7l2win4k3wDLGHnXFR4LKsqdxBSkW5dNyerkPvn/KifpHJw6DlO+T8Hh1a8tPsL7vtmKUEj0hxfGo1lflLsqi9nTEouP518KjOznLqlDonDKf/n4NANzh41l9NHzmRXfQWZnmSSXV7eKFlFebCWE/OnMzZlcKwjODh0BUfJOzjEwa25GJ86rPn1QNRGdXDoD5wslA4ODg5DGEfJOzg4OAxhHCXv4ODgMIRxlLyDg4PDEMZR8g4ODg5DmEHlJy8iZUBPcg3nAP1TUbr3DFbZBqtcMHhlGynGmrwAAAWTSURBVKxygSNbTxisckH3ZRujlMqNd2BQKfmeIiIr2wsESDSDVbbBKhcMXtkGq1zgyNYTBqtc0LeyOeYaBwcHhyGMo+QdHBwchjBDRck/nGgBOmCwyjZY5YLBK9tglQsc2XrCYJUL+lC2IWGTd3BwcHCIz1AZyTs4ODg4xMFR8g4ODg5DmINayYvI4SLymYisEpGVIjLP3i8i8qCIbBWRNSIyKwGyXSsi34jIehG5K2r/zbZcm0TklIGWK0qOG0REiUiO/Xow9Nnddp+tEZF/iEhG1LGE9puILLbb3ioiNw10+1FyjBKRd0Vkg/3dus7enyUiy0Rki/0/fvWWgZFRF5GvRWSp/bpQRFbYffesiHgSJFeGiPzd/o5tFJEFg6HfROR6+7NcJyJPi0hSn/aZUuqg/QPeAk61t08D3ovafh2r8OgRwIoBlusEYDngtV/n2f+nAqsBL1AIFAF6AvptFPAmVuBZzmDoM1uGkwGXvf1b4LeDod8A3W5zHOCxZZk60P1jyzIcmGVvpwKb7f65C7jJ3n9TU98lSMZ/AZ4CltqvnwPOt7f/BFyVILkeBy6ztz1ARqL7DRgJbAd8UX11SV/22UE9kgcUkGZvpwMl9vYS4All8RmQISLDB1Cuq4A7lVJBAKVUaZRczyilgkqp7cBWYN4AytXEfcAvIabsUaL7DKXUW0o11937DGiqAJ7ofpsHbFVKbVNKhYBnbJkGHKXUXqXUV/Z2LbARS1EswVJi2P/PToR8IlIAnA48ar8WYCHw90TKJiLpwLHAnwGUUiGlVBWDo99cgE9EXIAf2Esf9tnBruR/BtwtIruBe4Cb7f0jgd1R5xXb+waKScAx9nTrfRFpqjiRaLkQkSXAHqXU6laHEi5bKy7FmllA4mVLdPtxEZGxwExgBTBMKbXXPrQPGNbOZf3N/VgDCNN+nQ1URT28E9V3hUAZ8JhtSnpURJJJcL8ppfZg6a5dWMq9GviSPuyzQV8ZSkSWA/lxDt0CnAhcr5R6QUS+i/WUPmkQyOUCsrDMHnOB50Rk3EDI1QXZfoVlFkkIHcmmlHrZPucWIAL8bSBlO5gQkRTgBeBnSqkaa8BsoZRSIjLgvtEicgZQqpT6UkSOH+j2O8EFzAKuVUqtEJEHsMwzzSSi3+w1gCVYD6Eq4HlgcV+2MeiVvFKqXaUtIk8A19kvn8eeIgJ7sOzOTRTY+wZKrquAF5VlUPtcREyshEP9LldHsonIDKwv02pbKRQAX9kL1gmVLUrGS4AzgBPt/mOgZOuARLcfg4i4sRT835RSL9q794vIcKXUXtvMVtr+HfqNo4CzROQ0IAnLlPoAlunPZY9ME9V3xUCxUmqF/frvWEo+0f12ErBdKVUGICIvYvVjn/XZwW6uKQGOs7cXAlvs7VeAi2yPkSOA6qgp2UDwEtbiKyIyCWuRp9yW63wR8YpIITAR+HyghFJKrVVK5SmlxiqlxmJ98WcppfaR+D5DRBZjTfXPUko1RB1KaL8BXwATbY8HD3C+LdOAY9u4/wxsVErdG3XoFeBie/ti4OWBlk0pdbNSqsD+bp0PvKOUuhB4FzgvwbLtA3aLyGR714nABhLfb7uAI0TEb3+2TXL1XZ8N5EpyX/8BR2PZr1Zj2SVn2/sF+COWR8RaYM4Ay+UB/gqsA74CFkYdu8WWaxO2Z1AC+28HLd41Ce0zW4atWLbvVfbfnwZLv2F5H222ZbglgZ/Z0VgL5mui+uk0LNv321gDneVAVoK/W8fT4l0zDuuhvBVrxu1NkEyHAyvtvnsJyBwM/Qb8B/CNrS+exPIi67M+c9IaODg4OAxhDnZzjYODg4NDBzhK3sHBwWEI4yh5BwcHhyGMo+QdHBwchjCOkndwcHAYwjhK3sHBwWEI4yh5BwcHhyHM/wFFiVmt4baVpgAAAABJRU5ErkJggg==\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ }
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "import matplotlib.pyplot as plt\n",
+ "from sklearn.manifold import TSNE\n",
+ "def plot_tsne(labels,output):\n",
+ " tsne=TSNE().fit_transform(outputs)\n",
+ " plt.title('tsne result')\n",
+ " plt.scatter(tsne[:,0],tsne[:,1],marker='o',c=labels)\n",
+ " plt.savefig(\"GCS_tsne.png\")"
+ ],
+ "metadata": {
+ "id": "GCA-iK6PIxtg"
+ },
+ "execution_count": 28,
+ "outputs": []
+ }
+ ]
+}
diff --git a/recognition/MySolution/s47539934-GCN/GCN_tsne_100.png b/recognition/MySolution/s47539934-GCN/GCN_tsne_100.png
new file mode 100644
index 0000000000..c2903796eb
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/GCN_tsne_100.png differ
diff --git a/recognition/MySolution/s47539934-GCN/GCN_tsne_200.png b/recognition/MySolution/s47539934-GCN/GCN_tsne_200.png
new file mode 100644
index 0000000000..c793327c14
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/GCN_tsne_200.png differ
diff --git a/recognition/MySolution/s47539934-GCN/GCN_tsne_50.png b/recognition/MySolution/s47539934-GCN/GCN_tsne_50.png
new file mode 100644
index 0000000000..491855f840
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/GCN_tsne_50.png differ
diff --git a/recognition/MySolution/s47539934-GCN/Model.py b/recognition/MySolution/s47539934-GCN/Model.py
new file mode 100644
index 0000000000..c4827c3f22
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/Model.py
@@ -0,0 +1,81 @@
+"""
+Author: Arsh Upadhyaya, 47539934
+Code for 2 layer GCN model
+"""
+import math
+import torch.nn.init as init
+import numpy as np
+import scipy.sparse as sp
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from torch.nn.parameter import Parameter
+from torch.nn.modules.module import Module
+import torch.optim as optim
+from random import sample
+import matplotlib.pyplot as plt
+
+
+class GraphConvolution(Module):
+ '''
+ Starting of graph convolutional layer.
+ Parameters:
+ input_features: dimensions of input layer
+ output_features: dimenstions of output layer
+ use_bias: optional but good practice
+ '''
+
+ def __init__(self, in_features, out_features, use_bias=True):
+ super(GraphConvolution, self).__init__()
+ self.in_features = in_features
+ self.out_features = out_features
+ self.use_bias=use_bias
+ self.weight = Parameter(torch.FloatTensor(in_features, out_features))
+ if self.use_bias:
+ self.bias = Parameter(torch.FloatTensor(out_features))
+ else:
+ self.register_parameter('bias', None)
+ self.reset_parameters()
+ #initialize parameters
+ def reset_parameters(self):
+ self.weight = nn.init.kaiming_uniform_(self.weight)
+ if self.use_bias:
+ init.zeros_(self.bias)
+
+'''
+parameters:
+in_feature: an n-dimenstional vector
+adj_matrix: an adjacency matrix in tensor format
+'''
+ def forward(self, input, adj):
+
+ support = torch.mm(input, self.weight)
+ output = torch.sparse.mm(adj, support)
+
+ return output
+
+
+class GCN(nn.Module):
+ '''
+ A model that contains 2 layers of GCN , by creating 2 instances from GraphConvolution function
+ parameters:
+ in_feature:n dimensional vector, which is input
+ out_class: n dimensional vector, final output
+ in this case model goes 128->32->4
+ since in_feature=128(known from dataset)
+ out_class=4(since finally 4 classes)
+
+ '''
+ def __init__(self, in_feature, out_class, dropout):
+ super(GCN, self).__init__()
+
+ self.gcn_conv_1 = GraphConvolution(in_feature, 32)#32 is like the hidden layer for the overall model
+ self.gcn_conv_2 = GraphConvolution(32, out_class)
+ self.dropout = dropout
+
+ def forward(self, x, adj):
+ x = F.relu(self.gcn_conv_1(x, adj))
+ x = F.dropout(x, self.dropout, training=self.training)
+ x = self.gcn_conv_2(x, adj)
+
+ return F.log_softmax(x, dim=1)
diff --git a/recognition/MySolution/s47539934-GCN/README.md b/recognition/MySolution/s47539934-GCN/README.md
new file mode 100644
index 0000000000..dd92300640
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/README.md
@@ -0,0 +1,75 @@
+
+# GCN on Facebook.npz Dataset
+### By: Arsh Upadhyaya
+### roll_no: s4753993
+## Goal
+
+The objective is to accurately classify nodes into there respective categories(total 4)
+as per the facebook.npz dataset
+## Why GCN
+
+GCN and a conventional CNN are similar in there objectives, they both take some features
+from existing/given data and perform some operation on it, be it classification, recognition or even
+creation(like in GANs). However the difference lies in there flexibility. A CNN requires data in some
+clear format(like in images). However in a lot of real world applications, this is not the case. In fact,
+the internet itself is a graph with the websites themselves being the nodes and the edges being hyperlinks.
+Such is the case with the facebook dataset, and we have to classify the websites to certain classes.
+
+## Working of GCN
+
+GCN use graphs as objects, and to create these, they multiply features by features by weights. They use adjacency matrix to store data. This matrix is used in forward pass(function used in model) and thus forms a graph, in which adjacent nodes have information about each other. For a simple 2 layer convolutional network, like the one used in the model, each node has information of nodes within 2 edges. Hence one can Imagine just how strong a deep GCN can be, as unlike the neurons in CNN, the nodes in GCN are not bound by euclidean geometry. Especially on a bigger dataset(internet), it could be assumed there would be a lot of hyperbolic and elliptical non-euclidean connections over space, thus increasing the interconnectivity of the model.
+
+## Program Flow
+
+#load_data()
+this function is responsible for first extracting features,edges and targets, then create an adjacency matrix, and normalize that matrix.
+Further it returns features as a tensor.
+
+#GCN_model()
+Since the given data has input of first layer as 128 dim vectors, a hidden layer of 32 was used and then directly finished with out_class=4, which is the number of required categories. Alternatives, a third layer could have also been added, however the accuracy was already pretty good.
+Maybe a dropout was not necessary in hindsight as the dataset seems to small to need it.
+
+train_model()
+considered 200 epochs, and at each epoch, found difference between ouput of model and the target itself.
+Similarly for losses as well.
+Done for both training and validation set.
+
+
+## results
+### accuracy plot
+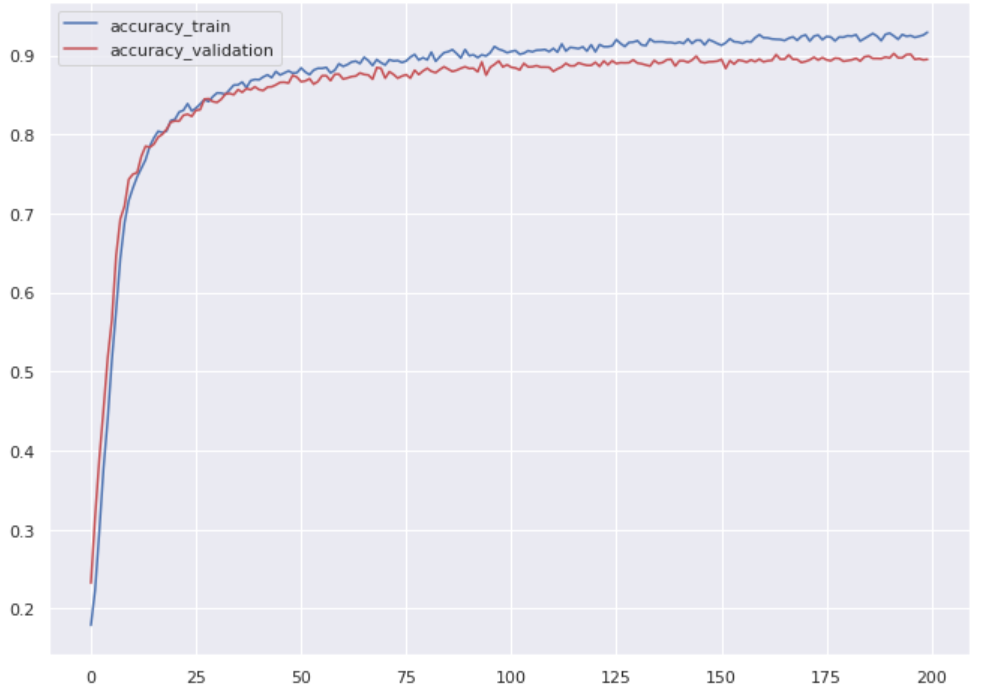 +
+we can see that training_accuracy>validation_accuracy, but only by a little bit which is a good sign.
+Reached accuracy of 0.923 on training set after 200 epochs, went as high as 0.9446 after 400 epochs.
+
+### loss plot
+
+
+we can see that training_accuracy>validation_accuracy, but only by a little bit which is a good sign.
+Reached accuracy of 0.923 on training set after 200 epochs, went as high as 0.9446 after 400 epochs.
+
+### loss plot
+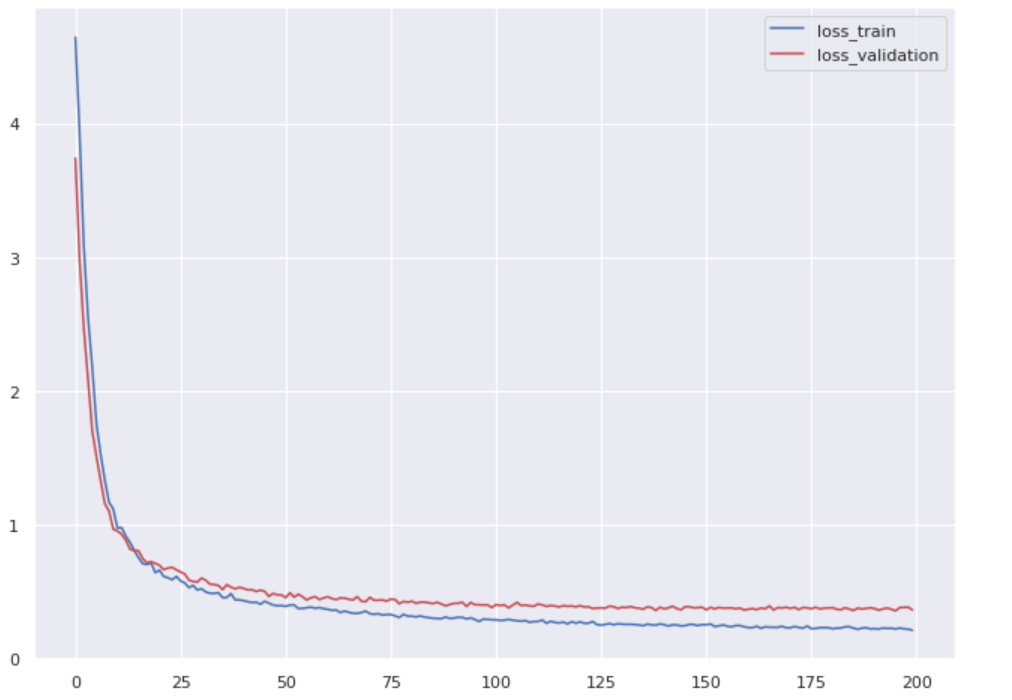 +
+### test_set
+
+
+### test_set
+ +
+The test_accuracy and test_loss is pretty similar to training and validation accuracy and losses as expected
+
+### tsne
+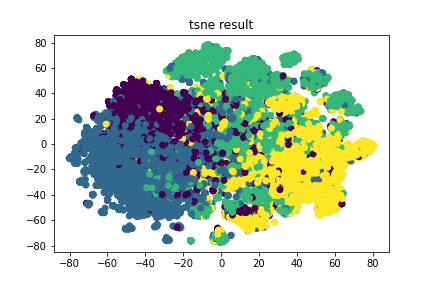
+
+After 200 epochs there is a significant accuracy, and the 4 different classification categories are very rarely overlapping
+
+## Dependancies
+1.numpy
+
+2.matplotlib
+
+3.pytorch
+
+4.python
+
+5.sklearn
+
+6.scipy
+
+## reference
+[1] https://arxiv.org/abs/1609.02907
+
+[2] https://github.com/tkipf/pygcn/tree/1600b5b748b3976413d1e307540ccc62605b4d6d/pygcn
+especially helpful in training and testing functions
diff --git a/recognition/MySolution/s47539934-GCN/loss.png b/recognition/MySolution/s47539934-GCN/loss.png
new file mode 100644
index 0000000000..96b03c15f4
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/loss.png differ
diff --git a/recognition/MySolution/s47539934-GCN/predict.py b/recognition/MySolution/s47539934-GCN/predict.py
new file mode 100644
index 0000000000..a9e5fbc493
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/predict.py
@@ -0,0 +1,29 @@
+ adj, features, labels = load_data('facebook.npz')#returns normalized adjacency matrix, tensor features and labels
+ features.shape[0]
+ num_nodes=features.shape[0]
+ #split data in semi supervised quatity, i.e train:set:test=20:20:60(since n_train
+
+The test_accuracy and test_loss is pretty similar to training and validation accuracy and losses as expected
+
+### tsne
+
+
+After 200 epochs there is a significant accuracy, and the 4 different classification categories are very rarely overlapping
+
+## Dependancies
+1.numpy
+
+2.matplotlib
+
+3.pytorch
+
+4.python
+
+5.sklearn
+
+6.scipy
+
+## reference
+[1] https://arxiv.org/abs/1609.02907
+
+[2] https://github.com/tkipf/pygcn/tree/1600b5b748b3976413d1e307540ccc62605b4d6d/pygcn
+especially helpful in training and testing functions
diff --git a/recognition/MySolution/s47539934-GCN/loss.png b/recognition/MySolution/s47539934-GCN/loss.png
new file mode 100644
index 0000000000..96b03c15f4
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/loss.png differ
diff --git a/recognition/MySolution/s47539934-GCN/predict.py b/recognition/MySolution/s47539934-GCN/predict.py
new file mode 100644
index 0000000000..a9e5fbc493
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/predict.py
@@ -0,0 +1,29 @@
+ adj, features, labels = load_data('facebook.npz')#returns normalized adjacency matrix, tensor features and labels
+ features.shape[0]
+ num_nodes=features.shape[0]
+ #split data in semi supervised quatity, i.e train:set:test=20:20:60(since n_train +
+we can see that training_accuracy>validation_accuracy, but only by a little bit which is a good sign.
+Reached accuracy of 0.923 on training set after 200 epochs, went as high as 0.9446 after 400 epochs.
+
+### loss plot
+
+
+we can see that training_accuracy>validation_accuracy, but only by a little bit which is a good sign.
+Reached accuracy of 0.923 on training set after 200 epochs, went as high as 0.9446 after 400 epochs.
+
+### loss plot
+ +
+### test_set
+
+
+### test_set
+ +
+The test_accuracy and test_loss is pretty similar to training and validation accuracy and losses as expected
+
+### tsne
+
+
+After 200 epochs there is a significant accuracy, and the 4 different classification categories are very rarely overlapping
+
+## Dependancies
+1.numpy
+
+2.matplotlib
+
+3.pytorch
+
+4.python
+
+5.sklearn
+
+6.scipy
+
+## reference
+[1] https://arxiv.org/abs/1609.02907
+
+[2] https://github.com/tkipf/pygcn/tree/1600b5b748b3976413d1e307540ccc62605b4d6d/pygcn
+especially helpful in training and testing functions
diff --git a/recognition/MySolution/s47539934-GCN/loss.png b/recognition/MySolution/s47539934-GCN/loss.png
new file mode 100644
index 0000000000..96b03c15f4
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/loss.png differ
diff --git a/recognition/MySolution/s47539934-GCN/predict.py b/recognition/MySolution/s47539934-GCN/predict.py
new file mode 100644
index 0000000000..a9e5fbc493
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/predict.py
@@ -0,0 +1,29 @@
+ adj, features, labels = load_data('facebook.npz')#returns normalized adjacency matrix, tensor features and labels
+ features.shape[0]
+ num_nodes=features.shape[0]
+ #split data in semi supervised quatity, i.e train:set:test=20:20:60(since n_train
+
+The test_accuracy and test_loss is pretty similar to training and validation accuracy and losses as expected
+
+### tsne
+
+
+After 200 epochs there is a significant accuracy, and the 4 different classification categories are very rarely overlapping
+
+## Dependancies
+1.numpy
+
+2.matplotlib
+
+3.pytorch
+
+4.python
+
+5.sklearn
+
+6.scipy
+
+## reference
+[1] https://arxiv.org/abs/1609.02907
+
+[2] https://github.com/tkipf/pygcn/tree/1600b5b748b3976413d1e307540ccc62605b4d6d/pygcn
+especially helpful in training and testing functions
diff --git a/recognition/MySolution/s47539934-GCN/loss.png b/recognition/MySolution/s47539934-GCN/loss.png
new file mode 100644
index 0000000000..96b03c15f4
Binary files /dev/null and b/recognition/MySolution/s47539934-GCN/loss.png differ
diff --git a/recognition/MySolution/s47539934-GCN/predict.py b/recognition/MySolution/s47539934-GCN/predict.py
new file mode 100644
index 0000000000..a9e5fbc493
--- /dev/null
+++ b/recognition/MySolution/s47539934-GCN/predict.py
@@ -0,0 +1,29 @@
+ adj, features, labels = load_data('facebook.npz')#returns normalized adjacency matrix, tensor features and labels
+ features.shape[0]
+ num_nodes=features.shape[0]
+ #split data in semi supervised quatity, i.e train:set:test=20:20:60(since n_train